東京科学(理系) 2025年 問題5
$(1)\ \ 関数 \ f(t)=\dfrac{t^2-1}{t^3} \ \ (t \ne 0)\ \ の増減を調べ、グラフの概形をかけ。$
$(2)\ \ 実数 \ x,\ y,\ z\ が、条件$
\[
\hspace{1em}
\left\{ \begin{array}{l}
x < y < z \\
xyz \ne 0\\
x^3y^2-x^3=x^2y^3-y^3\\
y^3z^2-y^3=y^2z^3-z^3\\
\end{array} \right.
\]
$を満たしながら動くとき、x\ が取り得る値の範囲を求めよ。$
(1)
$f(t)\ は奇関数だから \ \ x \geqq 0 \ \ を調べれば十分である。$
$f(t)=\dfrac{t^2-1}{t^3} \ \ より$
\begin{eqnarray*} f'(t) &=&\dfrac{2t \times t^3-(t^2-1) \times 3t^2}{t^6}\\ \\ &=&\dfrac{2t^2-3(t^2-1)}{t^4}\\ \\ &=&-\dfrac{t^2-3}{t^4} \end{eqnarray*} $f'(t)=0\ \ より \quad t=\sqrt{3}$
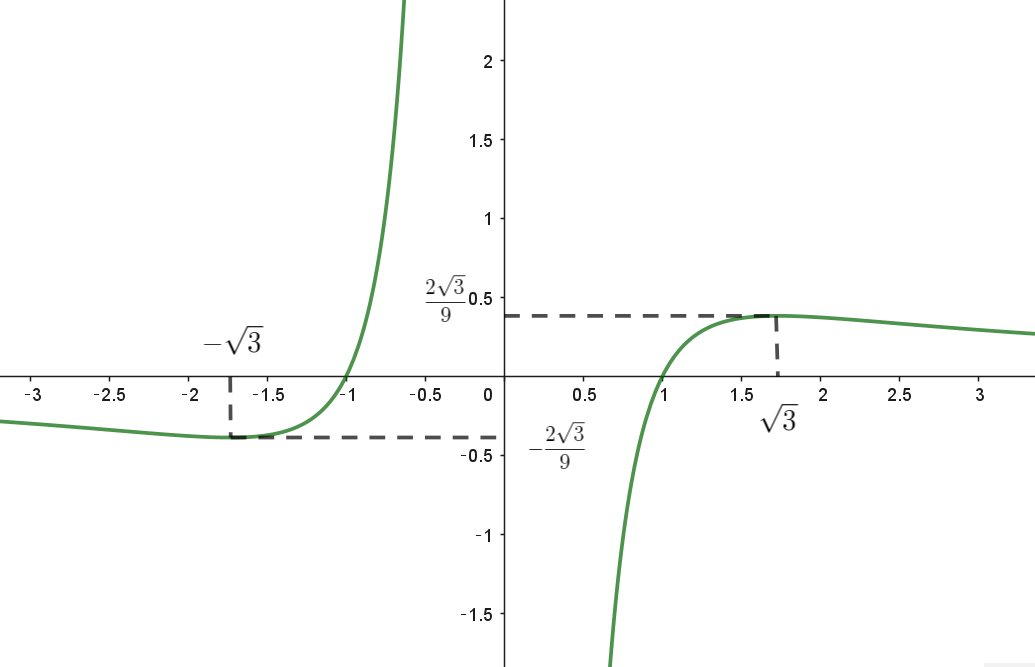
\[ \begin{array}{c||c|c|c|c|c} t & 0 & \cdots & \sqrt{3} & \cdots \\ \hline f'(t) & & + & 0 & - \\ \hline f(t) & & \nearrow & 極大 & \searrow \\ \end{array} \]
$t=\sqrt{3}\ で\ f(t)\ は極大となり、極大値は$
$f(\sqrt{3})=\dfrac{2}{3\sqrt{3}}=\dfrac{2\sqrt{3}}{9}$
$t \ \ \longrightarrow +0 \ \ のとき \ \ f(t) \longrightarrow -\infty \ \ だから \ y\ 軸は漸近線$
$t \longrightarrow +\infty \ \ のとき \ \ f(t) \longrightarrow 0 \ \ だから \ t\ 軸は漸近線$
$f(t)\ は奇関数だから グラフは原点について対称$
$グラフの概形は右図のとおり$
(2)
$x^3y^2-x^3=x^2y^3-y^3 \ \ より \quad x^3(y^2-1)=y^3(x^2-1)$
$xy \ne 0 \ \ だから \quad \dfrac{x^2-1}{x^3}=\dfrac{y^2-1}{y^3}$
$y^3z^2-y^3=y^2z^3-z^3 \ \ より \quad y^3(z^2-1)=z^3(y^2-1)$
$yz \ne 0 \ \ だから \quad \dfrac{y^2-1}{y^3}=\dfrac{z^2-1}{z^3}$
$\therefore \ \ \dfrac{x^2-1}{x^3}=\dfrac{y^2-1}{y^3}=\dfrac{z^2-1}{z^3}$
$したがって(1)の関数f(t) を用いると \quad f(x)=f(y)=f(z)\ \ (x < y < z)\ \ とおける。$
$すなわち \ \ x,\ y,\ z\ の条件は \ y=f(t)\ \ のグラフと直線 \ y=k\ \ (k\ は定数)\ が共有点を$
$3\ 個もつことである。$
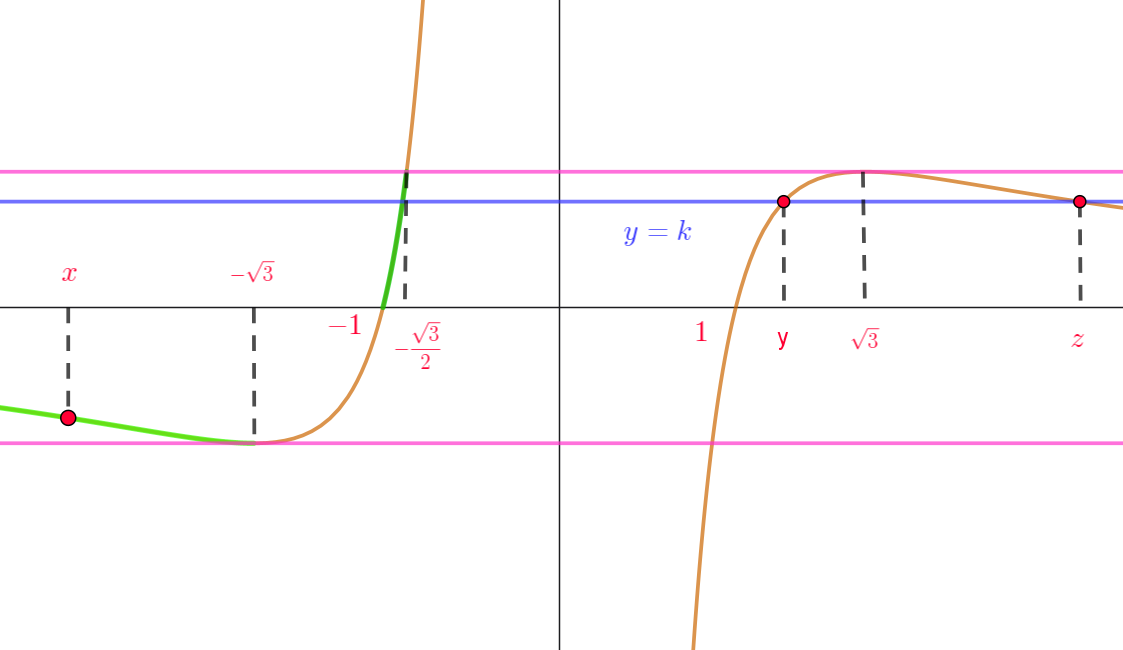
$f(t)\ が極大値をとるときの直線 \ k=\dfrac{2\sqrt{3}}{9}\ と$
$y=f(t)\ との他の共有点の \ t\ 座標は$
$\dfrac{t^2-1}{t^3}=\dfrac{2\sqrt{3}}{9}\ \ より$
$2\sqrt{3}t^3-9t^2+9=0$
$t=\sqrt{3}\ \ を重解にもつことに注意して因数分解すると$
$(t-\sqrt{3})^2(2\sqrt{3}t+3)=0$
$よって \quad t=-\dfrac{3}{2\sqrt{3}}=-\dfrac{\sqrt{3}}{2}$
$共有点を\ 3\ 個もつのは \quad -\dfrac{2\sqrt{3}}{9} < k < \dfrac{2\sqrt{3}}{9} \ \ のときであるが、$
$このとき、 x\ が取り得る値の範囲は \quad x < -\sqrt{3},\quad -1 < x < -\dfrac{\sqrt{3}}{2}$
メインメニュー に戻る