東京科学(理系) 2025年 問題2
$空間の点(0,\ 0,\ 1)\ を通り \ (1,\ -1,\ 0)\ を方向ベクトルとする直線を \ \ell \ \ とし、点(1,\ 0,\ 3)\ を通り \ (0,\ 1,\ -2)\ を$
$方向ベクトルとする直線を \ m \ とする。$
$(1)\ \ P\ を \ \ell \ 上の点とし、Q\ を \ m\ 上の点とする。また、直線PQ\ は直線 \ \ell \ と直線 \ m\ に垂直であるとする。$
$\quad このとき \ P\ と \ Q\ の座標、および線分PQ\ の長さを求めよ。$
$(2)\ \ \ell \ 上に \ 2\ 点 \ A=(t,\ -t,\ 1),\ \ B=(2+t+\sin t,\ -2-t-\sin t,\ 1)\ \ があり、m \ 上に \ 2\ 点 \ C=(1,\ t,\ 3-2t),$
$\quad D=(1,\ 2+t+\cos t,\ -1-2t-2\cos t) \ があるとする。ただし、t\ は実数とする。四面体 \ ABCD\ の体積を$
$\quad V(t)\ とする。V(0)\ を求めよ。$
$(3)\ \ t\ が \ \ t \geqq 0 \ \ を動くとき、V(t)\ の最大値と最小値を求めよ。$
(1)
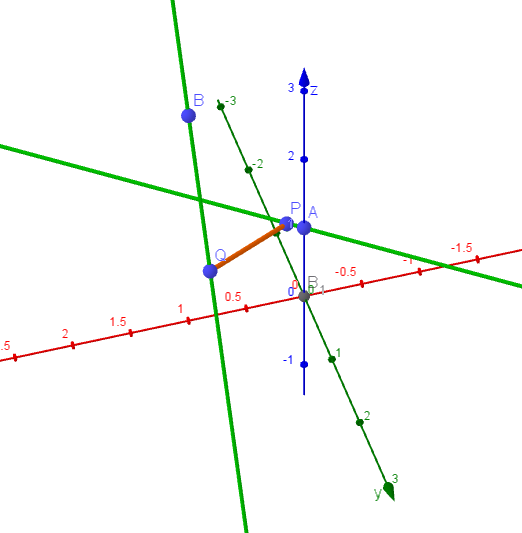
$\vec{OP}=\vec{OA}+t\vec{d}=(0,\ 0,\ 1)+t(1,\ -1,\ 0)=(t,\ -t,\ 1)$
$直線 m \ 上の点を \ B(1,\ 0,\ 3)\ ,\ 方向ベクトルを \ \ \vec{d'}=(0,\ 1,\ -2)\ とすると$
$\vec{OQ}=\vec{OB}+u\vec{d'}=(1,\ 0,\ 3)+u(0,\ 1,\ -2)=(1,\ u,\ 3-2u)$
$よって \quad \vec{PQ}=\vec{OQ}-\vec{OP}=(1-t,\ u+t,\ 2-2u)$
(i)$\ \ PQ \perp \ell \ \ より \quad \vec{PQ} \cdot \vec{d}=0$
$\quad (1-t,\ u+t,\ 2-2u) \cdot (1,\ -1,\ 0)=0 \qquad (1-t)-(u+t)=0$
$\quad 1-2t-u=0 \hspace{5em}①$
(ii)$\ \ PQ \perp m \ \ より \quad \vec{PQ} \cdot \vec{d'}=0$
$\quad (1-t,\ u+t,\ 2-2u) \cdot (0,\ 1,\ -2)=0 \qquad (u+t)-2(2-2u)=0$
$\quad -4+t+5u=0 \hspace{5em}②$
$①+② \times 2 \ \ より \quad -7+9u=0 \qquad u=\dfrac{7}{9}$
$①に代入して \quad 2t=1-u=1-\dfrac{7}{9}=\dfrac{2}{9} \qquad t=\dfrac{1}{9}$
$よって \quad \vec{OP}=(\dfrac{1}{9},\ -\dfrac{1}{9},\ 1),\qquad \vec{OQ}=(1,\ \dfrac{7}{9},\ \dfrac{13}{9})$
$\vec{PQ}=(\dfrac{8}{9},\ \dfrac{8}{9},\ \dfrac{4}{9})$
$|\vec{PQ}|=\dfrac{4}{9}|(2,\ 2,\ 1)|=\dfrac{4}{9} \times \sqrt{2^2+2^2+1^2}=\dfrac{4}{3}$
$以上より \quad P(\dfrac{1}{9},\ -\dfrac{1}{9},\ 1),\quad Q=(1,\ \dfrac{7}{9},\ \dfrac{13}{9}),\quad 線分PQ\ の長さ=\dfrac{4}{3}$
(2)
$V(0)\ は(3)で \ V(t)\ を求めて \ t=0 \ とおけばよいが、あえて \ V(0)\ を先に求めさせるということだから、$
$V(0) \ と \ V(t)\ をそれぞれ別の方法で求めることにする。$
$t=0 \ のとき \quad A=(0,\ 0,\ 1),\ \ B=(2,\ -2,\ 1),\ \ C=(1,\ 0,\ 3),\ \ D=(1,\ 3,\ -3)$
(i)$\ \ \triangle ABC \ \ の面積を求める$
$\quad AB^2=(2-0)^2+(-2-0)^2+(1-1)^2=8$
$\quad AC^2=(1-0)^2+(0-0)^2+(3-1)^2=5$
$\quad BC^2=(1-2)^2+(0+2)^2+(3-1)^2=9$
$\quad \triangle ABC \ \ に余弦定理を用いて$
$\quad \cos A=\dfrac{AB^2+AC^2-BC^2}{2AB \cdot AC}=\dfrac{8+5-9}{2 \times \sqrt{8} \times \sqrt {5}}=\dfrac{1}{\sqrt{10}}$
$\quad \sin A=\sqrt{1-\dfrac{1}{10}}=\dfrac{3}{\sqrt{10}}$
$\quad \triangle ABC=\dfrac{1}{2} \times AB \times AC \times \sin A=\dfrac{1}{2} \times \sqrt{8} \times \sqrt{5} \times \dfrac{3}{\sqrt{10}}=3$
(ii)$\ \ 点D\ から \ \triangle ABC \ に下ろした垂線の長さを求める$
$\quad 3\ 点 \ A,\ B,\ C\ を通る平面を \ \alpha : ax+by+cz=d \ \ とおくと$
$\quad A=(0,\ 0,\ 1)\ \ を通るから \quad c=d \hspace{11em}①$
$\quad B=(2,\ -2,\ 1)\ \ を通るから \quad 2a-2b+c=d \hspace{5.3em}②$
$\quad C=(1,\ 0,\ 3) \ \ を通るから \quad a+3c=d \hspace{9em}③$
$\quad ①を③に代入して \quad a=-2d $
$\quad これらを②に代入して \quad -4d-2b+d=d \qquad b=-2d$
$\quad よって \quad \alpha : -2dx-2dy+dz=d \quad すなわち \quad 2x+2y-z=-1$
$\quad \alpha \ の法線ベクトルは \quad \vec{n}=(2,\ 2,\ -1)$
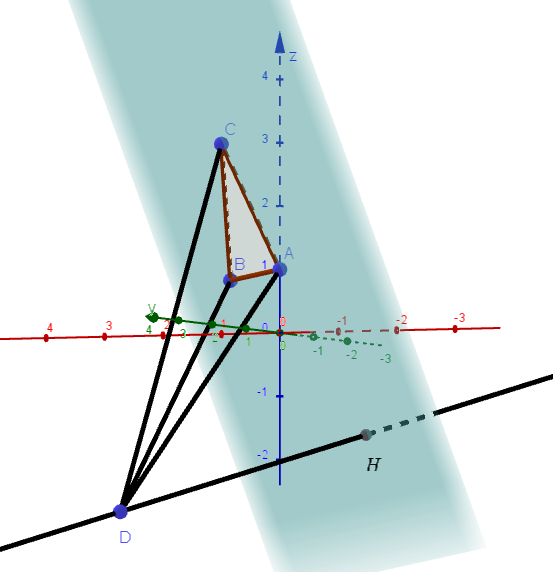
$\vec{DH} /\!/ \vec{n} \ \ だから \quad \vec{DH}=k\vec{n}\ \ (k\ は実数) \ \ とおける$
$\vec{OH}-\vec{OD}=k\vec{n}$
\begin{eqnarray*} \vec{OH} &=&\vec{OD}+k\vec{n}\\ \\ &=&(1,\ 3,\ -3)+k(2,\ 2,\ -1)\\ \\ &=&(1+2k,\ 3+2k,\ -3-k) \end{eqnarray*}
$点H\ は平面 \alpha \ 上の点だから \quad 2(1+2k)+2(3+2k)-(-3-k)=-1$
$9k=-12 \qquad \therefore \ \ k=-\dfrac{4}{3}$
$よって \quad \vec{DH}=-\dfrac{4}{3}\vec{n} \ \ だから \quad DH=\dfrac{4}{3}\sqrt{2^2+2^2+(-1)^2}=4$
(i),(ii)$\ \ より$
$V(0)=\dfrac{1}{3} \times \triangle ABC \times DH=\dfrac{1}{3} \times 3 \times 4=4$
(3)
$A=(t,\ -t,\ 1),\quad B=(2+t+\sin t,\ -2-t-\sin t,\ 1)$
$C=(1,\ t,\ 3-2t),\quad D=(1,\ 2+t+\cos t,\ -1-2t-2\cos t) \ \ より$
$\vec{AB}=\vec{OB}-\vec{OA}=(2+t+\sin t,\ -2-t-\sin t,\ 1)-(t,\ -t,\ 1)=(2+\sin t,\ -2-\sin t,\ 0)$
$\vec{AC}=\vec{OC}-\vec{OA}=(1,\ t,\ 3-2t)-(t,\ -t,\ 1)=(1-t,\ 2t,\ 2-2t)$
$\vec{AD}=\vec{OD}-\vec{OA}=(1,\ 2+t+\cos t,\ -1-2t-2\cos t)-(t,\ -t,\ 1)=(1-t,\ 2+2t+\cos t,\ -2-2t-2\cos t)$
$\triangle ABC=S \ \ とおくと$
\begin{eqnarray*} S &=&\dfrac{1}{2}AB \times AC \times \sin A\\ \\ &=&\dfrac{1}{2}AB \times AC \times \sqrt{1-\cos ^2 A}\\ \\ &=&\dfrac{1}{2}|\vec{AB}||\vec{AC}|\sqrt{1-\Big(\dfrac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}||\vec{AC}|}\Big)^2}\\ \\ &=&\dfrac{1}{2}|\sqrt{|\vec{AB}|^2|\vec{AC}|^2-(\vec{AB} \cdot \vec{AC}) ^2}\\ \\ &=&\dfrac{1}{2}|\sqrt{\{(2+\sin t)^2+(-2-2\sin t)^2\}\{(1-t)^2+(2t)^2+(2-2t)^2\}-\{(2+\sin t)(1-t)+(-2-\sin t)(2t)) ^2\}^2}\\ \\ &=&\dfrac{1}{2}|\sqrt{2(2+\sin t)^2 \times (9t^2-10t+5) -(2+\sin t)^2(1-3t)^2}\\ \\ &=&\dfrac{1}{2}(2+\sin t)\sqrt{2(9t^2-10t+5) -(1-3t)^2}\\ \\ &=&\dfrac{1}{2}(2+\sin t)\sqrt{9t^2-14t+9}\\ \end{eqnarray*}
$\triangle ABC \ の作る平面に垂直で、始点A,\ \ 大きさ \ S\ のベクトルを \ \ \vec{AP}=(p_1,\ p_2,\ p_3)\ \ とおくと$
$p_1^2+p_2^2+p_3^2=S^2 \hspace{18em}①$
$\vec{p} \perp \vec{AB} \ \ より \quad (2+\sin t)p_1+(-2-\sin t)p_2=0 \hspace{5em}②$
$\vec{p} \perp \vec{AC} \ \ より \quad (1-t)p_1+ 2tp_2+(2-2t)p_3=0 \hspace{5em}③$
$②より \quad (2+\sin t)(p_1-p_2)=0 \qquad 2+\sin t > 0 \ \ だから \quad p_2=p_1$
$これを③に代入して \quad (1+t)p_1=(2t-2)p_3$
$t \ne 1 \ のとき \quad p_3=\dfrac{t+1}{2t-2}p_1$
$p_2,\ p_3\ を①に代入して$
$p_1^2+p_1^2+\big(\dfrac{t+1}{2t-2}\big)^2p_1^2=S^2$
$\big(2+\dfrac{(t+1)^2}{4(t-1)^2}\big)p_1^2=S^2$
$\dfrac{8(t-1)^2+(t+1)^2}{4(t-1)^2}p_1^2=S^2$
$p_1^2=\dfrac{4(t-1)^2}{9t^2-14t+9}S^2$
$p_1=\pm \dfrac{2(t-1)}{\sqrt{9t^2-14t+9}}S$
$p_3=\dfrac{t+1}{2t-2}p_1=\dfrac{t+1}{2t-2} \times \big(\pm \dfrac{2(t-1)}{\sqrt{9t^2-14t+9}}\big)S=\pm \dfrac{t+1}{\sqrt{9t^2-14t+9}}S$
$なお、t=1 \ \ のときは \ \ p_1=p_2=0 ,\ \ p_3=\pm S =\pm (2+\sin 1)\ \ となるが上式に \ t=1 \ を代入した値に一致する。$
$S=\dfrac{1}{2}(2+\sin t)\sqrt{9t^2-14t+9} \quad だから$
$p_1=p_2=\pm \dfrac{2(t-1)}{\sqrt{9t^2-14t+9}} \times \dfrac{1}{2}(2+\sin t)\sqrt{9t^2-14t+9}=\pm (t-1)(2+\sin t)$
$p_3=\pm \dfrac{t+1}{\sqrt{9t^2-14t+9}} \times \big(\pm \dfrac{1}{2}(2+\sin t)\sqrt{9t^2-14t+9}\big)=\pm \dfrac{1}{2}(t+1)(2+\sin t)$
$\vec{AP}=\pm ((t-1)(2+\sin t),\ (t-1)(2+\sin t),\ \dfrac{1}{2}(t+1)(2+\sin t))=\pm (2+\sin t)(t-1,\ t-1,\ \dfrac{t+1}{2})$
$\dfrac{\vec{p}}{|\vec{p}|}=\vec{e} \ \ とおくと \quad |\vec{p}|=S \ \ だから \quad \vec{p}=S\vec{e}$
$点D\ から平面ABC \ に下ろした垂線の長さ \ h\ は \quad h=|\vec{AD} \cdot \vec{e}| \ \ だから$
\begin{eqnarray*} V &=&\dfrac{1}{3}Sh\\ \\ &=&\dfrac{1}{3} S|\vec{AD}\cdot \vec{e}|\\ \\ &=&\dfrac{1}{3}|\vec{AD}\cdot S\vec{e}|\\ \\ &=&\dfrac{1}{3}|\vec{AD}\cdot \vec{p}|\\ \\ &=&\dfrac{1}{3}\big|(2+\sin t)\big\{(1-t)((t-1)+(2+2t+\cos t)(t-1)+(-2-2t-2\cos t)(\dfrac{t+1}{2})\}\big|\\ \\ &=&\dfrac{1}{3}(2+\sin t)\big|-(t-1)^2+(2+2t+\cos t)(t-1)-(1+t+\cos t)(t+1)\big|\\ \\ &=&\dfrac{1}{3}(2+\sin t)\big|-4-2\cos t\big|\\ \\ &=&\dfrac{2}{3}(2+\sin t)(2+\cos t)\\ \end{eqnarray*}
$V\ は周期 \ 2\pi \ の周期関数だから \ [0,\ 2\pi]\ \ で考えればよい。$
\begin{eqnarray*} V' &=&\dfrac{2}{3}(\cos t(2+\cos t)-\sin t(2+\sin t))\\ \\ &=&\dfrac{2}{3}(2(\cos t-\sin t)+\cos ^2t-\sin ^2t)\\ \\ &=&\dfrac{2}{3}(\cos t-\sin t)(2+\cos t+\sin t)\\ \end{eqnarray*} $2+\cos t+\sin t > 0 \ \ だから \ \ V'=0\ \ より \quad \cos t- \sin t=0 \qquad \tan t=1 \qquad t=\dfrac{\pi}{4},\quad \dfrac{5}{4}\pi$
$増減表$
\[ \begin{array}{c||c|c|c|c|c} t & 0 & \cdots & \dfrac{\pi}{4} & \cdots & \dfrac{5\pi}{4} &\cdots & 2\pi \\ \hline V'& & + & 0 & - & 0 & + &\\ \hline v& & \nearrow & 極大 & \searrow & 極小 & \nearrow & \\ \end{array} \]
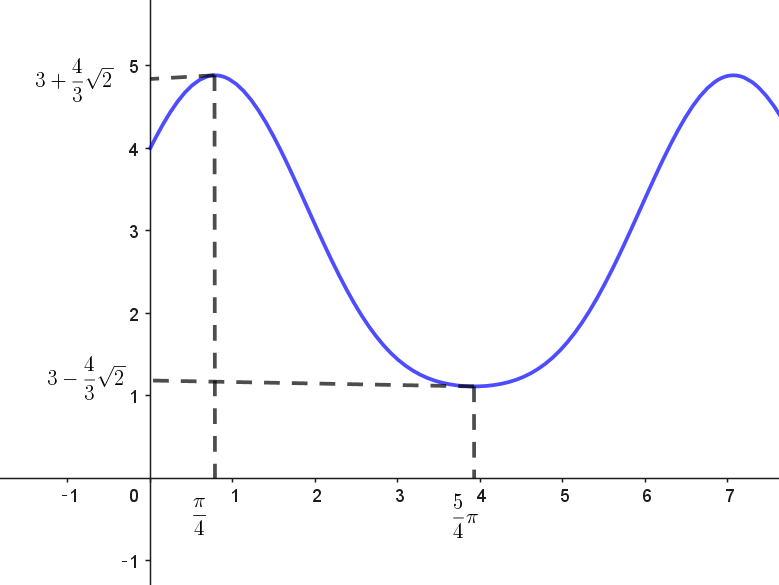
$t=\cfrac{\pi}{4}+2k\pi\ で\ V\ は極大かつ最大となり、最大値は$
$V(\dfrac{\pi}{4})=\dfrac{2}{3}(2+\sin \dfrac{\pi}{4})(2+\cos \dfrac{\pi}{4})=\dfrac{2}{3}(2+\dfrac{\sqrt{2}}{2})(2+\dfrac{\sqrt{2}}{2})=3+\dfrac{4}{3}\sqrt{2}$
$t=\cfrac{5}{4}\pi+2k\pi \ でVは極小かつ最小となり、最小値は$
$V(\dfrac{5}{4}\pi)=\dfrac{2}{3}(2+\sin \dfrac{5}{4}\pi)(2+\cos \dfrac{5}{4}\pi)=\dfrac{2}{3}(2-\dfrac{\sqrt{2}}{2})(2-\dfrac{\sqrt{2}}{2})=3-\dfrac{4}{3}\sqrt{2}$
メインメニュー に戻る