東北大学(理系) 2025年　問題5


$S\ を \ xyz\ 空間内の原点O(0,\ 0,\ 0)\ を中心とする半径 \ 1\ の球面とする。また、点P(a,\ b,\ c)\ を点N(0,\ 0,\ 1)\ とは$
$異なる球面 \ S\ 上の点とする。点P\ と点N\ を通る直線 \ \ell \ と \ xy\ 平面との交点を \ Q\ とおく。このとき、以下の問$
$いに答えよ。$
$(1)\ \ 点Q\ の座標を \ a、\ b、\ c\ を用いて表せ。$
$(2)\ \ xy\ 平面上の点(p,\ q,\ 0)\ と点N\ を通る直線を \ m\ とする。直線 \ m\ と球面 \ S\ の交点のうち、点 \ N\ 以外の交点$
$\quad の座標を \ p,\ q\ を用いて表せ。$
$(3) \ \ 点(0,\ 0,\ \dfrac{1}{2})\ を通り、ベクトル(3,\ 4,\ 5)\ に直交する平面 \ \alpha \ を考える。点 \ P\ が平面 \ \alpha \ と球面 \ S\ との交わりを$
$\quad を動くとき、点 \ Q\ は \ xy\ 平面上の円周上を動くことを示せ。$


(1)

　

$\vec{NP}=(a,\ b,\ c)-(0,\ 0,\ 1)=(a,\ b,\ c-1)$

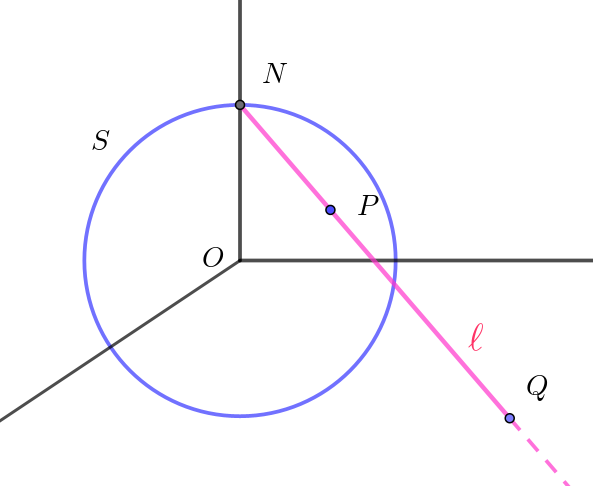
$\vec{OQ}=\vec{ON}+t\vec{NP} \ \ (t\ は実数)\ \ とおけるから$

$\vec{OQ}=(0,\ 0,\ 1)+t(a,\ b,\ c-1)=(ta,\ tb,\ 1+t(c-1))$

$点Q\ は\ xy\ 平面上にあるから \quad 1+t(c-1)=0$

$点P(a,\ b,\ c)\ は点N(0,\ 0,\ 1)\ とは異なる点だから \ \ c \ne 1$

$よって \quad t=\dfrac{1}{1-c}$

$\therefore \ \ \vec{OQ}=(\dfrac{a}{1-c},\ \dfrac{b}{1-c},\ 0)\ \ より \quad Q=(\dfrac{a}{1-c},\ \dfrac{b}{1-c},\ 0)$


(2)

　

$xy\ 平面上の点(p,\ q,\ 0)\ をQ とすると$

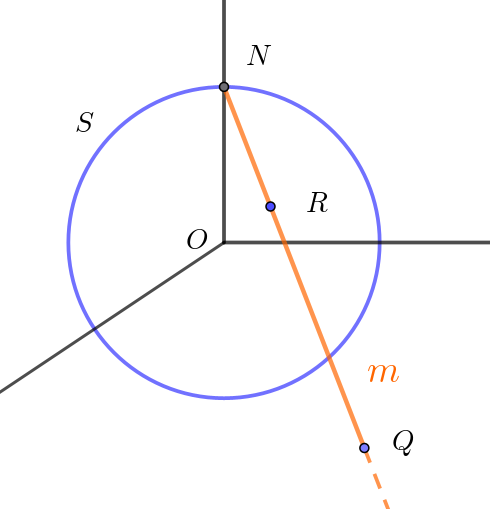
$\vec{NQ}=(p,\ q,\ 0)-(0,\ 0,\ 1)=(p,\ q,\ -1)$

$直線 \ m\ と球面 \ S\ の交点のうち、点 \ N\ 以外の交点を \ R\ とおくと$

$\vec{OR}=\vec{ON}+s\vec{NQ}\ \ (s\ は実数)\ \ とおけるから$

$\vec{OR}=(0,\ 0,\ 1)+s(p,\ q,\ -1)=(sp,\ sq,\ 1-s))$

$点Rは\ 球面 \ S: x^2+y^2+z^2=1 \ \ 上の点だから $

$s^2p^2+s^2q^2+(1-s)^2=1$

$(1+p^2+q^2)s^2=2s$

$点R\ は点N(0,\ 0,\ 1)\ とは異なる点だから \ \ s \ne 0$

$よって \quad s=\dfrac{2}{1+p^2+q^2}$

$1-s=1- \dfrac{2}{1+p^2+q^2}=-\dfrac{1-p^2-q^2}{1+p^2+q^2}$

$\therefore \ \ \vec{OR}=(\dfrac{2p}{1+p^2+q^2},\ \dfrac{2q}{1+p^2+q^2},\ -\dfrac{1-p^2-q^2}{1+p^2+q^2}\big)\ \ より$

$R(\dfrac{2p}{1+p^2+q^2},\ \dfrac{2q}{1+p^2+q^2},\ -\dfrac{1-p^2-q^2}{1+p^2+q^2})$


(3)

　

$平面 \ \alpha \ はベクトル(3,\ 4,\ 5)\ に直交するから、法線ベクトルが$

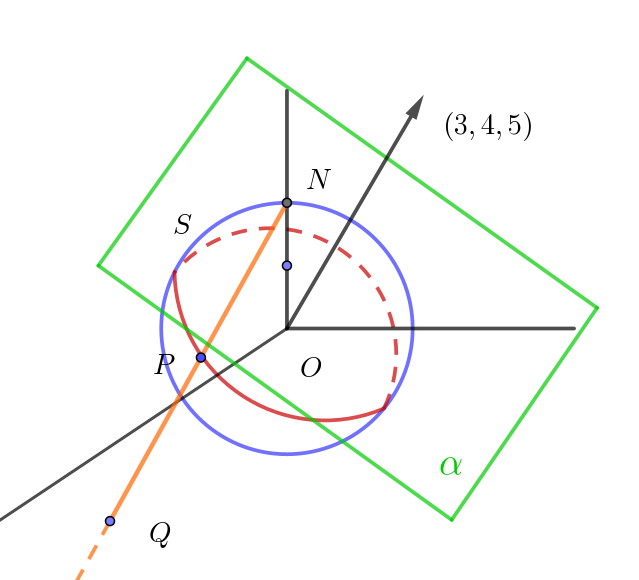
$(3,\ 4,\ 5)\ \ であり、点(0,\ 0,\ \dfrac{1}{2})\ を通るから$

$3x+4y+5(z-\dfrac{1}{2})=0 \quad とおける$

$\therefore \ \ \alpha : 3x+4y+5z=\dfrac{5}{2}$

$点P(a,\ b,\ c)\ \ は平面 \ \alpha \ 上にあるから \quad 3a+4b+5c=\dfrac{5}{2} \hspace{4em}①$

$点P(a,\ b,\ c)\ \ は球面 \ S\ 上の点だから \quad a^2+b^2+c^2=1 \hspace{5em}②$

$(1)より \quad Q(\dfrac{a}{1-c},\ \dfrac{b}{1-c},\ 0)$

$点Q\ の軌跡を求めればよいから \quad x=\dfrac{a}{1-c},\quad y=\dfrac{b}{1-c}\quad とおくと$

$a=(1-c)x,\quad b=(1-c)y \hspace{5em}③$

$③を①に代入して$

$3(1-c)x+4(1-c)y+5c=\dfrac{5}{2}$

$(5-3x-4y)c=\dfrac{5}{2}-3x-4y$

$ここで、Q(x,\ y)\ において \ \ 5-3x-4y=0\ \ とすると$

$5-\dfrac{3a}{1-c}-\dfrac{4b}{1-c}=0$

$3a+4b+5c=5 \ \ となって①に矛盾する。よって \quad 5-3x-4y \ne 0$

$c=\dfrac{\dfrac{5}{2}-3x-4y}{5-3x-4y}=\dfrac{5-2(3x+4y)}{2(5-3x-4y)}$

$1-c=1-\dfrac{5-2(3x+4y)}{2(5-3x-4y)}=\dfrac{5}{2(5-2x-4y)}$

$これを③に代入して$

$a=\dfrac{5x}{2(5-2x-4y)},\quad b=\dfrac{5y}{2(5-2x-4y)}$

$これらを②に代入して$

$\big(\dfrac{5x}{2(5-2x-4y)}\big)^2+\big(\dfrac{5y}{2(5-2x-4y)}\big)^2+\big(\dfrac{5-2(3x+4y)}{2(5-3x-4y)}\big)^2=1$

$25x^2+25y^2+25 -20(3x+4y)+4(3x+4y)^2=4\big(25-10(3x+4y)+(3x+4y)^2\big)$

$25x^2+25y^2+20(3x+4y)-75=0$

$x^2+y^2+\dfrac{4}{5}(3x+4y)-3=0$

$\big(x+\dfrac{6}{5}\big)^2+\big(y+\dfrac{8}{5}\big)^2=7$

$よって \quad 点 \ Q\ は \ xy\ 平面上で、中心(-\dfrac{6}{5},\ -\dfrac{8}{5}),\ \ 半径 \ \sqrt{7} \ \ の円周上を動く。$


ページの先頭へ↑



メインメニュー　に戻る