東北大学(理系) 2025年　問題4


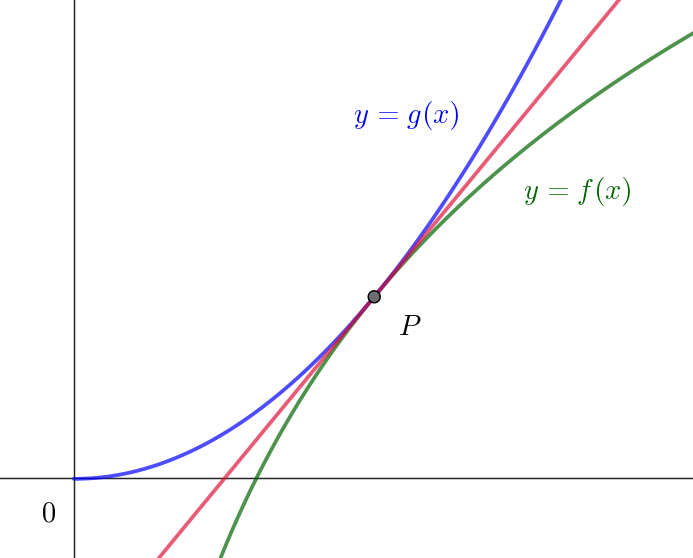
$n\ を正の整数、a\ を正の実数とし、関数 \ f(x)\ と \ g(x)\ を次のように定める。$
$\qquad f(x)=n\log x , \quad g(x)=ax^n$
$また、曲線 \ y=f(x)\ と曲線 \ y=g(x)\ が共有点をもち、その共有点における \ 2\ つの曲線の接線が一致している$
$とする。このとき、以下の問いに答えよ。$
$(1)\ \ a\ の値を求めよ。$
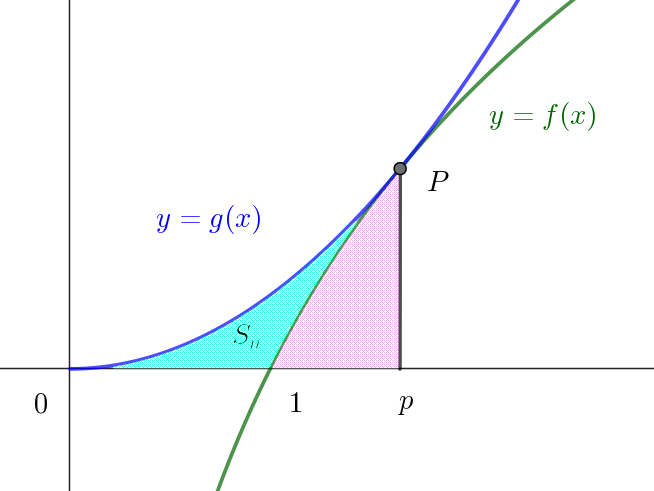
$(2)\ \ この \ 2\ つの曲線と \ x\ 軸で囲まれた部分の面積 \ S_n \ を求めよ。$
\[(3) \ \ (2)で求めた \ S_n \ に対し、極限 \ \ \lim_{n \rightarrow \infty} S_n \ \ を求めよ。\]


(1)

　

$共有点をP(p,\ q)\ \ とおくと$

$\quad n\log p=ap^n \hspace{5em}①$

$f'(x)=\dfrac{n}{x},\quad g'(x)=nax^{n-1}$

$共有点P(p,\ q)\ における \ 2\ つの接線の傾きは等しいから$

$\quad \dfrac{n}{p}=nap^{n-1}$

$両辺に \ \dfrac{p}{n}\ をかけて$

$\quad 1=ap^n \hspace{5em}②$

$②を①に代入して \quad n\log p=1$

$\log p=\dfrac{1}{n} \qquad \therefore \ \ p=e^{\scriptsize{\dfrac{1}{n}}}$

$②に代入して \quad a=p^{-n}=\big(e^{\scriptsize{\dfrac{1}{n}}}\big)^{-n}=e^{-1}=\dfrac{1}{e}$


(2)

　

\begin{eqnarray*} S_n &=&\int_0^pg(x)dx -\int_1^pf(x)dx\\ \\ &=&\int_0^p \dfrac{1}{e}x^ndx -\int_1^p n\log xdx\\ \\ &=&\dfrac{1}{e(n+1)}\big[x^{n+1}\big]_0^p -n\Big\{\big[x\log x \big]_1^p - \int _1^p dx\Big\}\\ \\ &=&\dfrac{p^{n+1}}{e(n+1)} -n\big\{p\log p -(p-1)\big\}\\ \\ &=&\dfrac{e^{\scriptsize{\dfrac{n+1}{n}}}}{e(n+1)} -n\big(e^{\scriptsize{\dfrac{1}{n}}} \times \dfrac{1}{n} - e^{\scriptsize{\dfrac{1}{n}}}+1\big)\\ \\ &=&\dfrac{e^{\scriptsize{1+\dfrac{1}{n}}}}{e(n+1)} -e^{\scriptsize{\dfrac{1}{n}}} +n\big(e^{\scriptsize{\dfrac{1}{n}}}-1\big)\\ \\ &=&\dfrac{e^{\scriptsize{\dfrac{1}{n}}}}{n+1} -e^{\scriptsize{\dfrac{1}{n}}} +n\big(e^{\scriptsize{\dfrac{1}{n}}}-1\big)\\ \\ &=&-(1-\dfrac{1}{n+1})e^{\scriptsize{\dfrac{1}{n}}} +n\big(e^{\scriptsize{\dfrac{1}{n}}}-1\big)\\ \\ &=&-\dfrac{n}{n+1}e^{\scriptsize{\dfrac{1}{n}}} +n\big(e^{\scriptsize{\dfrac{1}{n}}}-1\big)\\ \end{eqnarray*}

(3)


$(2)の \ S_n\ で \ \ n \longrightarrow \infty \ \ のとき、$

$第 \ 1\ 項 \ \ \longrightarrow -1 \times e^0=-1 $

$第 \ 2\ 項については \quad \dfrac{1}{n}=x \ \ とおくと \quad n\big(e^{\scriptsize{\dfrac{1}{n}}}-1\big)=\dfrac{e^x -1}{x}\\$
\[ところで、x\ が実数のとき \quad \lim_{x \rightarrow 0} (1+x)^{\scriptsize{\dfrac{1}{x}}}=e \quad だから \ \ (これは証明なしでつかってよいでしょう)\] \[\lim_{x \rightarrow 0} \dfrac{\log(1+x)}{x}=\lim_{x \rightarrow 0} \log (1+x)^{\scriptsize{\dfrac{1}{x}}}=\log e=1\] $e^x-1=t \ \ とおくと \quad x=\log(1+t)\ \ で \quad x \longrightarrow 0 \ \ のとき \quad t \longrightarrow 0 \quad だから$

\[\lim_{x \rightarrow 0} \dfrac{e^x -1}{x}=\lim_{t \rightarrow 0} \dfrac{t}{\log(1+t)}=1\] $よって \quad 第2項 \ \ \longrightarrow 1$

\[ゆえに \quad \lim_{n \rightarrow \infty} S_n =-1+1=0\]

ページの先頭へ↑



メインメニュー　に戻る