東北大学(理系) 2025年 問題3
$a\ を実数とし、関数 \ f(x)\ を次のように定める。$
$\quad f(x)=x^4+\dfrac{4a}{3}x^3+(a+2)x^2$
$このとき、以下の問いに答えよ。$
$(1)\ \ 関数 \ f(x)\ が極大値をもつような \ a\ のとり得る値の範囲を求めよ。$
$(2)\ \ 関数 \ f(x)\ が \ x=0\ で極大値をもつような \ a\ のとり得る値の範囲を求めよ。$
(1)
$f(x)=x^4+\dfrac{4a}{3}x^3+(a+2)x^2 \ \ より$
$f'(x)=4x^3+4ax^2+2(a+2)x=2x(2x^2+2ax+a+2)$
$2x^2+2ax+a+2=0 \ \ の解を \ \ \alpha, \ \ \beta \ \ とすると$
$f'(x)=0 \ \ が異なる \ 3\ つの実数解 \ \ (\alpha < \beta)\ \ をもつような \ f'(x) \ のグラフは下図の \ 3\ 通りで$
$\hspace{4em} (ア)\ \ \alpha < \beta < 0 \ \ のとき \hspace{10em} (イ)\ \ \alpha < 0 < \beta \ \ のとき \hspace{8em} (ウ)\ \ 0 < \alpha < \beta \ \ のとき$



$f'(x)\ の符号は、いずれの場合も \ \ 負、0、正、0、負、0 、正\ だから、$
$f'(x)=0 \ \ となる \ x\ で順に \ \ 極小、極大、極小\ となる。$
$したがって \quad f(x)\ が極大値をもつような条件は \ \ f'(x)=0\ が異なる \ 3\ つの実数解をもつことである。$
$よって \quad 2x^2+2ax+a+2=0 \ \ が \ 0\ 以外の異なる実数解をもてばよいからその条件は$
(i)$\ \ \dfrac{D}{4}=a^2-2(a+2) > 0$
$\quad a^2-2a-4 > 0$
$\quad a < 1-\sqrt{5},\quad a > 1+\sqrt{5}$
(ii)$\ \ x \ne 0 \ \ だから \quad a + 2 \ne 0 \qquad \therefore \ \ a \ne -2$
(i),(ii)$\ \ より \quad a < 1-\sqrt{5} \quad (ただし \ \ a \ne -2) , \quad a > 1+\sqrt{5}$
(2)
$f(x)\ が \ x=0\ で極大値をもつのは(1)の図で \quad \alpha < 0 < \beta \quad の場合である。$
$増減表は$
\[ \begin{array}{c||c|c|c|c|c} x& \cdots & \alpha & \cdots & 0 & \cdots & \beta & \cdots \\ \hline f'(x)& - & 0 & + & 0 & - & 0 & +\\ \hline f(x)& \searrow & 極小 & \nearrow & 極大 & \searrow & 極小 & \nearrow \\ \end{array} \]
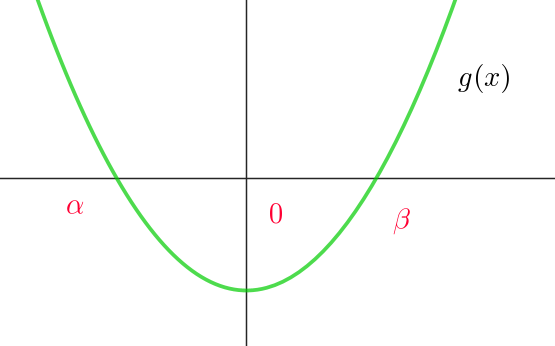
$g(x)=0 \ \ の \ 2\ つの実数解 \ \ \alpha ,\ \beta \ \ が \quad \alpha < 0 < \beta \ \ である必要十分条件は$
$g(0) < 0$
$a+2 < 0$
$\therefore \ \ a < -2$
メインメニュー に戻る