東北大学(理系) 2024年　問題6


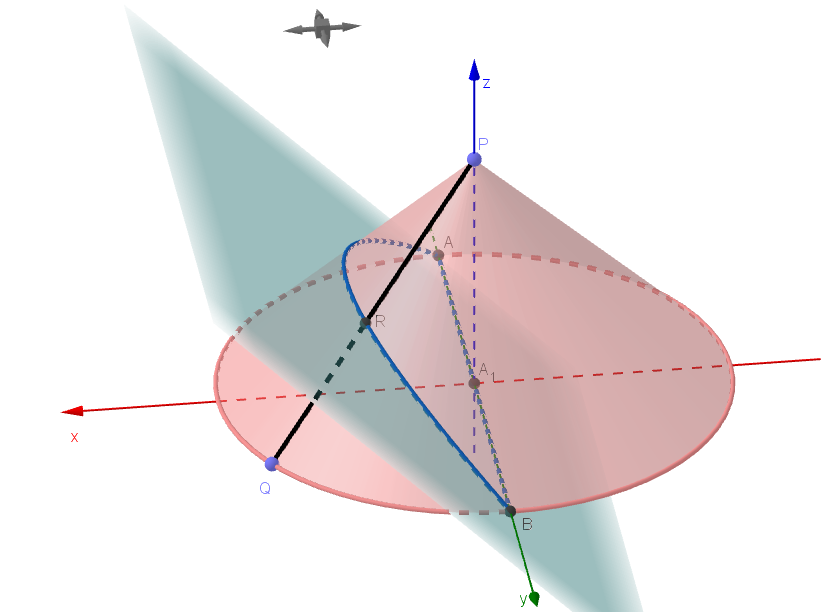
$xyz\ 空間内の \ xy\ 平面上にある円 \ C:x^2+y^2=1\ および円板 \ D:x^2+y^2 \leqq 1 \ を考える。D\ を底面とし$
$点P(0,\ 0,\ 1)\ を頂点とする円錐を \ K\ とする。A(0,\ -1,\ 0),\ B(0,\ 1,\ 0)\ とする。xyz\ 空間内の平面 \ H:z=x $
$を考える。すなわち、H\ は \ xz\ 平面上の直線 \ z=x \ と線分 \ AB\ をともに含む平面である。K\ の側面と \ H\ の$
$交わりとしてできる曲線を \ E\ とする。-\dfrac{\pi}{2} \leqq \theta \leqq \dfrac{\pi}{2} \ を満たす実数 \ \theta \ に対し、円 \ C\ 上の点Q(\cos \theta,\ \sin \theta,\ 0)$
$をとり、線分 \ PQ\ と \ E\ の共有点を \ R\ とする。$
$(1)\ \ 線分 \ PR\ の長さを \ r(\theta)\ とおく。r(\theta)\ を \ \theta \ を用いて表せ。$
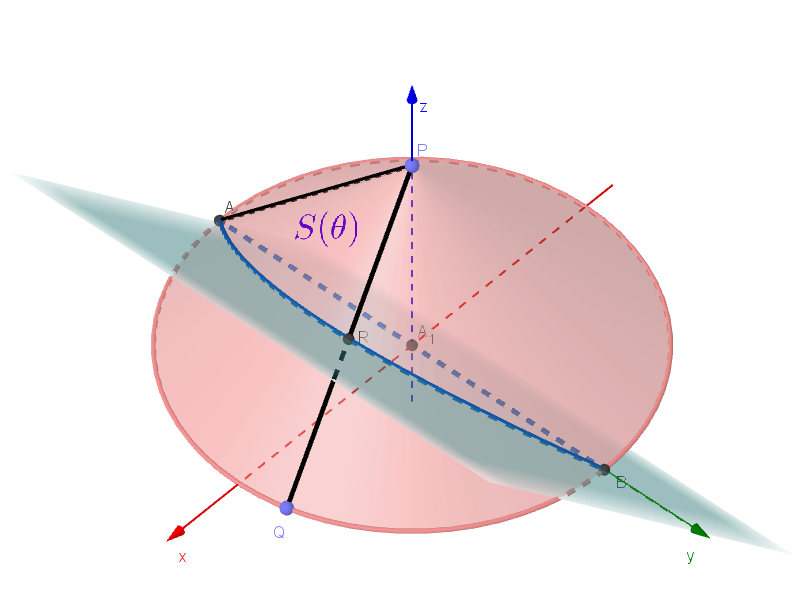
$(2)\ \ 円錐Kの側面のうち、曲線 \ E\ の点 \ A\ から点 \ R\ までを結ぶ部分、線分 \ PA、および線分 \ PR\ により囲まれ$
$\quad た部分の面積を \ S(\theta)\ とおく。\theta \ と実数 \ h\ が条件 \ \ 0 \leqq \theta < \theta + h \leqq \dfrac{\pi}{2} \ \ を満たすとき、次の不等式が成り立つ$
$\quad ことを示せ。$
$\hspace{5em} \cfrac{h\{r(\theta)\}^2}{2\sqrt{2}} \leqq S(\theta +h) -S(\theta) \leqq \cfrac{h\{r(\theta +h)\}^2}{2\sqrt{2}}$
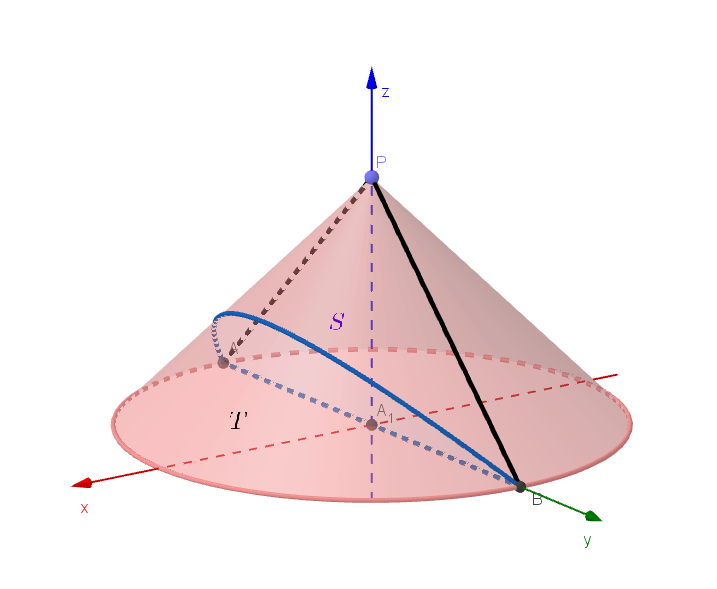
$(3)\ \ 円錐 \ K\ の側面のうち、円 \ C\ の\ x \geqq 0 \ の部分と曲線 \ E\ により囲まれた部分の面積を \ T\ とおく。T\ を求めよ。$
$\quad 必要であれば \ \ \tan \dfrac{\theta}{2} =u \ \ とおく置換積分を用いてもよい。$


(1)

　

$\vec{PQ}=\vec{OQ}-\vec{OP}=(\cos \theta,\ \sin \theta,\ 0)-(0,\ 0,\ 1)=(\cos \theta,\ \sin \theta,\ -1)$

$\vec{PR}=k\vec{PQ}\ \ (k\ は実数)\ \ とおけるから$

$\vec{OR}-\vec{OP}=k\vec{PQ}$

\begin{eqnarray*} \vec{OR} &=&\vec{OP}+k\vec{PQ}\\ \\ &=&(0,\ 0,\ 1)+k(\cos \theta,\ \sin \theta,\ -1)\\ \\ &=&(k\cos \theta,\ k\sin \theta,\ 1-k) \end{eqnarray*}
$点 \ R\ は平面 \ H:z=x \ 上の点だから$

$k\cos \theta =1-k$

$k=\cfrac{1}{1+\cos \theta}$

$\therefore \ \ \vec{OR}=(\cfrac{\cos \theta }{1+\cos \theta},\ \cfrac{\sin \theta}{!+\cos \theta} ,\ \cfrac{\cos \theta }{1+\cos \theta})$

$\{r(\theta)\}^2=|\vec{PR}|^2=k^2|\vec{PQ}|^2=k^2(\cos ^2 \theta+ \sin ^2 \theta + 1)=\cfrac{2}{(1+\cos \theta)^2}$

$\therefore \ \ r(\theta)=\cfrac{\sqrt{2}}{1+\cos \theta}$

　

(2)


$\theta \ は \ xy\ 平面で \ x\ 軸の正方向と \ OR\ のなす角であることに注意して$

$S(\theta)\ の区間 \ (\theta , \ \theta + h) \ の部分を取り出した図が右図である。$

$円 \ C\ 上の点(\cos (\theta+h),\ \sin (\theta +h),\ 0) を \ Q'、線分 \ PQ'\ と \ E\ の$

$共有点を \ R'\ とし、線分 \ PQ\ と \ PQ'\ のなす角を \ \gamma \ とおく。$

$OP=1,\ \ OQ=OQ'=1 ,\ \ OP \perp OQ \ \ だから \ \ PQ=PQ'=\sqrt{2}$

　

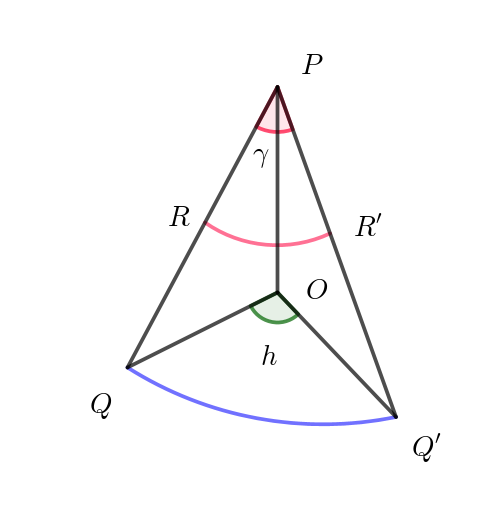
$扇型 \ OQQ' \ において \ \ 弧QQ'=2\pi \times OQ \times \cfrac{h}{2\pi}=h$

$扇型 \ PQQ' \ において \ \ \gamma =2\pi \times \cfrac{弧QQ'}{2\pi \times PQ}=2\pi \times \cfrac{h}{2\pi \sqrt{2}}=\cfrac{h}{\sqrt{2}}$

$r'(\theta)=-\cfrac{\sqrt{2}(-\sin \theta)}{(1+\cos \theta)^2}=\cfrac{\sqrt{2}\sin \theta}{(1+\cos \theta)^2}$

$0 \leqq \theta \leqq \cfrac{\pi}{2} \ \ では \ \ r'(\theta) > 0 \ \ となり \ r(\theta) \ は単調増加である。$

$したがって \quad PR < PR'$

$(中心角 \ \gamma , 半径 \ OR \ の扇型の面積) \leqq S(\theta + h) -S(\theta) \leqq (中心角 \ \gamma , \ 半径 \ OR'\ の扇型の面積)$

$\cfrac{\gamma \{r(\theta)\}^2}{2} \leqq S(\theta +h) -S(\theta) \leqq \cfrac{\gamma \{r(\theta +h)\}^2}{2}$

$よって$

$\cfrac{h\{r(\theta)\}^2}{2\sqrt{2}} \leqq S(\theta +h) -S(\theta) \leqq \cfrac{h\{r(\theta +h)\}^2}{2\sqrt{2}}$


(3)


$(2)より \quad \cfrac{\{r(\theta)\}^2}{2\sqrt{2}} \leqq \cfrac{S(\theta +h) -S(\theta)}{h} \leqq \cfrac{\{r(\theta +h)\}^2}{2\sqrt{2}}$

$h \longrightarrow 0 \quad とすると \quad 右辺 \ \ \longrightarrow \cfrac{\{r(\theta)\}^2}{2\sqrt{2}}$

$また -\cfrac{\pi}{2} \leqq \theta \leqq 0 \ \ では \ \ r'(\theta) < 0 \ \ となり \ \ 　r(\theta) \ は単調減少だから$

$\cfrac{h\{r(\theta + h)\}^2}{2\sqrt{2}} \leqq S(\theta +h) -S(\theta) \leqq \cfrac{h\{r(\theta )\}^2}{2\sqrt{2}}$

$\cfrac{\{r(\theta +h)\}^2}{2\sqrt{2}} \leqq \cfrac{S(\theta +h) -S(\theta)}{h} \leqq \cfrac{\{r(\theta )\}^2}{2\sqrt{2}}$

$h \longrightarrow 0 \quad とすると \quad 左辺 \ \ 　\longrightarrow \cfrac{\{r(\theta)\}^2}{2\sqrt{2}} $

$したがって \quad -\cfrac{\pi}{2} \leqq \theta \leqq \cfrac{\pi}{2} \quad において はさみうちの原理により$

\begin{eqnarray*} S'(\theta) &=&\lim_{h \rightarrow 0}\cfrac{S(\theta +h)-S(\theta)}{h}\\ \\ &=&\cfrac{\{r(\theta)\}^2}{2\sqrt{2}}\\ \\ &=&\cfrac{2}{2\sqrt{2}(1+\cos \theta)^2}\\ \\ &=&\cfrac{1}{\sqrt{2}(1+2\cos ^2 \dfrac{\theta}{2}-1)^2}\\ \\ &=&\cfrac{1}{4\sqrt{2}\cos ^4 \dfrac{\theta}{2}}\\ \end{eqnarray*}
$円錐 \ K\ の側面のうち、曲線 \ E\ の点 \ A\ から点 \ R\ までを結ぶ部分、線分 \ PA、および線分 \ PB\ により囲まれ$

$部分の面積 \ S は$

\[S=\int_{-\scriptsize{\dfrac{\pi}{2}}}^{\scriptsize{\dfrac{\pi}{2}}}\cfrac{d\theta}{4\sqrt{2}\cos ^4 \dfrac{\theta}{2}}= \int_0^{\scriptsize{\dfrac{\pi}{2}}}\cfrac{d\theta}{2\sqrt{2}\cos ^4 \dfrac{\theta}{2}}= \cfrac{1}{\sqrt{2}} \int_0^{\scriptsize{\dfrac{\pi}{2}}}\cfrac{d\theta}{2\cos ^2 \dfrac{\theta}{2} \times \cos ^2 \dfrac{\theta}{2}} \] \[ \tan \dfrac{\theta}{2}=u \ \ とおくと \quad \cfrac{d\theta}{2\cos ^2 \dfrac{\theta}{2}}=du \qquad 1+ \tan^2 \dfrac{\theta}{2}=\cfrac{1}{\cos^2 \dfrac{\theta}{2}} \qquad \begin{array}{c|c} \theta & 0\ \ \rightarrow \dfrac{\pi}{2}\\ \hline u & \ 0 \rightarrow 1 \\ \end{array} \]

　

\begin{eqnarray*} S &=&\cfrac{1}{\sqrt{2}}\int_0^1 (1+u^2)du\\ \\ &=&\cfrac{1}{\sqrt{2}}\big[u+\dfrac{u^3}{3}\big]_0^1\\ \\ &=&\cfrac{2\sqrt{2}}{3} \end{eqnarray*}
$円錐 \ K\ の側面積=\pi \times \sqrt{2}^2 \times \cfrac{2\pi \times 1}{2\pi \times \sqrt{2}}=\sqrt{2}\pi$

$S+T \ は円錐 \ K\ の側面積の半分であるから$

$S+T=\cfrac{\sqrt{2}}{2}\pi$

$よって \quad T=\cfrac{\sqrt{2}}{2}\pi -S=\cfrac{\sqrt{2}}{2}\pi - \cfrac{2\sqrt{2}}{3}$


$(補充)$

$一般に、直円錐の側面を平面で切断したとき、側面の切り口の曲線を「円錐曲線」といいます。$

$本問のように、円錐の軸と母線のなす角と、軸と平面のなす角が等しいとき、切り口は放物線になります。$

$切り方によって他に、楕円(円を含む)、双曲線がありますので、円錐曲線は二次曲線そのものです。$


ページの先頭へ↑



メインメニュー　に戻る