東北大学(理系) 2024年 問題5
\[x \geqq 2 \ \ を満たす実数 \ x\ に対し、 f(x)=\cfrac{\log (2x-3)}{x}\ \ とおく。必要ならば、\lim_{t \rightarrow \infty} \dfrac{\log t}{t}=0 \ \ であること\]
$および、自然対数の底 \ e\ が \ \ 2 < e < 3\ \ を満たすことを証明なしで用いてもよい。$
$(1)\ \ f'(x)=\dfrac{g(x)}{x^2(2x-3)} \ \ とおくとき、関数 \ g(x)\ \ (x \geqq 2)\ \ を求めよ。$
$(2)\ \ (1)で求めた関数 \ g(x)\ に対し、g(\alpha)=0 \ \ を満たす \ 2\ 以上の実数 \ \alpha \ がただ \ 1\ つ存在することを示せ。$
\[(3)\ \ 関数 \ f(x) \ \ (x \geqq 2)\ \ の増減と極限 \ \ \lim_{x \rightarrow \infty} f(x) \ \ を調べ、y=f(x)\ \ (x \geqq 2)\ \ のグラフの概形をxy平面上に\]
$\quad 描け。ただし、(2)の\alpha \ \ を用いてよい。グラフの凹凸は調べなくてよい。$
$(4)\ \ 2 \leqq m < n \ \ を満たす整数 \ m,\ n\ の組 \ (m,\ n)\ に対して、等式$
$ \hspace{5em} (*) \quad (2m-3)^n =(2n-3)^m$
$\quad が成り立つとする。このような組 \ (m,\ n)\ \ をすべて求めよ。$
\[\qquad \lim_{t \rightarrow \infty} \dfrac{\log t}{t}=0 \ \ の証明は\] $\hspace{3em}$不定形の極限値(1)$を参考にしてください。$
(1)
$f(x)=\cfrac{\log (2x-3)}{x} \quad より$
$f'(x)=\cfrac{\dfrac{2}{2x-3} \times x - \log(2x-3)}{x^2}=\cfrac{2x-(2x-3)\log(2x-3)}{x^2(2x-3)}$
$よって \quad g(x)=2x-(2x-3)\log(2x-3) $
(2)
$g(x)=2x-(2x-3)\log(2x-3) \quad より$
$g'(x)=2-2\log(2x-3)-(2x-3) \times \cfrac{2}{2x-3}=-2\log(2x-3)$
$x \geqq 2 \quad だから \quad 2x-3 \geqq 1 \quad よって \quad \log(2x-3)\geqq 0$
$ゆえに \quad g'(x) \leqq 0 \quad ただし等号は \ \ x=2\ \ のときのみ$
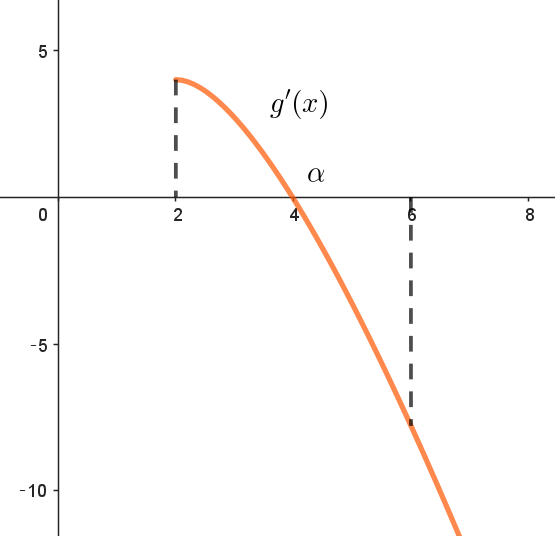
$g(x)\ \ は \ \ x \geqq 2 \ \ で単調減少$
$g(2)=4$
$g(6)=12-9\log 9 =12-18\log 3$
$ 2 < e < 3 \quad より \quad \log 3 > \log e =1 \quad だから \quad 12-18\log 3 <0$
$したがって \quad g(6) < 0$
$g(x) \ は連続関数だから中間値の定理より、区間 \ (2,\ 6)\ において$
$ g(\alpha)=0 \ \ を満たす \ 2\ 以上の実数 \ \alpha \ がただ \ 1\ つ存在する。$
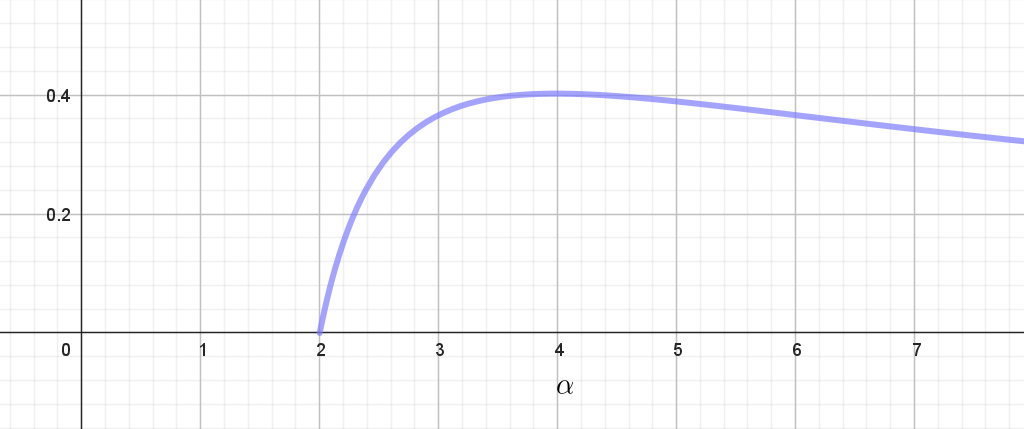
(3)
$増減表$
\[ \begin{array}{c||c|c|c|c|c} x& 2 & \cdots & \alpha & \cdots \\ \hline f'(x) & & + & 0 & - \\ \hline f(x) & & \nearrow & 極大 & \searrow & \\ \end{array} \]
\begin{eqnarray*}
& &\lim_{x \rightarrow \infty} \cfrac{\log(2x-3)}{x}\\
\\
&=&\lim_{x \rightarrow \infty} \cfrac{2x-3}{x} \times \cfrac{\log(2x-3)}{2x-3}\\
\\
&=&\lim_{x \rightarrow \infty} \big(2-\cfrac{3}{x}\big) \times \cfrac{\log(2x-3)}{2x-3}\\
\\
&=&2 \times 0\\
\\
&=&0
\end{eqnarray*}
$よって \quad x\ 軸は漸近線$
$f(2)=\cfrac{\log 1}{2}=0$
$y=f(x)\ のグラフは右図のとおり$
(4)
$(2m-3)^n =(2n-3)^m \quad の両辺の対数をとって$
$n\log(2m-3)=m\log(2n-3)$
$両辺を \ mn\ で割って$
$\cfrac{\log(2m-3)}{m}=\cfrac{\log(2n-3)}{n}$
$これは、f(x)=\cfrac{\log(2x-3)}{x} \ \ において \ \ f(m)= f(n)\ \ を満たす \ \ 2 \leqq m < \alpha < n \ \ の整数を見つけることである。$
$ただし、\alpha \ は \ \ 2 < \alpha < 6 \ \ を満たす。$
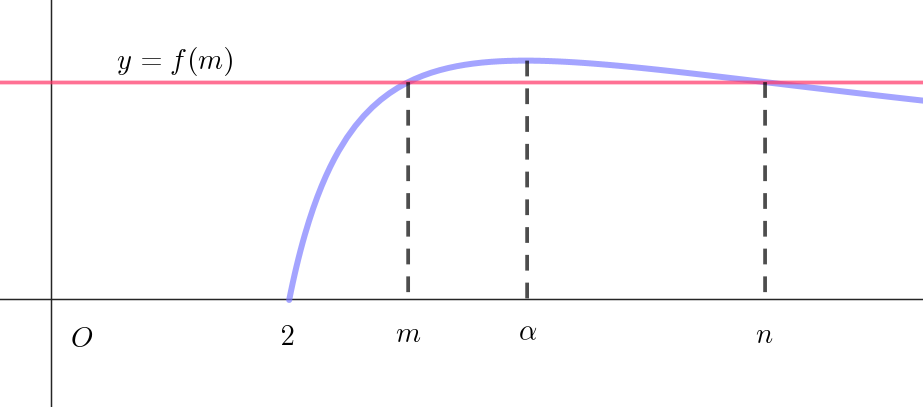
$f(m)=f(n)\ \ を満たす \ m,\ n\ は \ y=f(x)\ と$
$y=f(m)\ のグラフの交点の \ x\ 座標である。$
$明らかに \ \ 2 < m < \alpha ,\quad \alpha < n \quad であるが、$
$m\ が \ \alpha \ に近づけば、n\ も \ \alpha \ に近づく。$
(i)$\ \ m=2 \ \ のとき$
$\quad f(m)=0 \ \ であるが、f(n)=0 \ \ となる整数 \ n\ はない。$
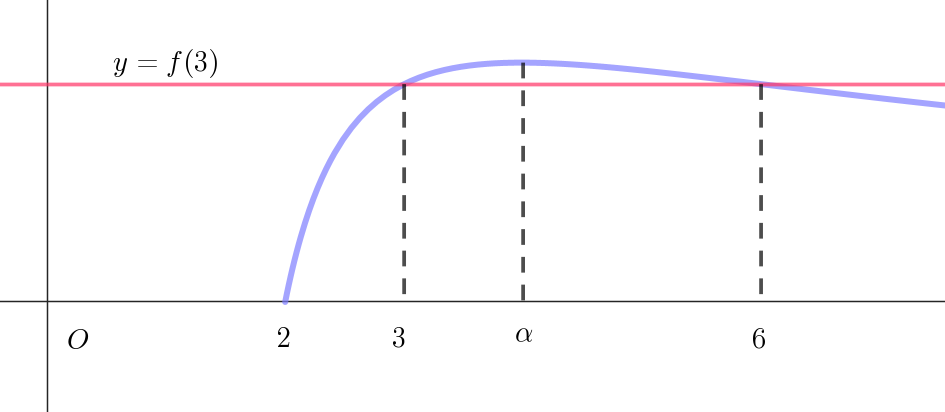
(ii)$\ \ m=3 \ \ のとき$
$\quad \cfrac{\log(2n-3)}{n}=\cfrac{\log 3}{3} \quad を満たす整数 \ n\ は$
$\quad \cfrac{\log(2n-3)}{n}=\cfrac{2\log 3}{6}=\cfrac{\log 9}{6} \quad だから \ \ n=6$
(iii)$\ \ m=4 \ \ のとき$
$\quad f(n)=f(4) \quad を満たす \ n\ は \ \ 4 < \alpha < n < 6 \ \ であるから \quad n=5$
$\quad ところが、\cfrac{\log(2 \times 5-3)}{5}=\cfrac{\log 7}{5} \ne \cfrac{\log 5}{4} \quad だから \ \ n=5\ \ は不適$
$\quad あるいは \quad (2m-3)^n=5^5 \qquad (2n-3)^m=7^4 \qquad 5^5 \ne 7^4 \quad だから \ \ m=4,\ \ n=5\ \ は不適でもよい$
(iv)$\ \ m=5 \ \ のとき$
$\quad 5 < \alpha < n < 6 \ \ を満たす整数 \ n\ は存在しない。$
$以上より、(m,\ n)=(3,\ 6)\ \ のみ$
メインメニュー に戻る