東北大学(理系) 2024年 問題4
$xyz\ 空間において、点P_1(3,\ -1,\ 1)\ を中心とし半径が \ \sqrt{5}\ の球面 S_1 \ と点P_2(5,\ 0,\ -1)\ を中心とし半径が$
$ \ \sqrt{2} \ の球面 \ S_2\ を考える。$
$(1)\ \ 線分 \ P_1P_2\ の長さを求めよ。$
$(2)\ \ S_1\ と \ S_2\ が交わりをもつことを示せ。この交わりは円となる。この円を \ C\ とし、その中心を \ P_3\ とする。$
$\quad C\ の半径および中心 \ P_3\ の座標を求めよ。$
$(3)\ \ (2)の円 \ C\ に対し、C\ を含む平面を \ H\ とする。xy\ 平面と \ H\ の両方に平行で、大きさが \ 1\ のベクトルを$
$\quad すべて求めよ。$
$(4)\ \ 点Q\ が(2)の円 \ C\ 上を動くとき、Q\ と \ xy\ 平面の距離 \ d\ の最大値を求めよ。また、d\ の最大値を与える$
$\quad 点Q\ の座標を求めよ。$
(1)
$P_1P_2=\sqrt{(5-3)^2+(0+1)^2+(-1-1)^2}=\sqrt{9}=3$
(2)
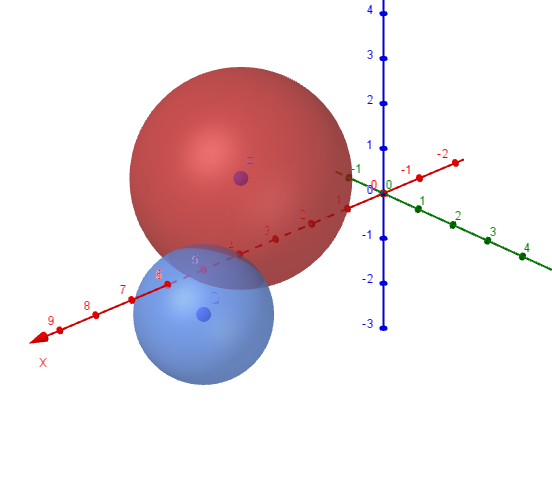
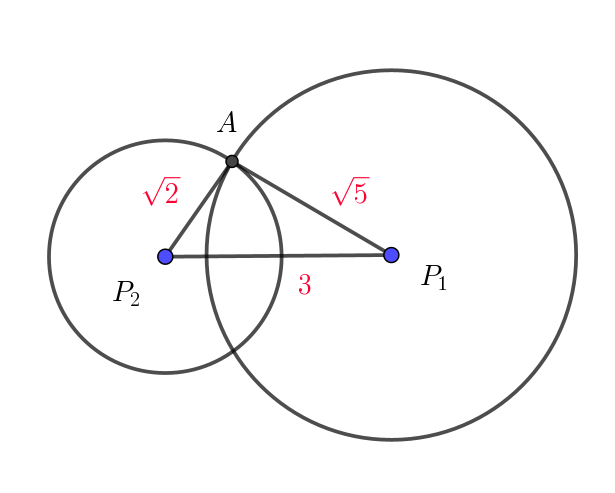
$右図は \ 2\ 球の交わり上の \ 1\ 点を \ A\ とし、線分 \ P_1P_2\ を水平にした図である。$
\begin{eqnarray*} & &(AP_1+AP_2)^2-P_1P_2^2\\ \\ &=&(\sqrt{5}+\sqrt{2})^2-3^2\\ \\ &=&2\sqrt{10}-2\\ \\ &=&2(\sqrt{10}-1)\\ \\ &>&0 \end{eqnarray*} $(AP_1+AP_2)^2 >P_1P_2^2$
$AP_1+AP_2 >P_1P_2 \quad だから \quad \ S_1\ と \ S_2\ は交わりをもつ。$
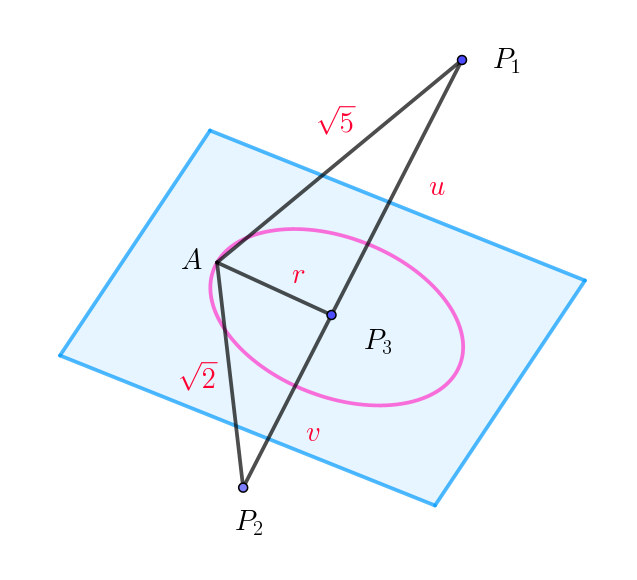
$右図のように、円 \ C\ 上の点を \ A,\ \ P_1P_3=u,\ \ P_2P_3=v\ \ とおくと$
$AP_3 \perp P_1P_2 \quad だから $
\[
\hspace{1em}
\left\{ \begin{array}{l}
u+v=3 \hspace{5.7em}(1)\\
r^2+u^2=5 \hspace{5em}(2)\\
r^2+v^2=2 \hspace{5em}(3)\\
\end{array} \right.
\]
$①を③に代入して \quad r^2+(3-u)^2=2$
$r^2+u^2-6u+9=2$
$②を代入して \quad 5-6u+9=2 \qquad u=2$
$したがって \quad v=1,\quad r=1$
$点P_3 (x,\ y,\ z)\ は線分 \ P_1P_2\ を \ u:v=2:1 \ に内分する点だから$
$x=\cfrac{2 \times 5+1 \times 3}{3}=\cfrac{13}{3}, \quad y=\cfrac{2 \times 0+1 \times (-1)}{3}=-\cfrac{1}{3},\quad z=\cfrac{2 \times (-1)+1 \times 1}{3}=-\cfrac{1}{3}$
$よって \quad P_3(\cfrac{13}{3},\ -\cfrac{1}{3},\ -\cfrac{1}{3})$
$(別解)$
$S_1\ と \ S_2\ の交わりは$
\[
\hspace{1em}
\left\{ \begin{array}{l}
(x-3)^2+(y+1)^2+(z-1)^2=5 \hspace{5em}④\\
(x-5)^2+y^2+(z+1)^2=2 \hspace{7.5em}⑤\\
\end{array} \right.
\]
$④-⑤ \quad より \quad 4x+2y-4z=18$
$\therefore \ \ 2x+y-2z=9 \quad これは円 \ C\ を含む平面である。$
$直線 \ P_1P_2 \ の方向ベクトルは $
$\vec{d}=\vec{OP_2}-\vec{OP_1}=(5,0,-1)-(3,-1,1)=(2,1,-2)$
$直線 \ P_1P_2\ のベクトル方程式は \quad \vec{OP}=\vec{OP_1}+t\vec{d}=(3,\ -1,\ 1)+t(2,\ 1,\ -2)=(3+2t,\ -1+t,\ 1-2t)$
$直線 \ P_1P_2\ と平面 \ 2x+y-2z=9 \ の交点が円 \ C\ の中心 \ P_3\ だから $
$2(3+2t)+(-1+t)-2(1-2t)=9 \qquad \therefore \ \ t=\cfrac{2}{3}$
$\vec{OP_3}=(3+2 \times \cfrac{2}{3},\ -1+\cfrac{2}{3},\ 1-2 \times \cfrac{2}{3})=(\cfrac{13}{3},\ -\cfrac{1}{3},\ -\cfrac{1}{3})$
(3)
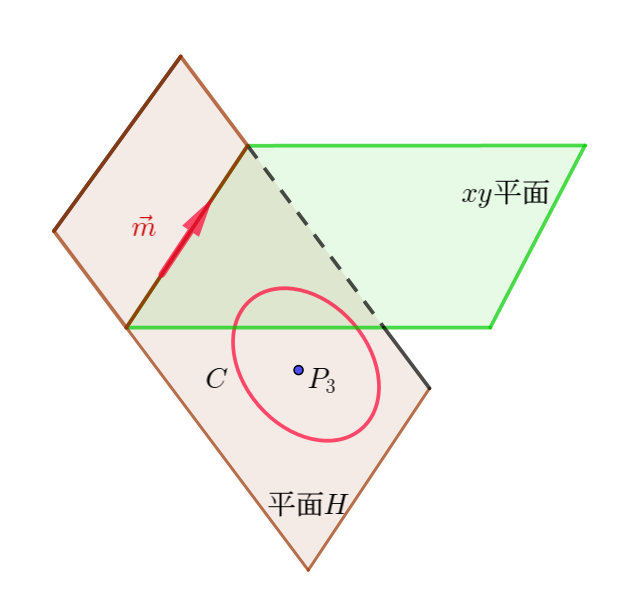
$求めるベクトルを \quad \vec{m}=(a,\ b,\ c) \quad とすると$
(i)$\ \ \vec{m} /\!/ xy 平面 \quad だから \quad \vec{m} \perp z\ 軸$
$\quad (a,\ b,\ c) \cdot (0,\ 0,\ 1)=0 \qquad c=0$
(ii)$\ \ \vec{m} /\!/ 平面 H \quad だから$
$\quad \vec{m} \ は平面 \ H\ の法線ベクトル \ (2,\ 1,\ -2)\ に垂直$
$\quad (a,\ b,\ 0) \cdot (2,\ 1,\ -2)=0 $
$\quad 2a+b=0 \qquad b=-2a$
$\quad \vec{m}=(a,\ -2a,\ 0)=a(1,\ -2,\ 0)$
$\quad |\vec{m}|=|a| \sqrt{1^2+(-2)^2}=\sqrt{5} |a|$
$よって、大きさが \ 1\ の単位ベクトルは \quad \cfrac{1}{\sqrt{5}}(1,\ -2,\ 0),\quad -\cfrac{1}{\sqrt{5}}(1,\ -2,\ 0)$
$なお、\vec{m}\ は平面 \ H\ と \ xy\ 平面の交線に平行である。$
(4)
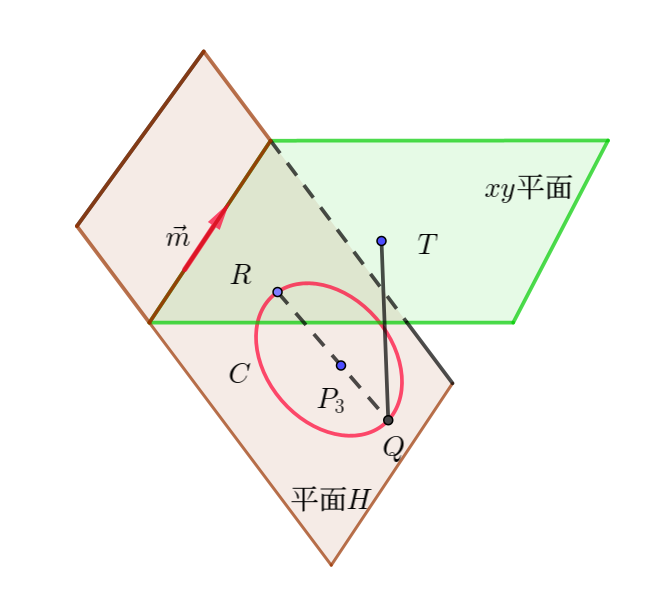
$Q(x,\ y,\ z)\ は$
$平面 \ H\ 上にあるから \quad 2x+y-2z=9 \hspace{13em}⑦$
$円 \ C\ 上にあるから \quad (x-\dfrac{13}{3})^2+(y+\dfrac{1}{3})^2+(z+\dfrac{1}{3})^2=1 \hspace{5em}⑧$
$\vec{P_3Q}=(x,\ y,\ z)-(\dfrac{13}{3} ,\ -\dfrac{1}{3} , \ -\dfrac{1}{3}) =(x-\dfrac{13}{3}, \ y+\dfrac{1}{3}, \ z+\dfrac{1}{3})$
$円\ C\ の直径を \ QR\ とすると、線分 \ QR\ が(3)の \ \vec{m}\ に直交するとき、$
$点Q\ と \ xy\ 平面の距離 \ d\ は最大となる。$
$\vec{P_3Q} \perp \vec{m} \quad だから \quad (x-\dfrac{13}{3}, \ y+\dfrac{1}{3}, \ z+\dfrac{1}{3}) \cdot (1,\ -2,\ 0)=0$
$(x-\dfrac{13}{3}) -2(y+\dfrac{1}{3})=0 \hspace{19em}⑨$
$⑨より \quad x=2y+5$
$⑦に代入して \quad 2(2y+5)+y-2z=9$
$z=\dfrac{5}{2}y+\dfrac{1}{2}$
$x,\ z\ を⑧に代入して$
$(2y+5-\dfrac{13}{3})^2+(y+\dfrac{1}{3})^2+(\dfrac{5}{2}y+\dfrac{1}{2}+\dfrac{1}{3})^2=1$
$(2y+\dfrac{2}{3})^2+(y+\dfrac{1}{3})^2+(\dfrac{5}{2}y+\dfrac{5}{6})^2=1$
$4(y+\dfrac{1}{3})^2+(y+\dfrac{1}{3})^2+\dfrac{25}{4}(y+\dfrac{1}{3})^2=1$
$\dfrac{45}{4} (y+\dfrac{1}{3})^2 =1$
$(y+\dfrac{1}{3})^2 =\dfrac{4}{45}$
$y=-\dfrac{1}{3} \pm \dfrac{2}{3\sqrt{5}}=\dfrac{-5 \pm 2\sqrt{5}}{15}$
(i)$\ \ y=\dfrac{-5 + 2\sqrt{5}}{15} \quad のとき$
$\quad z=\dfrac{5}{2} \times \dfrac{-5 + 2\sqrt{5}}{15} +\dfrac{1}{2}=\cfrac{-1+\sqrt{5}}{3}>0$
$\quad x=2 \times \dfrac{-5 + 2\sqrt{5}}{15} +5= \cfrac{65+4\sqrt{5}}{15}$
$\quad これは点R\ の座標である。このとき \quad d=z=\cfrac{-1+\sqrt{5}}{3}$
(ii)$\ \ y=\dfrac{-5 - 2\sqrt{5}}{15} \quad のとき$
$\quad z=\dfrac{5}{2} \times \dfrac{-5 - 2\sqrt{5}}{15} +\dfrac{1}{2}=\cfrac{-1-\sqrt{5}}{3}<0$
$\quad x=2 \times \dfrac{-5 - 2\sqrt{5}}{15} +5=\cfrac{65-4\sqrt{5}}{15}$
$\quad これが点Q\ の座標である。$
$よって \quad Q(\cfrac{65-4\sqrt{5}}{15},\ \dfrac{-5 - 2\sqrt{5}}{15},\ \cfrac{-1-\sqrt{5}}{3})$
$このとき 、d\ の最大値は \quad d=-z=\cfrac{1+\sqrt{5}}{3}$
メインメニュー に戻る