東北大学(理系) 2024年 問題3
$n\ を \ 2\ 以上の整数とする。それぞれ \ A,\ A,\ B\ と書かれた \ 3\ 枚のカードから無作為に \ 1\ 枚抜き出し、カードを$
$もとに戻す試行を考える。この試行を \ n\ 回繰り返し、抜き出したカードの文字を順に左から右に並べ、n\ 文$
$字の文字列を作る。作った文字列内に \ AAA\ の並びがある場合は不可とする。また、作った文字列内に \ BB$
$の並びがある場合も不可とする。これらの場合以外は可とする。たとえば \ n=6\ のとき、文字列 \ AAAABA$
$や \ ABBBAA \ や \ ABBABB \ や \ BBBAAA\ などは不可で、文字列 \ BABAAB \ や \ BABABA\ などは可である。$
$作った文字列が可でかつ右端の \ 2\ 文字が \ AA\ である確率を \ p_n,\ 作った文字列が可でかつ右端の \ 2\ 文字が \ BA$
$である確率を \ q_n、作った文字列が可でかつ右端の文字が \ B\ である確率を \ r_n\ とそれぞれおく。$
$(1)\ \ p_2,\ \ q_2,\ \ r_2\ をそれぞれ求めよ。また、p_{n+1},\ \ q_{n+1},\ \ r_{n+1}\ \ を \ p_n,\ \ q_n,\ \ r_n \ \ を用いてそれぞれ表せ。$
$(2)\ \ p_n+2q_n+2r_n \ \ を \ \ n\ を用いて表せ。$
$(3)\ \ p_n+iq_n-(1+i)r_n \ \ を \ n\ を用いて表せ。ただし、i\ は虚数単位である。$
$(4)\ \ p_n=r_n \ \ を満たすための、n\ の必要十分条件を求めよ。$
(1)
$3\ 枚のカードから1\ 枚抜き出し、もとに戻す試行だからこれは独立試行である。$
$したがって、A\ と書かれたカードが抜き出される確率は \ \ \cfrac{2}{3},\ \ B\ と書かれたカードが抜き出される確率は \ \ \cfrac{1}{3}\ \ である。$
$2\ 回の試行で作られた文字列が$
$AA\ となる事象の確率が \ p_2 \ だから \quad p_2=\cfrac{2}{3} \times \cfrac{2}{3}=\cfrac{4}{9}$
$BA\ となる事象の確率が \ q_2 \ だから \quad q_2=\cfrac{1}{3} \times \cfrac{2}{3}=\cfrac{2}{9}$
$作った文字列が可でかつ右端の文字が \ B\ となるのは \ AB\ であるからこの事象の確率\ r_2\ は \quad r_2=\cfrac{2}{3} \times \cfrac{1}{3}=\cfrac{2}{9}$
$n\ 回の試行で作られた可である文字列の右端の \ 2\ 文字が \ AA\ である事象を \ P_n,\ \ BA\ である事象を \ Q_n,$
$右端の \ 1\ 文字が \ B\ である事象を \ R_n\ とする。$
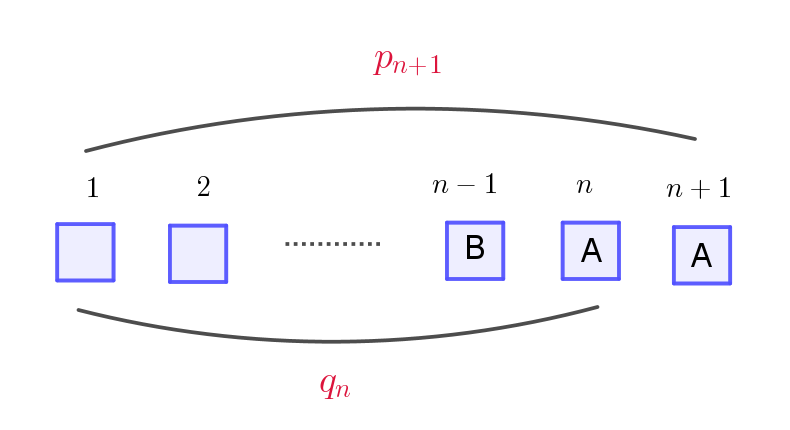
$事象 \ P_{n+1}\ は \ n-1\ 回目は \ B\ が抜き出されなくては$
$ならない。これは事象 \ Q_n\ に引き続き、A\ が抜き出さ$
$れることと同じであるから$
$\quad p_{n+1}=q_n \times \cfrac{2}{3}=\cfrac{2}{3}q_n$
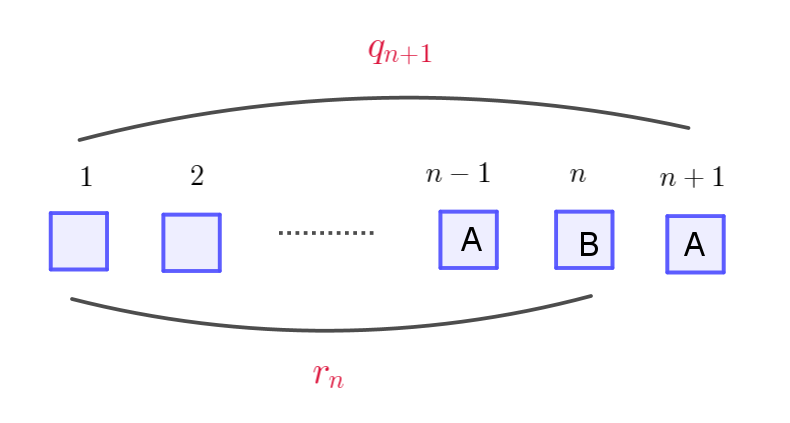
$事象\ Q_{n+1}\ は \ n-1\ 回目は \ A\ が抜き出されなくては$
$ならない。これは事象 \ R_n \ に引き続き、A\ が抜き出さ$
$れることと同じであるから$
$\quad q_{n+1}=r_n \times \cfrac{2}{3}=\cfrac{2}{3}r_n$
$事象 \ R_{n+1}\ は \ n\ 回目に \ A,\ n+1\ 回目に \ B\ が抜き出されるから$
$n-1\ 回目は \ A\ が抜き出される場合と \ B\ が抜き出される場合がある。$
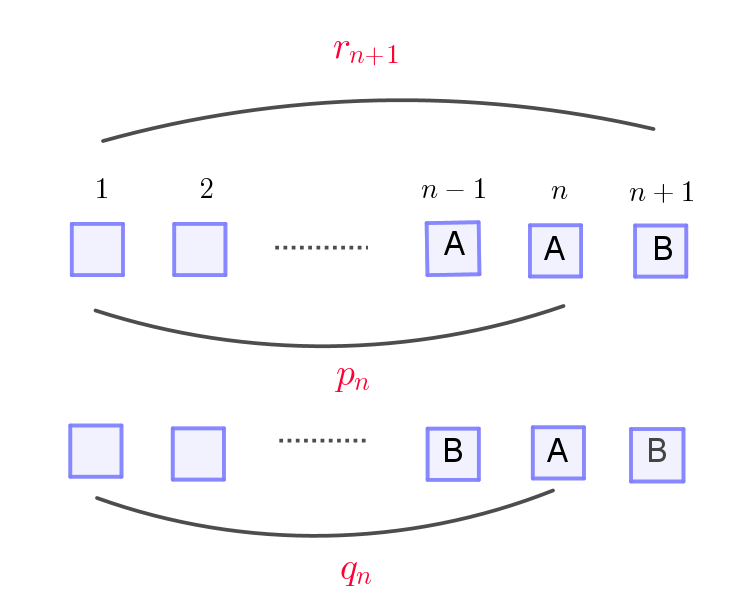
(i)$\ \ Aが抜き出される場合は$
$\quad 事象\ P_n \ に引き続き、B\ が抜き出されることと同じ$
$\quad である。$
(ii)$\ \ Bが抜き出される場合は$
$\quad 事象 \ Q_n \ に引き続き、B\ が抜き出されることと同じ$
$\quad である。$
(i),(ii)$\ \ は互いに排反であるから$
$\quad r_{n+1}=p_n \times \cfrac{1}{3}+q_n \times \cfrac{1}{3}=\cfrac{1}{3}(p_n+q_n)$
(2)
$s_n=p_n+2q_n+2r_n \quad とおくと(1)より$
\begin{eqnarray*} s_{n+1} &=&p_{n+1}+2q_{n+1}+2r_{n+1}\\ \\ &=&\cfrac{2}{3}q_n+\cfrac{4}{3}r_n+\cfrac{2}{3}(p_n+q_n)\\ \\ &=&\cfrac{2}{3}p_n+\cfrac{4}{3}q_n+\cfrac{4}{3}r_n\\ \\ &=&\cfrac{2}{3}(p_n+2q_n+2r_n)\\ \\ &=&\cfrac{2}{3}s_n \end{eqnarray*}
$s_2=p_2+2q_2+2r_2=\cfrac{4}{9}+2 \times \cfrac{2}{9}+ 2 \times \cfrac{2}{9}=\cfrac{4}{3} \quad だから$
$s_n=\cfrac{4}{3} \times \big(\cfrac{2}{3}\big)^{n-2}=2\big(\cfrac{2}{3}\big)^{n-1}$
$よって \quad n \geqq 2 \ \ のとき \quad p_n+2q_n+2r_n =2\big(\cfrac{2}{3}\big)^{n-1}$
(3)
$t_n=p_n+iq_n-(1+i)r_n \quad とおくと(1)より$
\begin{eqnarray*} t_{n+1} &=&p_{n+1}+iq_{n+1}-(1+i)r_{n+1}\\ \\ &=&\cfrac{2}{3}q_n+i \times \cfrac{2}{3}r_n -(1+i) \times \cfrac{1}{3}(p_n+q_n)\\ \\ &=&-\cfrac{1+i}{3}p_n+\cfrac{1-i}{3}q_n+\cfrac{2}{3}ir_n\\ \\ &=&-\cfrac{1+i}{3}\big(p_n -\cfrac{1-i}{1+i}q_n -\cfrac{2i}{1+i}r_n\big)\\ \\ &=&-\cfrac{1+i}{3}\big(p_n +iq_n -(1+i)r_n\big)\\ \\ &=&-\cfrac{1+i}{3}t_n \end{eqnarray*}
$t_2=p_2+iq_2-(1+i)r_2=\cfrac{4}{9}+\cfrac{2}{9}i -(1+i) \times \cfrac{2}{9}=\cfrac{2}{9} \quad だから $
$t_n=\cfrac{2}{9}\big(-\cfrac{1+i}{3}\big)^{n-2}$
$よって \quad n \geqq 2 \ \ のとき \quad p_n+iq_n-(1+i)r_n =\cfrac{2}{9}\big(-\cfrac{1+i}{3}\big)^{n-2}$
(4)
$(3)で得られた \quad p_n+iq_n-(1+i)r_n =\cfrac{2}{9}\big(-\cfrac{1+i}{3}\big)^{n-2}\quad において \quad p_n=r_n \quad とおくと$
$ p_n+iq_n-(1+i)p_n =\cfrac{2}{9}\big(-\cfrac{1+i}{3}\big)^{n-2}$
$-i(p_n-q_n) =\cfrac{2}{9}\big(-\cfrac{1+i}{3}\big)^{n-2}$
\begin{eqnarray*} 右辺 &=&\cfrac{2}{9}\big(-\cfrac{1}{3}\big)^{n-2}(1+i)^{n-2}\\ \\ &=&\cfrac{2}{9}\big(-\cfrac{1}{3}\big)^{n-2} \times \big\{\sqrt{2}\big(\cos \dfrac{\pi}{4}+i\sin \dfrac{\pi}{4}\big)\big\}^{n-2}\\ \\ &=&\cfrac{2}{9}\big(-\cfrac{1}{3}\big)^{n-2} \sqrt{2}^{n-2}\big(\cos \dfrac{n-2}{4}\pi+i\sin \dfrac{n-2}{4}\pi\big)\\ \end{eqnarray*}
$左辺は純虚数だから、右辺の実部は \ 0\ である。$
$\cos \dfrac{n-2}{4}\pi=0$
$\cfrac{n-2}{4}\pi=\cfrac{\pi}{2}+k\pi\ \ (k\ は整数)$
$n-2=2+4k$
$n=4(k+1) \quad だから \quad n\ は \ 4\ の倍数$
$逆に、n=4(k+1)\ \ ならば逆にたどって \ \ p_n=r_n \ \ がいえるから$
$p_n=r_n \ \ を満たすための、n\ の必要十分条件は \ \ n\ は \ 4\ の倍数である。$
$(補充)$
$逆が不安な場合には、次のようにすればよいでしょう。$
$p_n+iq_n-(1+i)r_n =\cfrac{2}{9}\big(-\cfrac{1+i}{3}\big)^{n-2}\quad において \quad n=4(k+1) \quad のとき$
\begin{eqnarray*} 右辺 &=&\cfrac{2}{9}\big(-\cfrac{1+i}{3}\big)^{4k+2}\\ \\ &=&\cfrac{2}{9}\big(-\cfrac{1+i}{3}\big)^2 \big\{\big(-\cfrac{1+i}{3}\big)^4 \big\}^k\\ \\ &=&\cfrac{2}{9}\big(\cfrac{2i}{9}\big)\big(\cfrac{-4}{81}\big)^k\\ \end{eqnarray*} $これは純虚数である。$
$左辺=p_{4(k+1)}+iq_{4(k+1)}-(1+i)r_{4(k+1)}=(p_{4(k+1)}- r_{4(k+1)})+i(q_{4k+2}-r_{4(k+1)}) $
$これが純虚数になるのは、p_{4(k+1)}=r_{4(k+1)} \quad のときである。$
$(研究)$
$設問(2)と(3)で用いられている漸化式はどのようにして得られたのか考えてみましょう。$
$s_n=p_n+aq_n+br_n \ \ (a,\ b\ は定数)\ \ の漸化式をつくります。$
\begin{eqnarray*} s_{n+1} &=&p_{n+1}+aq_{n+1}+br_{n+1}\\ \\ &=&\cfrac{2}{3}q_n+\cfrac{2}{3}ar_n+\cfrac{1}{3}b(p_n+q_n)\\ \\ &=&\cfrac{b}{3}p_n+\big(\cfrac{2}{3}+\cfrac{b}{3}\big)q_n+\cfrac{2}{3}ar_n\\ \\ &=&\cfrac{b}{3}\big(p_n+\cfrac{b+2}{b}q_n+\cfrac{2a}{b}r_n\big)\\ \end{eqnarray*} \[ ここで、 \hspace{1em} \left\{ \begin{array}{l} a=\cfrac{b+2}{b} \hspace{5em}①\\ b=\cfrac{2a}{b} \hspace{6em}②\\ \end{array} \right. \] $が成りたつとすると$
$②より \quad a=\cfrac{b^2}{2} $
$①に代入して \quad \cfrac{b^2}{2}=\cfrac{b+2}{b} \qquad b^3-2b-4=0$
$因数分解して \quad (b-2)(b^2+2b+2)=0$
$これを解いて \quad b=2,\ \ -1 \pm i$
$①より \quad a=1+\cfrac{2}{b} \quad だからこれに代入して$
(i)$\ \ b=2 \quad のとき \quad a=1+\cfrac{2}{2}=2 \quad だから$
$\quad s_{n}=p_n+2q_n+2r_n , \qquad s_{n+1}=\cfrac{2}{3}s_n \quad が得られます。$
(ii)$\ \ b=-1-i \quad のとき \quad a=1+\cfrac{2}{-1-i}=i \quad だから$
$\quad s_{n}=p_n+iq_n-(1+i)r_n , \qquad s_{n+1}=-\cfrac{1+i}{3}s_n \quad が得られます。$
$これらが問題に使われた漸化式です。$
$なお$
(iii)$\ \ b=-1+i \quad のとき \quad a=1+\cfrac{2}{-1+i}=-i \quad だから$
$\quad s_{n}=p_n-iq_n-(1-i)r_n ,\qquad s_{n+1}=-\cfrac{1-i}{3}s_n \quad が得られます。$
$これを設問にする手もあったと思われますが、いかがでしょうか。$
メインメニュー に戻る