MY MATH NOTE

東北大学(理系) 2024年　問題1

$a\ を正の実数とし、f(x)=x^2-2ax+4a^2 \ \ とする。O\ を原点とする \ xy\ 平面上の放物線 \ C:y=f(x)\ \ の$
$頂点を \ A\ とする。直線 \ OA\ と \ C\ の交点のうち、A\ と異なるものを \ P(p,\ f(p))\ とし、O\ から \ C\ へ引いた$
$接線の接点を \ Q(q,\ f(q))\ とする。ただし、q > 0\ とする。$
$(1)\ \ p,\ q\ の値を \ a\ を用いて表せ。また、p > q\ \ であることを示せ。$
$(2)\ \ 放物線 \ C\ の \ q \leqq x \leqq p \ \ の部分、線分 \ OP 、および線分 \ OQ\ で囲まれた図形の面積を \ S\ とおく。$
$\quad S\ を \ a\ を用いて表せ。$
$(3)\ \ (2)のSに対し、S=\dfrac{2}{3} となるときのaの値を求めよ。$

(1)

　
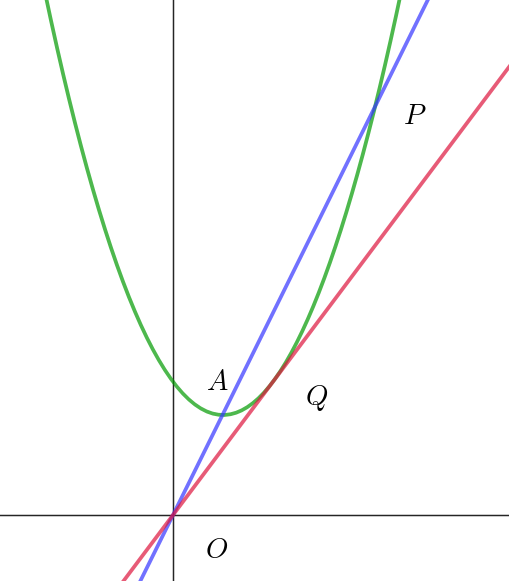
$f(x)=x^2-2ax+4a^2=(x-a)^2+3a^2 \quad だから \quad A(a,\ 3a^2)$

$直線 \ OA\ は \ \ y=\cfrac{3a^2}{a}x \quad よって \quad y=3ax$

$直線 \ OA\ と \ C\ の交点は $

$x^2-2ax+4a^2=3ax \quad を解いて$

$x^2-5ax+4a^2=0 \qquad (x-a)(x-4a)=0$

$x \ne a \quad だから \quad x=4a \qquad よって \quad p=4a$

$f'(x)=2x-2a \quad だから \ 点Q(q,\ f(q))\ における接線は$

$y=(2q-2a)(x-q)+q^2-2aq+4a^2$

$y=(2q-2a)x-q^2+4a^2$

$これが原点を通るから \quad -q^2+4a^2=0$

$q^2=4a^2 \quad a > 0,\ \ q > 0 \quad だから \quad q=2a$

$このとき$

$p-q=4a-2a=2a > 0 \quad だから \quad p > q$

(2)

　
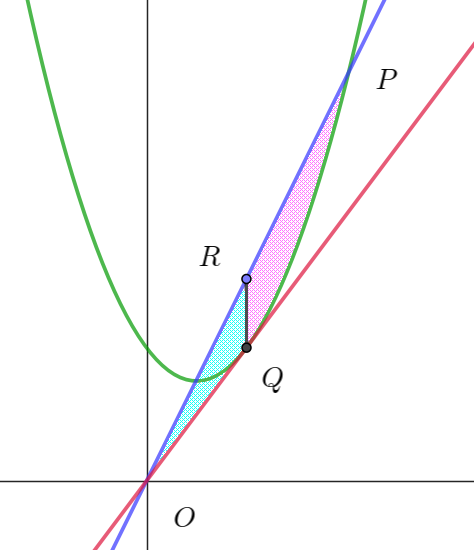
$x=2a\ \ である直線 \ OA\ 上の点を \ R\ とすると \quad R(2a,\ 6a^2)$

$点Q\ の \ y\ 座標は$

$y=2(2a-a)(2a)-(2a)^2+4a^2=4a^2 \quad だから \quad Q(2a,\ 4a^2)$

$QR=6a^2-4a^2=2a^2$

$\triangle OQR=\cfrac{1}{2} \times 2a^2 \times 2a=2a^3$

\begin{eqnarray*} S &=&\triangle OQR + \int_{2a}^{4a}\big(3ax-(x^2-2ax+4a^2)\big)dx\\ \\ &=&2a^3 + \int_{2a}^{4a}(-x^2+5ax-4a^2)dx\\ \\ &=&2a^3 + \big[-\dfrac{x^3}{3}+\cfrac{5a}{2}x^2-4a^2x\big]_{2a}^{4a}\\ \\ &=&2a^3 + \big(-\dfrac{64}{3}a^3+40a^3-16a^3\big) -\big(-\cfrac{8}{3}a^3 +10a^3-8a^3\big )\\ \\ &=&\cfrac{16}{3}a^3 \end{eqnarray*}

(3)

ページの先頭へ↑