静岡大学(理系) 2024年 問題4
$空間内に点 \ O,\ A,\ B,\ C,\ D,\ E\ がある。3\ 点 \ O,\ B,\ C\ は一直線上にないとし、これら \ 3\ 点を含む平面を \ \alpha $
$とする。平面 \ \alpha \ はベクトル \ \vec{OA}\ に垂直であり、\vec{OA} \ne \vec{0},\ \ \vec{BD}=s\vec{OA},\ \ \vec{CE}=t\vec{OA}\ \ (0 < t < s < 1)\ \ を満たし$
$ている。また、2\ 点 \ A,\ D\ を通る直線、2\ 点 \ D,\ E\ を通る直線、2\ 点 \ A,\ E\ を通る直線が平面 \ \alpha \ と交わる点を$
$それぞれ \ P,\ Q,\ R\ とする。\vec{OA}=\vec{a},\ \ \vec{OB}=\vec{b},\ \ \vec{OC}=\vec{c}\ \ とするとき、次の問いに答えよ。$
$(1)\ \ \vec{OP}\ を \ \vec{b}\ と実数 \ s\ を用いて表せ。$
$(2)\ \ \vec{OQ}\ を \ \vec{b},\ \ \vec{c} \ \ および実数 \ s,\ t\ を用いて表せ。$
$(3)\ \ 3点 \ P,\ Q,\ R\ が一直線上にあることを示せ。$
(1)
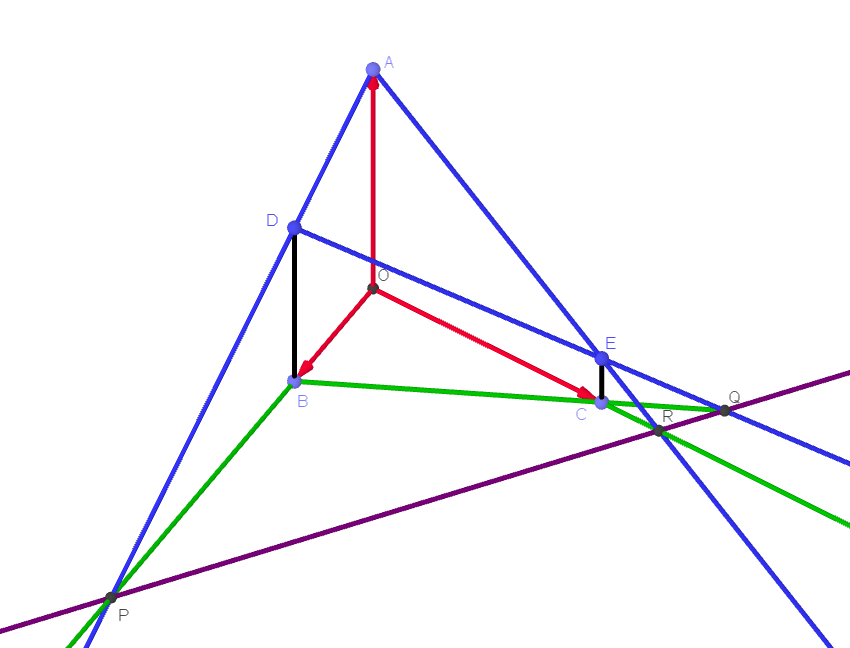
$直線AD\ は平行な \ 2\ 直線 \ OA,\ BD\ がつくる平面OADB$
$上にある。$
$点P\ は直線AD\ 上にあるから、この平面上の点である。$
$また点P\ は平面 \ \alpha \ 上にもあるから、点P\ は \ 2\ 平面の交線$
$OB\ にある。$
$\triangle PAO \sim \triangle PDB \ \ だから$
$PO:PB=OA:BD=1:s$
$sPO=PB \quad よって \quad s\vec{PO}=\vec{PB}$
$-s\vec{OP}=\vec{OB}-\vec{OP}$
$(1-s)\vec{OP}=\vec{OB}$
$\vec{OP}=\cfrac{1}{1-s}\vec{b}$
(2)
$\vec{CE}=t\vec{OA}\ \ より \ \ CE /\!/ OA$
$(1)より \ \ BD /\!/ OA \ \ だから \ \ CE /\!/ BD$
$直線DE\ は平行な \ 2\ 直線 \ CE,\ BD\ がつくる平面DBCE \ 上にある。$
$点Q\ は直線DE\ 上にあるから、この平面上の点である。$
$また点Q\ は平面 \ \alpha \ 上にもあるから、点Qは2\ 平面の交線BC\ にある。$
$BD=sOA, \quad CE=tOA \ \ より \ \ BD:CE=s:t$
$\triangle QDB \sim \triangle QEC \quad だから$
$QB:QC=BD:CE=s:t$
$tQB=sQC \quad よって \quad t\vec{QB}=s\vec{QC}$
$t(\vec{OB}-\vec{OQ})=s(\vec{OC}-\vec{OQ})$
$(s-t)\vec{OQ}=-t\vec{OB}+s\vec{OC}$
$\vec{OQ}=-\cfrac{t}{s-t}\vec{b}+\cfrac{s}{s-t} \vec{c}$
(3)
$直線AE\ は平行な \ 2\ 直線 \ OA,\ CE\ がつくる平面OAEC\ 上にある。$
$点R\ は直線AE\ 上にあるから、この平面上の点である。$
$また、点R\ は平面 \ \alpha \ 上にもあるから、点R\ は \ 2\ 平面の交線OC\ にある。$
$\triangle ROA \sim \triangle RCE \quad だから$
$RO:RC=OA:CE=1:t$
$tRO=RC \quad よって \quad t\vec{RO}=\vec{RC}$
$-t\vec{OR}=\vec{OC}-\vec{OR}$
$(1-t)\vec{OR}=\vec{OC}$
$\vec{OR}=\cfrac{1}{1-t}\vec{c}$
$以上まとめると$
$\vec{OP}=\cfrac{1}{1-s}\vec{b},\quad \vec{OQ}=-\cfrac{t}{s-t}\vec{b}+\cfrac{s}{s-t} \vec{c},\quad \vec{OR}=\cfrac{1}{1-t}\vec{c}$
$したがって$
\begin{eqnarray*} \vec{PQ} &=&\vec{OQ}-\vec{OP}\\ \\ &=&-\cfrac{t}{s-t}\vec{b}+\cfrac{s}{s-t} \vec{c}-\cfrac{1}{1-s}\vec{b}\\ \\ &=&-\big(\cfrac{t}{s-t}+ \cfrac{1}{1-s}\big)\vec{b}+\cfrac{s}{s-t} \vec{c}\\ \\ &=&-\cfrac{s(1-t)}{(s-t)(1-s)}\vec{b}+\cfrac{s}{s-t} \vec{c}\\ \\ &=&\cfrac{s(1-t)}{s-t}\big(-\cfrac{1}{1-s}\vec{b}+\cfrac{1}{1-t} \vec{c}\big)\\ \\ &=&\cfrac{s(1-t)}{s-t}(-\vec{OP}+\vec{OR})\\ \\ &=&\cfrac{s(1-t)}{s-t}\vec{PR}\\ \end{eqnarray*} $よって\ \ 3点 \ P,\ Q,\ R\ は一直線上にある。$
メインメニュー に戻る