静岡大学(理系) 2024年 問題3
\[
関数 \ f(x\ ),\ g(x)\ を \ f(x)=x-x^2,
\hspace{2em}
g(x)=
\left\{ \begin{array}{l}
f(x) \hspace{3em} (0 \leqq x \leqq 1)\\
f(-x) \hspace{2em} (-1 \leqq x \leqq 0)\\
\end{array} \right.
\quad により定める。
\]
$曲線 \ y=g(x)\ および \ y=\cfrac{2}{\pi^2} \sin \pi x \ \ (-1 \leqq x \leqq 1)\ \ によって囲まれる図形 \ D\ を考える。このとき、$
$次の問いに答えよ。$
$(1)\ \ h(x)=f(x)-\cfrac{2}{\pi^2} \sin \pi x \ \ とおくとき、h(x)\ の \ x=\cfrac{1}{2}\ における微分係数を求めよ。$
$(2)\ \ 0 \leqq x \leqq 1 \ \ の範囲で \ \ f(x) \geqq \cfrac{2}{\pi^2} \sin \pi x \ \ が成り立つことを示せ。$
$(3)\ \ D\ の面積を求めよ。$
$(4)\ \ D\ を \ x\ 軸のまわりに \ 1\ 回転してできる回転体の体積を求めよ。$
(1)
$h(x)=f(x)-\cfrac{2}{\pi^2} \sin \pi x =x-x^2 -\cfrac{2}{\pi^2} \sin \pi x \quad より$
$h'(x)=1-2x -\cfrac{2}{\pi} \cos \pi x $
$h'(\dfrac{1}{2})=1-2 \times \cfrac{1}{2} -\cfrac{2}{\pi} \cos \dfrac{\pi}{2} =0$
(2)
$h(x)=f(x)-\cfrac{2}{\pi^2} \sin \pi x \quad とおくと$
$h'(x)=1-2x -\cfrac{2}{\pi} \cos \pi x $
$h''(x)=-2 + 2\sin \pi x=-2(1-\sin \pi x) \leqq 0$
$よって \ \ h'(x)\ は単調減少 \quad (1)より \quad h'(\dfrac{1}{2})=0 \quad だから$
$0 \leqq x \leqq \cfrac{1}{2} \quad のとき \ \ h'(x) >0 ,\quad \cfrac{1}{2} \leqq x \leqq 1 \quad のとき \ \ h'(x) <0$
$h(0)=0, \quad h(1)=0 $
$増減表は$
\[ \begin{array}{c||c|c|c|c|c} x& 0 & \cdots & \dfrac{1}{2} & \cdots & 1\\ \hline h'(x)& & + & 0 & - & \\ \hline h(x)& 0 & \nearrow & 極大 & \searrow & 0\\ \end{array} \]
$したがって \ \ 0 \leqq x \leqq 1 \ \ の範囲で \ \ h(x) \geqq 0 \ \ だから \quad f(x) \geqq \cfrac{2}{\pi^2} \sin \pi x \ \ が成り立つ。$
(3)
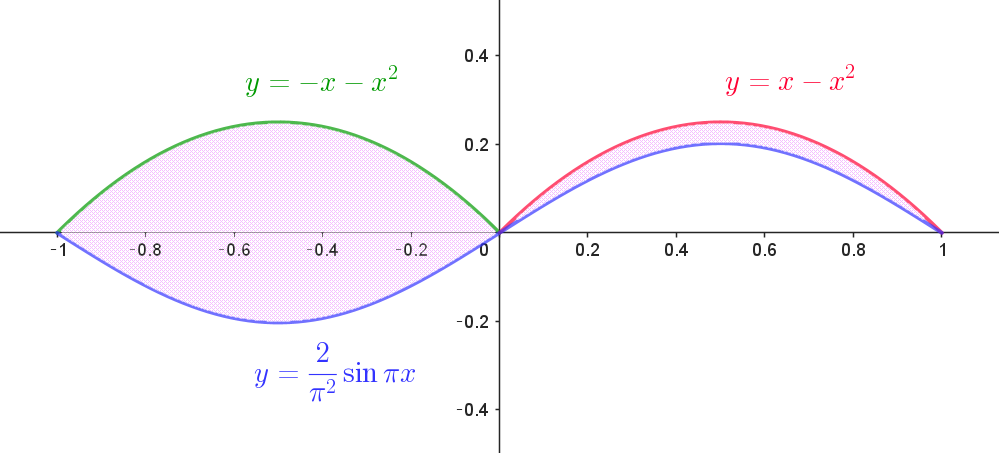
$f(x) \ と \ f(-x) \ のグラフは \ y\ 軸に関して対称であること$
$に留意してかいた領域 \ D\ が右図である。$
$この面積を \ S\ とすると$
\begin{eqnarray*} S &=&\int_{-1}^0(-x-x^2-\cfrac{2}{\pi^2} \sin \pi x )dx + \int _0^1(x-x^2-\cfrac{2}{\pi^2} \sin \pi x )dx\\ \\ &=&\int_{-1}^0(-x-x^2)dx + \int _0^1(x-x^2)dx - \int_{-1}^1 \cfrac{2}{\pi^2} \sin \pi x dx\\ \\ &=&\big[-\dfrac{x^2}{2}-\dfrac{x^3}{3}\big]_{-1}^0 +\big[\dfrac{x^2}{2}-\dfrac{x^3}{3}\big]_0^1-0 \hspace{3em}(\sin \pi x \ \ は奇関数)\\ \\ &=&\big(\cfrac{1}{2}-\cfrac{1}{3}\big)+\big(\cfrac{1}{2}-\cfrac{1}{3}\big)\\ \\ &=&\cfrac{1}{3} \end{eqnarray*}
(4)
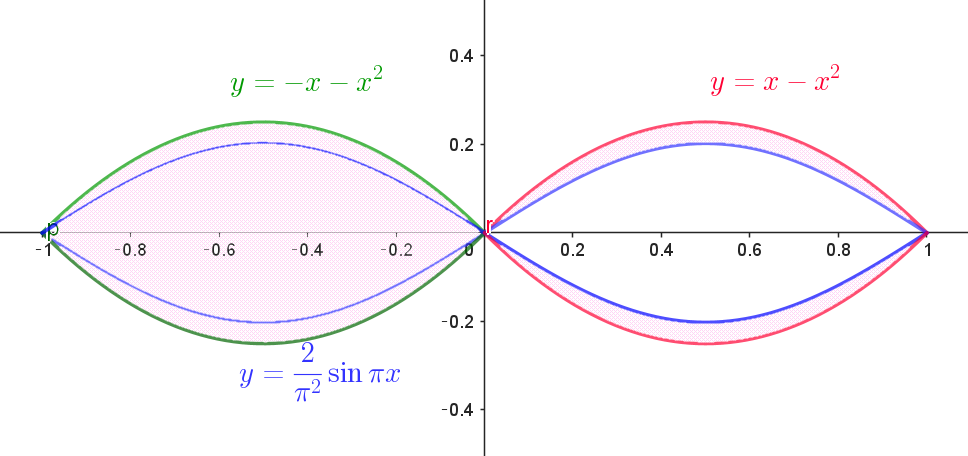
$1回転してできる回転体の体積である。$
\begin{eqnarray*} V &=&\pi\int_{-1}^0(-x-x^2)^2dx+\pi\int_0^1(x-x^2)^2dx\\ \\ & &-\pi\int _0^1\big(\cfrac{2}{\pi^2} \sin \pi x \big)^2dx\\ \\ &=&\pi\int_{-1}^0(x^2+2x^3+x^4)dx+\pi\int_0^1(x^2-2x^3+x^4)dx-\cfrac{4}{\pi^3}\int _0^1\dfrac{1}{2}(1-\cos 2\pi x )dx\\ \\ &=&\pi\big[\dfrac{x^3}{3}+\dfrac{x^4}{2}+\dfrac{x^5}{5}\big]_{-1}^0 +\pi \big[\dfrac{x^3}{3}-\dfrac{x^4}{2}+\dfrac{x^5}{5}\big]_0^1 -\cfrac{2}{\pi^3}\big[x-\dfrac{1}{2\pi}\sin 2\pi x \big]_0^1\\ \\ &=&-\pi\big(-\dfrac{1}{3}+\dfrac{1}{2}-\dfrac{1}{5}\big) +\pi \big(\dfrac{1}{3}-\dfrac{1}{2}+\dfrac{1}{5}\big)-\cfrac{2}{\pi^3} \\ \\ &=&\cfrac{\pi}{15}-\cfrac{2}{\pi ^3} \end{eqnarray*}
メインメニュー に戻る