静岡大学(理系) 2024年 問題2
$A,\ B\ の \ 2\ 名で将棋の対局を行う。対局は必ず勝敗がつくとし、A\ は確率 \ p\ で勝利し、B\ は確率 \ 1-p\ で$
$勝利する。ただし、 0 \leqq p \leqq 1 \ \ とする。対局を複数局行い、先に \ 4\ 局勝利したものを優勝とする。$
$このとき、次の問いに答えよ。$
$(1)\ \ 4\ 局目で \ A,\ B\ が勝利する確率をそれぞれ \ p\ を用いて表せ。$
$(2)\ \ 5\ 局目で優勝者が決まる確率を \ p\ を用いて表せ。$
$(3)\ \ 5\ 局目で優勝者が決まる確率が最大になる \ p\ を求めよ。$
$(4)\ \ (3)で求めた \ p\ に対して、5\ 局目で優勝者が決まる確率を求めよ。$
(1)
$先に \ 4\ 局勝利したものが優勝だから \ 4\ 局目で \ A,\ B\ がそれぞれ優勝するのは$
$4\ 局続けて\ A,\ B\ が勝利する場合である。$
$A\ が優勝する確率は \ \ p^4 ,\quad B\ が優勝する確率は \ \ (1-p)^4$
(2)
$5\ 局目で \ A\ が優勝するのは$
$4\ 局までに \ 3\ 勝 \ 1\ 敗で、5\ 局目に勝利する場合だから \quad {}_4C_3 p^3(1-p) \times p=4p^4(1-p)$
$5\ 局目で \ B\ が優勝するのは$
$4\ 局までに \ 3\ 勝 \ 1\ 敗で、5\ 局目に勝利する場合だから \quad {}_4C_3 (1-p)^3 p \times (1-p)=4p(1-p)^4$
$よって5\ 局目で優勝者が決まる確率 \ P\ は$
\begin{eqnarray*} P &=&4p^4(1-p) + 4p(1-p)^4\\ \\ &=&4\big\{(p^4-p^5)+(p-4p^2+6p^3-4p^4+p^5)\big\}\\ \\ &=&-4(3p^4-6p^3+4p^2-p) \end{eqnarray*}
(3)
$f(p)=-4(3p^4-6p^3+4p^2-p) \quad とおくと$
\begin{eqnarray*} f'(p) &=&-4(12p^3-18p^2+8p-1)\\ \\ &=&-4(p-\dfrac{1}{2})(12p^2-12p+2)\\ \\ &=&-4(2p-1)(6p^2-6p+1) \end{eqnarray*} $f'(p)=0 \ \ より \ \ p=\cfrac{1}{2},\quad \cfrac{3 \pm \sqrt{3}}{6}$
$0 < \cfrac{3-\sqrt{3}}{6} < \cfrac{1}{2} < \cfrac{3+\sqrt{3}}{6} < 1 \quad に注意して$
\[ \begin{array}{c||c|c|c|c|c} p& 0 & \cdots & \dfrac{3-\sqrt{3}}{6} & \cdots & \dfrac{1}{2} & \cdots & \dfrac{3+\sqrt{3}}{6} & \cdots & 1\\ \hline f'(p)& & + & 0 & - & 0 & + & 0 & - & \\ \hline f(p)& 0 & \nearrow & 極大 & \searrow & 極小 & \nearrow & 極大 & \searrow & 0\\ \end{array} \]
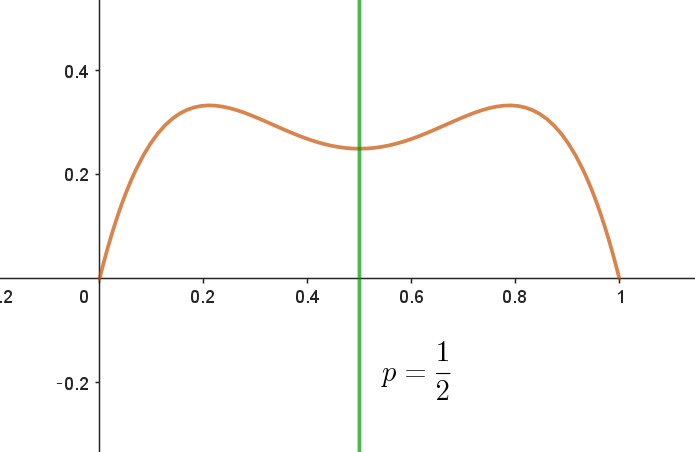
$ここで \quad f(p)=4p^4(1-p) + 4p(1-p)^4 \ \ のグラフは$
$p=\cfrac{1}{2}\ \ で線対称であることを示す。$
$点(p,\ 0)\ の直線 \ \ p=\cfrac{1}{2}\ \ における対称点を \ (p^*,\ 0)\ とすると$
$\cfrac{p+p^*}{2}=\cfrac{1}{2} \quad より \quad p^*=1-p$
$f(p^*)=f(1-p)=4(1-p)^4 p + 4(1-p)p^4=f(p)$
$よって \quad f(p)\ のグラフは \ \ p=\cfrac{1}{2}\ \ で線対称である。$
$とくに \quad p=\cfrac{3-\sqrt{3}}{6} \ \ と \ \ p^*=\cfrac{3+\sqrt{3}}{6}\quad について$
$\cfrac{1}{2}\big(\cfrac{3-\sqrt{3}}{6}+\cfrac{3+\sqrt{3}}{6}\big)=\cfrac{1}{2} \quad だから \quad p=\cfrac{1}{2} \ \ に関して線対称である。$
$したがって 5\ 局目で優勝者が決まる確率が最大になる \ p\ は \quad p=\cfrac{3 \pm\sqrt{3}}{6}$
(4)
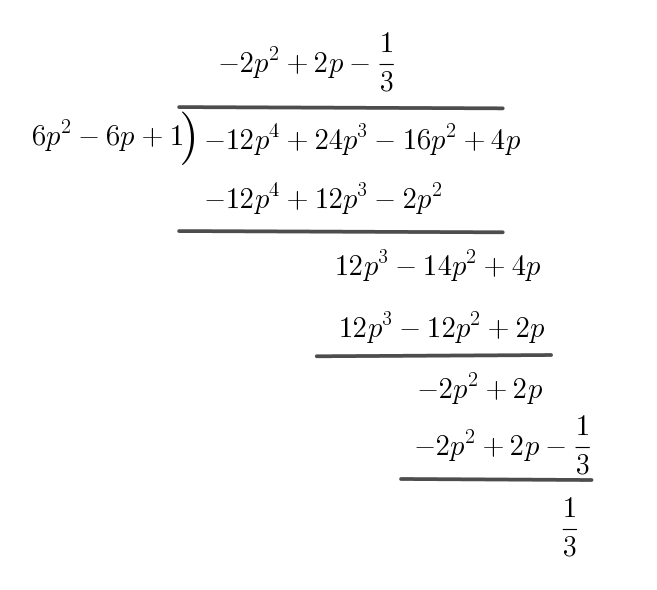
$商と余りを求めると$
$f(p)=(6p^2-6p+1)\big(-2p^2+2p-\dfrac{1}{3}\big)+\cfrac{1}{3}$
$よって \quad f(\dfrac{3 \pm \sqrt{3}}{6})=\cfrac{1}{3}$
$ゆえに \quad p=\dfrac{3 \pm \sqrt{3}}{6} \quad に対して、5\ 局目で優勝者が決まる確率は \quad \cfrac{1}{3}$
メインメニュー に戻る