静岡大学(理系) 2024年 問題1
$座標平面上の直線 \ \ y=\dfrac{1}{\sqrt{3}} x \ \ を \ \ell \ とする。\ell \ 上に中心があり \ x\ 軸の正の部分と接する半径 \ 1\ の円を \ O_1$
$とする。正の整数 \ n\ に対して、O_{n+1}\ を、\ell \ 上に中心があり \ O_n \ と \ x\ 軸の両方に接する円のうち半径が$
$O_n \ より小さい円とする。各円 \ O_n \ の中心の座標を \ (x_n,\ y_n)\ とし、3点\ (x_n,\ y_n),\ (x_{n+1},\ y_{n+1}),\ (x_n,\ y_{n+1})$
$を頂点とする三角形の面積を \ S_n \ とする。このとき、次の問いに答えよ。$
$(1)\ \ y_2 \ を求めよ。$
$(2)\ \ y_n \ を \ n\ の式で表せ。$
$(3)\ \ S_n \ を \ n\ の式で表せ。$
$(4)\ \ S_m > 10^{-5} を満たす最大の正の整数 \ m\ を求めよ。ただし、必要であれば次の不等式$
$\qquad 0.30 < \log_{10} 2 < 0.31, \quad 0.47 < \log _{10} 3 < 0.48 \ \ を用いてよい。$
(1)
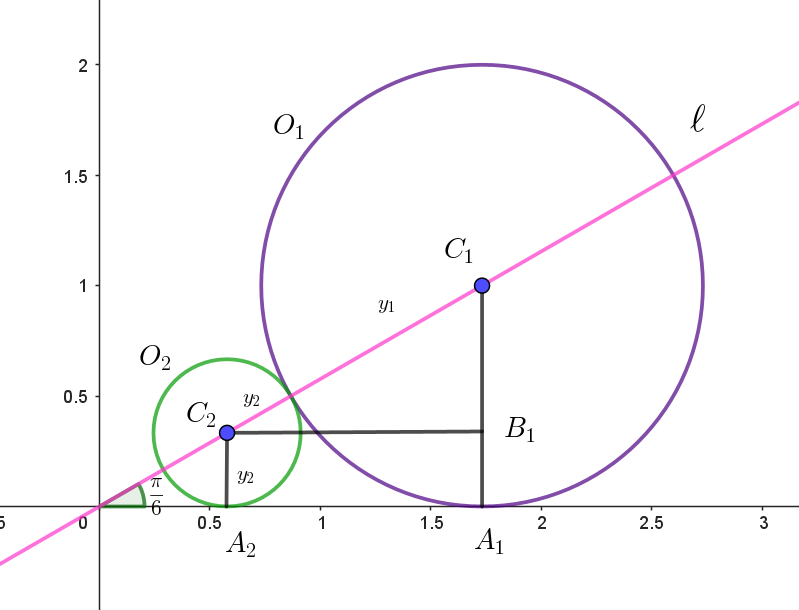
$直線 \ \ell : y=\dfrac{1}{\sqrt{3}} x \ \ 上に中心があるから$
$y_1=\dfrac{1}{\sqrt{3}} x_1 \quad より \quad x_1=\sqrt{3}$
$よって \quad C_1(\sqrt{3},\ 1)$
$円 \ O_2\ は \ x\ 軸に接するから\ \ 半径は \ \ y_2$
$円 \ O_2\ は円 \ O_1\ にも接するから \quad C_1C_2=1+y_2$
$\triangle C_1C_2B_1 \quad において \quad \cfrac{C_1B_1}{C_1C_2}=\sin \dfrac{\pi}{6}$
$\cfrac{1-y_2}{1+y_2}=\cfrac{1}{2} \qquad \therefore \ \ y_2=\cfrac{1}{3}$
$y_2=\dfrac{1}{\sqrt{3}} x_2 \quad より \quad x_2=\cfrac{\sqrt{3}}{3}$
$よって \quad C_2(\dfrac{\sqrt{3}}{3},\ \dfrac{1}{3})$
(2)
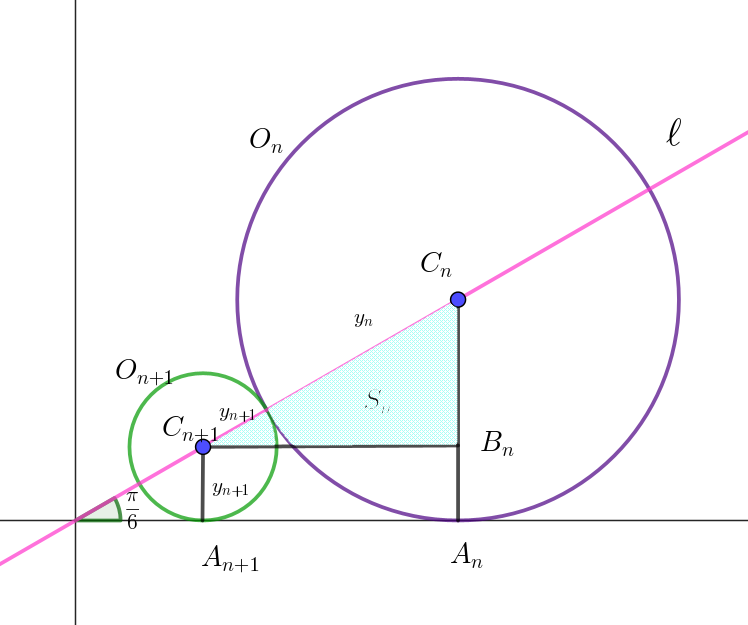
$円\ O_{n+1}\ は \ x\ 軸に接するから \ \ 半径=A_{n+1}C_{n+1}=y_{n+1}$
$円 \ O_{n+1}\ は円 \ O_n\ にも接するから \ \ C_{n+1}C_n=y_n+ y_{n+1}$
$\triangle C_nC_{n+1}B_n \ \ において \quad \cfrac{C_nB_n}{C_nC_{n+1}}=\sin \dfrac{\pi}{6}$
$\cfrac{y_n-y_{n+1}}{y_n + y_{n+1}}=\cfrac{1}{2} $
$y_{n+1}=\cfrac{1}{3}y_n$
$y_n=y_1\big(\dfrac{1}{3}\big)^{n-1}=\big(\dfrac{1}{3}\big)^{n-1}$
(3)
$3\ 点\ (x_n,\ y_n),\ (x_{n+1},\ y_{n+1}),\ (x_n,\ y_{n+1})\ を頂点とする三角形は右図の直角三角形 \ C_nC_{n+1}B_n \ である。$
$直線 \ \ell \ の傾き=\cfrac{y_n-y_{n+1}}{x_n-x_{n+1}}=\cfrac{1}{\sqrt{3}}\ \ より \quad x_n-x_{n+1} =\sqrt{3}(y_n-y_{n+1})$
\begin{eqnarray*} S_n &=&\cfrac{1}{2} \times B_nA_{n+1} \times C_nB_n\\ \\ &=&\cfrac{1}{2}(x_n-x_{n+1})(y_n-y_{n+1})\\ \\ &=&\cfrac{\sqrt{3}}{2}(y_n-y_{n+1})^2\\ \\ &=&\cfrac{\sqrt{3}}{2}(y_n-\dfrac{1}{3}y_n)^2\\ \\ &=&\cfrac{2\sqrt{3}}{9}y_n^2\\ \\ &=&\cfrac{2\sqrt{3}}{9} \times \big(\dfrac{1}{9}\big)^{n-1}\\ \\ &=&\cfrac{2\sqrt{3}}{9^n} \end{eqnarray*}
(4)
$S_m > 10^{-5} \quad より$
$\cfrac{2\sqrt{3}}{9^m} > 10^{-5}$
$\cfrac{1}{9^m} > \cfrac{1}{2\sqrt{3} \times 10^5}$
$9^m < 2\sqrt{3} \times 10^5$
$3^{2m} < 2\sqrt{3} \times 10^5$
$両辺の常用対数をとって(底 \ 10\ は省略)$
$2m\log 3 < 5+\log 2 +\cfrac{1}{2}\log 3$
$m < \cfrac{10+2\log 2 +\log 3}{4\log 3}= \cfrac{1}{4}+\cfrac{5+\log 2}{2\log 3}$
$0.30 < \log_{10} 2 < 0.31 \quad より \quad 5.30 < 5+\log 2 < 5.31$
$0.47 < \log _{10} 3 < 0.48 \quad より \quad 0.94 < 2\log 3 < 0.96$
$ 0.25+\cfrac{5.30}{0.96} < \cfrac{1}{4}+\cfrac{5+\log 2}{2\log 3}< 0.25+\cfrac{5.31}{0.94}$
$5.77 < \cfrac{1}{4}+\cfrac{5+\log 2}{2\log 3} < 5.90$
$求める最大の正の整数は \quad m=5$
メインメニュー に戻る