信州大学(理系) 2024年 問題5
$原点を\ O\ とする座標平面において、直線 \ \ y=\cfrac{1}{\sqrt{3}}x\ \ の \ x > 0 \ の部分を \ \ell , 直線 \ \ y=-\cfrac{1}{\sqrt{3}}x \ \ の \ x > 0 \ の$
$部分を \ m \ とする。点P\ は \ \ell\ 上を、点Q\ は \ m\ 上を、PQ=2\ \ を満たしながら動くとする。このとき、$
$次の問いに答えよ。$
$(1)\ \ \angle OPQ=t \ \ とするとき、P,\ Q\ の座標を \ t\ を用いて表せ。$
$(2)\ \ 線分 \ PQ\ の中点 \ M\ の軌跡を求め、座標平面上に図示せよ。$
(1)
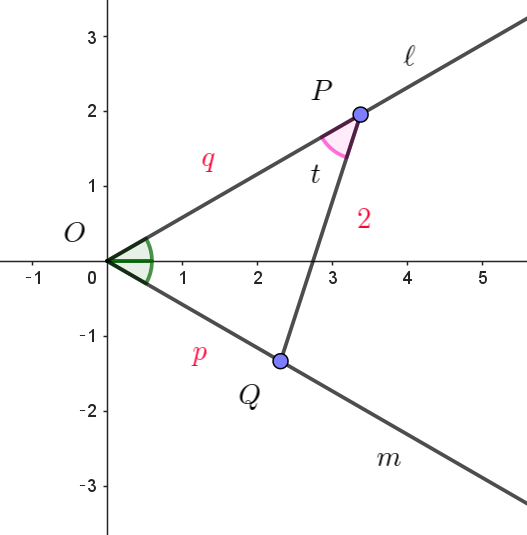
$\triangle OPQ \ \ において \ \ OP=q,\ \ OQ=p \quad とおく。$
$\angle POQ=\cfrac{\pi}{6}+\cfrac{\pi}{6}=\cfrac{\pi}{3}$
$\angle OQP=\pi-t-\cfrac{\pi}{3}=\cfrac{2}{3}\pi-t$
$正弦定理を用いて$
$\cfrac{p}{\sin t}=\cfrac{q}{\sin (\dfrac{2}{3}\pi-t)}=\cfrac{2}{\sin \dfrac{\pi}{3}}$
$p=\cfrac{2}{\sin \dfrac{\pi}{3}} \sin t=\cfrac{4}{\sqrt{3}}\sin t$
\begin{eqnarray*}
q
&=&\cfrac{2}{\sin \dfrac{\pi}{3}} \sin (\dfrac{2}{3}\pi-t)\\
\\
&=&\cfrac{4}{\sqrt{3}} \big(\sin \dfrac{2}{3}\pi \cos t - \cos \dfrac{2}{3}\pi \sin t\big)\\
\\
&=&\cfrac{4}{\sqrt{3}} \big(\cfrac{\sqrt{3}}{2}\cos t + \cfrac{1}{2} \sin t\big)\\
\\
&=&2\cos t+ \cfrac{2}{\sqrt{3}} \sin t
\end{eqnarray*}
$点Pについて$
$\quad x=q\cos \dfrac{\pi}{6}=\big(2\cos t+ \cfrac{2}{\sqrt{3}} \sin t \big) \times \cfrac{\sqrt{3}}{2}=\sqrt{3}\cos t+\sin t$
$\quad y=q\sin \dfrac{\pi}{6}=\big(2\cos t+ \cfrac{2}{\sqrt{3}} \sin t \big) \times \cfrac{1}{2}=\cos t+ \dfrac{1}{\sqrt{3}}\sin t$
$\therefore \ \ P(\sqrt{3}\cos t+\sin t , \ \cos t+ \dfrac{1}{\sqrt{3}}\sin t )$
$点Qについて$
$\quad x=p\cos \dfrac{\pi}{6}= \cfrac{4}{\sqrt{3}} \sin t \times \cfrac{\sqrt{3}}{2}=2\sin t$
$\quad y=p\sin \dfrac{\pi}{6}= \cfrac{4}{\sqrt{3}} \sin t \times \cfrac{1}{2} = \dfrac{2}{\sqrt{3}}\sin t$
$\therefore \ \ Q(2\sin t , \ - \cfrac{2}{\sqrt{3}}\sin t )$
$ただし、\angle OPQ= t > 0,\quad \angle OQP=\cfrac{2}{3}\pi-t > 0 \quad より \quad 0 < t < \cfrac{2}{3}\pi$
(2)
$M(x,\ y)\ \ とおくと$
\begin{eqnarray*} x &=&\cfrac{1}{2}\big((\sqrt{3}\cos t+\sin t)+2\sin t\big)\\ \\ &=&\cfrac{1}{2}(3\sin t+\sqrt{3}\cos t)\\ \\ &=&\cfrac{\sqrt{3}}{2}(\sqrt{3}\sin t+\cos t)\\ \\ &=&\sqrt{3}\sin (t+ \dfrac{\pi}{6})\\ \end{eqnarray*}
\begin{eqnarray*} y &=&\cfrac{1}{2}\big((\cos t + \dfrac{1}{\sqrt{3}}\sin t )- \cfrac{2}{\sqrt{3}}\sin t \big)\\ \\ &=&\cfrac{1}{2}(\cos t - \cfrac{1}{\sqrt{3}}\sin t )\\ \\ &=&\cfrac{1}{2\sqrt{3}}(\sqrt{3}\cos t- \sin t)\\ \\ &=&\cfrac{1}{\sqrt{3}}\cos (t + \dfrac{\pi}{6})\\ \end{eqnarray*}
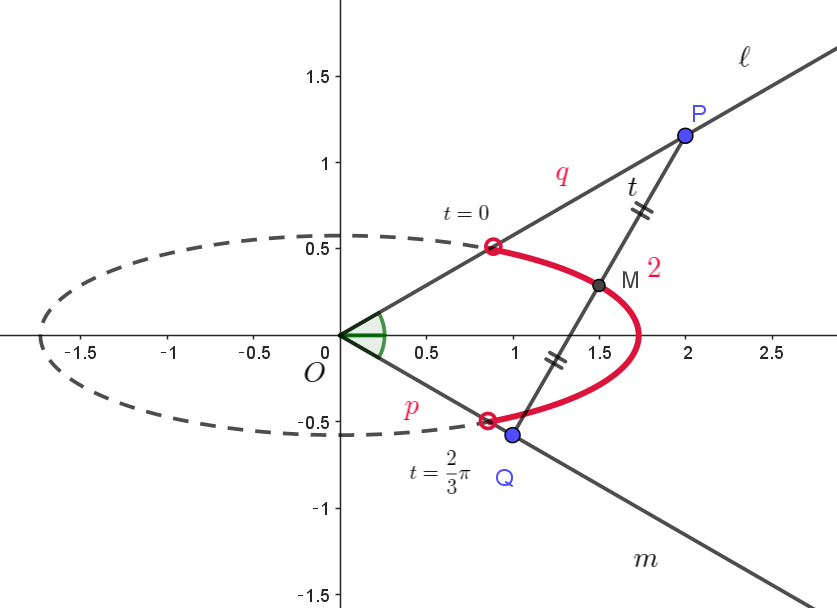
$\big(\cfrac{x}{\sqrt{3}}\big)^2+ (\sqrt{3}y)^2=\sin ^2(t+ \dfrac{\pi}{6}) + \cos ^2 (t+ \dfrac{\pi}{6})=1$
$したがって、 線分 \ PQ\ の中点 \ M\ の軌跡は$
$楕円 \quad \cfrac{x^2}{3} + 3y^2=1$
$ただし、0 < t < \cfrac{2}{3}\pi \quad より$
$t=0 \ \ のとき \quad M(\dfrac{\sqrt{3}}{2},\ \dfrac{1}{2})$
$t=\cfrac{2}{3}\pi \ \ のとき \quad M(\dfrac{\sqrt{3}}{2},\ -\dfrac{1}{2})$
$グラフは右図で、この \ 2\ 点を除いた、\cfrac{\sqrt{3}}{2} < x \leqq \sqrt{3} \quad の部分の赤い部分である。$
メインメニュー に戻る