信州大学(理系) 2024年 問題3
$平面上の2つのベクトル \ \ \vec{a},\ \ \vec{b} \ \ は、|\vec{a}|=2,\ \ |\vec{b}|=1,\ および \ \ \vec{a} \cdot \vec{b}=1\ \ を満たすとする。k\ を定数とし、$
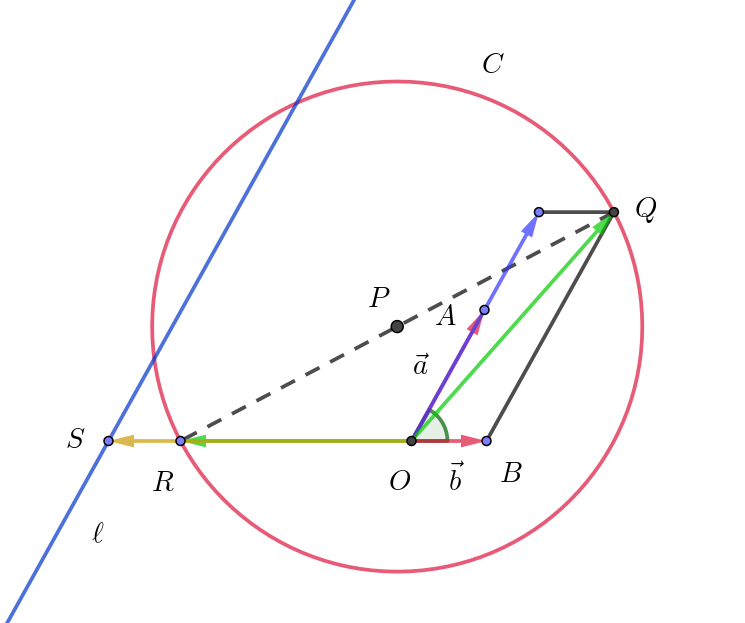
$2\ 点Q(2k\vec{a}+\vec{b}),\ \ R(-3\vec{b})\ \ を直径の両端とする円を \ C,\ \ 点S(-4\vec{b})\ \ を通り、\vec{a}\ \ に平行な直線を \ \ell \ とする。$
$このとき、次の問いに答えよ。$
$(1)\ \ 円 \ C\ の半径 \ r\ を \ k\ を用いて表せ。$
$(2)\ \ 直線 \ \ell \ が円 \ C\ と共有点をもつとき、k\ のとり得る値の範囲を求めよ。$
(1)
\begin{eqnarray*} \vec{RQ} &=&\vec{OQ}-\vec{OR}\\ \\ &=&(2k\vec{a}+\vec{b})-(-3\vec{b})\\ \\ &=&2k\vec{a}+4\vec{b}\\ \end{eqnarray*}
\begin{eqnarray*}
|\vec{RQ}|^2
&=&|2k\vec{a}+4\vec{b}|^2\\
\\
&=&4k^2|\vec{a}|^2+16|\vec{b}|^2+16k\vec{a} \cdot \vec{b}\\
\\
&=&4k^2 \times 2^2 +16 \times 1^2 +16k \times 1\\
\\
&=&16(k^2+k+1)
\end{eqnarray*}
$|\vec{RQ}|=4\sqrt{k^2+k+1}$
$\therefore \ \ r=\cfrac{1}{2}RQ=2\sqrt{k^2+k+1}$
(2)
$円 \ C\ の中心を \ P\ とすると$
\begin{eqnarray*} \vec{OP} &=&\cfrac{1}{2}(\vec{OQ}+\vec{OR})\\ \\ &=&\cfrac{1}{2}(2k\vec{a}+\vec{b})+(-3\vec{b})\\ \\ &=&k\vec{a}-\vec{b}\\ \end{eqnarray*} $(1)より円 \ C\ の半径は \quad r=\cfrac{1}{2}RQ=2\sqrt{k^2+k+1} \quad だから$
$円 \ C\ の方程式は \quad |\vec{x}-(k\vec{a}-\vec{b})|=2\sqrt{k^2+k+1} \hspace{17em}①$
$点S(-4\vec{b})\ \ を通り、\vec{a}\ \ に平行な直線 \ \ell の方程式は \quad \vec{x}=-4\vec{b}+m\vec{a}\ \ (m\ は実数) \hspace{5em}②$
$直線 \ \ell \ と円 \ C\ の共有点は②を①に代入して$
$|-4\vec{b}+m\vec{a} -k\vec{a}+\vec{b})|=2\sqrt{k^2+k+1} $
$|(m-k)\vec{a}-3\vec{b}|=2\sqrt{k^2+k+1} $
$両辺平方して$
$(m-k)^2|\vec{a}|^2 +9|\vec{b}|^2-6(m-k)\vec{a}\cdot \vec{b}=4(k^2+k+1)$
$4(m-k)^2 +9 -6(m-k)=4(k^2+k+1)$
$4m^2-2(4k+3)m+2k+5=0$
$m\ は実数だから$
$\cfrac{D}{4}=(4k+3)^2-4(2k+5) \geqq 0$
$16k^2+16k-11 \geqq 0$
$16k^2+16k-11 0\ \ の解は \quad k=\cfrac{-8 \pm \sqrt{64+16 \times 11}}{16}=\cfrac{-2 \pm \sqrt{15}}{4} \quad だから$
$直線 \ \ell \ と円 \ C\ が共有点をもつ\ k\ の値の範囲は$
$ \quad k \geqq \cfrac{-2 + \sqrt{15}}{4} ,\quad k \leqq \cfrac{-2 - \sqrt{15}}{4}$
メインメニュー に戻る