信州大学(理系) 2024年 問題1
$座標平面上の放物線 \ C:y=x^2\ 上に異なる \ 2\ つの動点 \ P(p,\ p^2),\ Q(q,\ q^2)\ をとる。ただし、実数 \ p,\ q\ は$
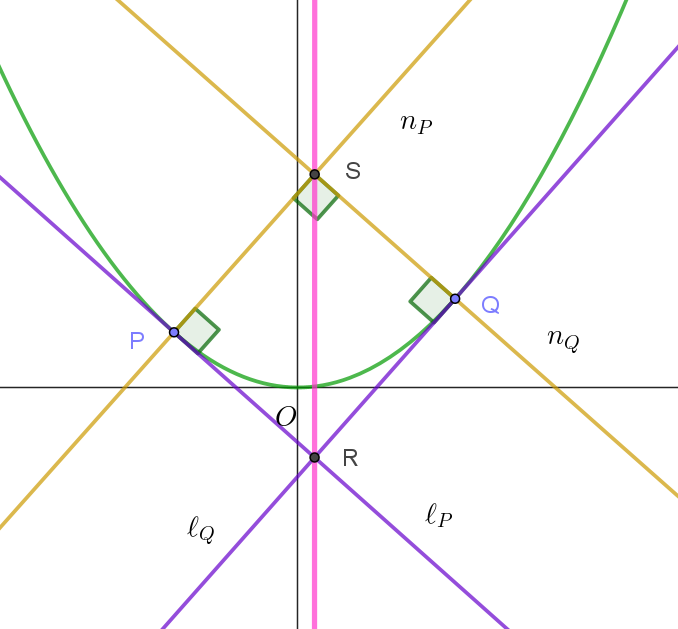
$p < q ,\ \ pq \ne 0\ を満たすとする。P\ における \ C\ の接線を \ \ell_P,\ Pを通り \ \ell_P \ に垂直な直線を \ n_p,\ Q\ における$
$ \ C\ の接線を \ \ell_Q,Q\ を通り \ \ell_Q \ に垂直な直線を \ n_Q \ とする。また、\ell_p \ と \ \ell_Q \ の交点を \ R,n_p\ と \ n_Q\ の交点を$
$S\ とし、\angle PSQ=90°であるとする。このとき、次の問いに答えよ。$
$(1)\ \ 直線\ RS\ と \ y\ 軸が平行であることを示せ。$
$(2)\ \ 四角形 \ PRQS\ の面積 \ T\ を \ q\ を用いて表せ。また、T\ の最小値を求めよ。$
(1)
$\ell_P \ \ は \ \ y=2p(x-p)+ p^2=2px-p^2$
$n_P \ \ は \ \ y=-\cfrac{1}{2p}(x-p)+ p^2=-\cfrac{1}{2p}x+p^2+\cfrac{1}{2}$
$\ell_Q \ \ は \ \ y=2q(x-q)+ q^2=2qx-q^2$
$n_Q \ \ は \ \ y=-\cfrac{1}{2q}(x-q)+ q^2=-\cfrac{1}{2q}x+q^2+\cfrac{1}{2}$
$\angle PSQ=90°\quad より \quad n_P \perp n_Q$
$\big(-\cfrac{1}{2p}\big) \times \big(-\cfrac{1}{2q}\big) =-1$
$\therefore \ \ pq=-\cfrac{1}{4}$
$点R\ の \ x\ 座標は \ \ \ell_P \ \ と \ \ \ell_Q \ \ の交点だから$
$\quad 2px-p^2=2qx-q^2 \quad を解いて$
$\quad 2(p-q)x=p^2-q^2 \quad p \ne q \quad だから \quad x=\cfrac{p+q}{2}$
$点S\ の \ x\ 座標は \ \ n_P\ \ と \ \ n_Q \ \ の交点だから$
$\quad -\cfrac{1}{2p}x+p^2+\cfrac{1}{2}=-\cfrac{1}{2q}x+q^2+\cfrac{1}{2}$
$\quad \cfrac{1}{2}\big(\cfrac{1}{p}-\cfrac{1}{q}\big)x=p^2-q^2$
$\quad -\cfrac{p-q}{2pq}x=p^2-q^2 \quad p \ne q \quad だから$
$\quad x=-2pq(p+q)=-2 \times (-\cfrac{1}{4}) (p+q)=\cfrac{p+q}{2}$
$点R \ の \ x\ 座標と点Q\ の \ x\ 座標が一致するから直線\ RS\ と \ y\ 軸は平行である。$
(2)
$点R\ の \ y\ 座標は$
$\quad y=2p \times \cfrac{p+q}{2} -p^2=pq=-\cfrac{1}{4}$
$点S\ の \ y\ 座標は$
\begin{eqnarray*} \quad y &=&-\cfrac{1}{2q} \times \cfrac{p+q}{2} +q^2+\cfrac{1}{2}\\ \\ &=&-\cfrac{p}{4q} -\cfrac{1}{4} +q^2+\cfrac{1}{2}\\ \\ &=&\cfrac{1}{16q^2} +q^2+\cfrac{1}{4}\\ \end{eqnarray*}
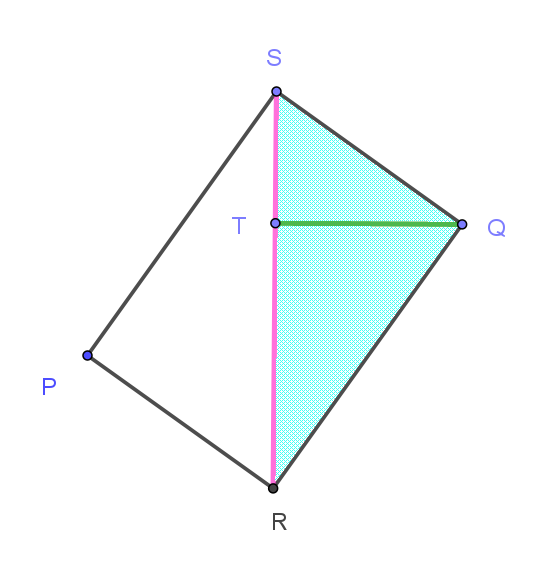
$四角形PRQS \ は \ 3\ つの内角が \ 90°\ だから長方形である。$
$点Q\ から対角線 \ RS\ に下ろした垂線を \ QT\ とする。$
\begin{eqnarray*}
T
&=&2\triangle QRS\\
\\
&=&RS \times QT\\
\\
&=&\big\{\big(\cfrac{1}{16q^2} +q^2+\cfrac{1}{4}\big\}-\big(-\cfrac{1}{4}\big)\big\} \times \big(q-\cfrac{p+q}{2}\big)\\
\\
&=&\big\{\big(\cfrac{1}{16q^2} +q^2+\cfrac{1}{4}\big\}-\big(-\cfrac{1}{4}\big)\big\} \times \big(q-\cfrac{p+q}{2}\big)\\
\\
&=&\big(\cfrac{1}{16q^2} +q^2+\cfrac{1}{2} \big) \times \cfrac{q-p}{2}\\
\\
&=&\cfrac{1}{2}\big(q + \cfrac{1}{4q} \big)^2 \big(q + \cfrac{1}{4q}\big)\\
\\
&=&\cfrac{1}{2}\big(q + \cfrac{1}{4q} \big)^3
\end{eqnarray*}
$ここで、pq=-\cfrac{1}{4} , \quad p < q \quad だから \quad q > 0$
$相加・相乗平均の不等式より \quad q + \cfrac{1}{4q} \geqq 2\sqrt{q \times \cfrac{1}{4q}}=1$
$\quad ただし等号は \quad q=\cfrac{1}{4q} \quad より \quad q^2=\cfrac{1}{4} \quad q=\cfrac{1}{2} \quad のとき$
$したがって \quad q=\cfrac{1}{2} \quad のとき、T\ は最小値 \quad T=\cfrac{1}{2}\quad をとる。$
$(補充)$
$q=\cfrac{1}{2}\quad のとき \quad p=-\cfrac{1}{2} \quad だから$
$P(-\cfrac{1}{2},\ \cfrac{1}{4}),\quad Q(\cfrac{1}{2},\ \cfrac{1}{4}),\quad R(0,\ -\cfrac{1}{4}),\quad S(0,\quad \cfrac{3}{4})\quad となり$
$PQ \ は \ x\ 軸に平行、RS\ は \ y\ 軸だから \quad PQ \perp RS$
$したがって\quad 四角形PRQS \ \ は正方形となる。$
メインメニュー に戻る