三平方の定理
1 はじめに
$「直角三角形で、直角に対する辺上の正方形は直角にはさまれている辺上の正方形の和と等しい。」$
$という超有名な三平方の定理(ピタゴラスの定理)を初めて教わったのは中学校3年のときである。$
$必死になって理解しようとしたのを覚えている。$
$最近、といってももう何年も前であるが、必要があって中学校の教科書を見てびっくりした。$
$三平方の定理の証明が全く変わっていたのである。いつからそうなったのかわからないが、$
$その簡単さにショックであった。$
$あのときこの証明方法が教科書にのっていたならば理解するのに苦労しなかっただろう。$
$そこで、私が苦労した証明方法と、今の証明方法とを比べてみたい。$
2 昔の証明方法(ユークリッドの原論風のやりかた)
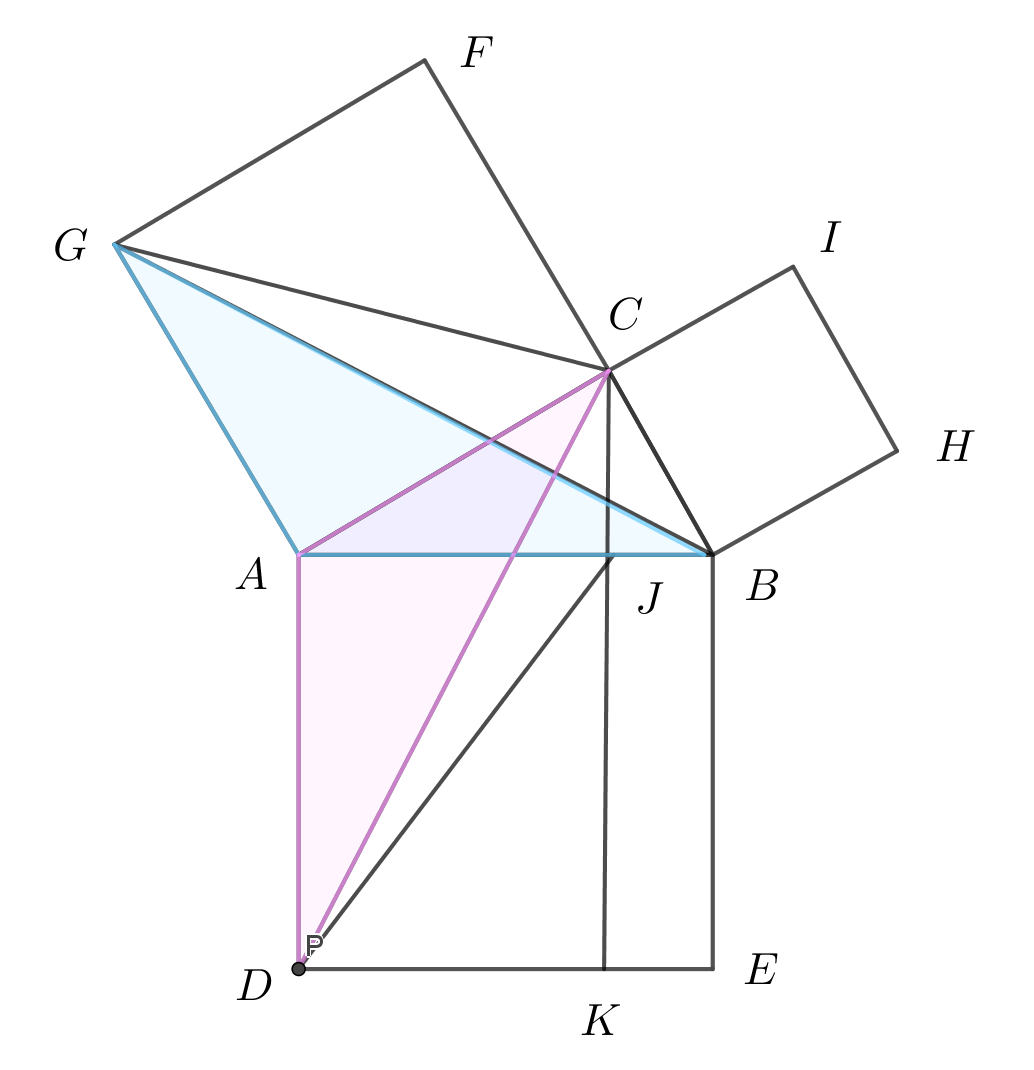
$それぞれ正方形を立てる。点Cから辺ABに垂線CJを下ろし、$
$辺DEとの交点をKとする。$
(i)$\ △ADCと△ABGにおいて$
$\qquad AD=AB $
$\qquad AC=AG $
$\qquad ∠CAD=∠CAB+∠BAD=∠CAB+90°$
$\qquad ∠GAB=∠GAC+∠CAB=90°+∠CAB$
$\quad よって ∠CAD=∠GAB $
$\quad 2辺とその間の角が等しいので △ADC \equiv △ABG \hspace{5em}(1)$

$\qquad 底辺ADは共通$
$\qquad AD \ //\ CJ だから 高さはともに \ AJ$
$\quad よって △ADC=△ADJ \hspace{15em}(2)$
(iii)$\ △GABと△GACにおいて$
$\qquad 底辺GAは共通$
$\qquad GA \ //\ CB だから 高さはともに \ AC$
$\quad よって △GAB=△GAC \hspace{15em}(3)$
$(1),(2),(3)より △ADJ=△ACG \hspace{12em}(4)$
また
$\qquad 長方形ADKJ=2△ADJ \hspace{15em}(5)$
$\qquad 正方形ACFG=2△ACG \hspace{15em}(6)$
$(4),(5),(6)より 長方形ADKJ=正方形ACFG \hspace{8em}(7)$
$同様にして 長方形BEKJ=正方形BHIC \hspace{10em}(8)$
$正方形ADEB= 長方形ADKJ + 長方形BEKJ だから \hspace{4em}(9)$
$(7),(8),(9)より 正方形ADBE = 正方形ACFG + 正方形BHIC$
$すなわち$
$直角三角形で、直角に対する辺上の正方形は直角にはさまれている辺上の正方形の和と等しい。$
$当時の教科書の文言までは覚えていないが、おそらくこのような内容だったと思われる。$
2 今の証明方法

$AB=DE=FG=HC となるように4点B,E,G,Cをとる。$
$2辺とその間の角(直角)が等しいので$
$\quad △ABC \equiv △DEB \equiv △FGE \equiv △HCG $
$よって CB=BE=EG=GC$
\begin{eqnarray*} ∠CBE&=&180°-(∠ABC+∠EBD)\\ &=&180°-(∠ABC+∠BCA)\\ &=&180°-90°\\ &=&90°\\ \end{eqnarray*} $したがって、四角形BEGCは正方形となる。$
$AB=a,\ CA=b,\ BC=c とすると$
$正方形BEGC=正方形ADFH-4 \times △ABC だから$
$\quad c^2=(a+b)^2-4 \times \cfrac{1}{2}ab=(a^2+2ab+b^2)-2ab$
$\quad \therefore c^2=a^2+b^2$
$確かに、この方法は簡単で分かりやすい。そして何より教える方にとっては時間がかからない。$
$今の時代、この時間がかからないことが一番重要なポイントなのです。$
$学校が週5日制になり、様々な教科外活動が入ってきてますます既存教科の学習時間が減る中で、$
$なるべく簡単で時間がかからない指導法が求められているわけです。$
$図形(幾何)の性質を理解するのに、なにも図形だけでやる必要はない。$
$三平方の定理ぐらいは計算を取り入れてもいいだろうとの考えでしょう。$
$確かに、高校になると図形の性質を調べるのに、座標を使ったり、ベクトルや複素数を使ったり$
$します。(解析幾何といいます)。$
$一方、いくら時間がないとはいえ、三平方の定理の証明はやはりユークリッド風に三角形の合同$
$と等積変換でやるべきかいなか、という考え方もあるでしょう。$
$ここは、意見が分かれるところです。$
$十分に年を取った今の私の考えは、「三平方の定理」は中学校の図形の学習の総仕上げであるの$
$で、そのとき理解できなくてもいいから、また時間がかかってもいいからやるべきだと思ってい$
$ます。$
$実は、これを言いたいがために、このページを書きました。$
3 計算による別の証明方法
計算で証明してもよいならば多様な方法が知られていますので、そのうちいくつかを示します。
(1)
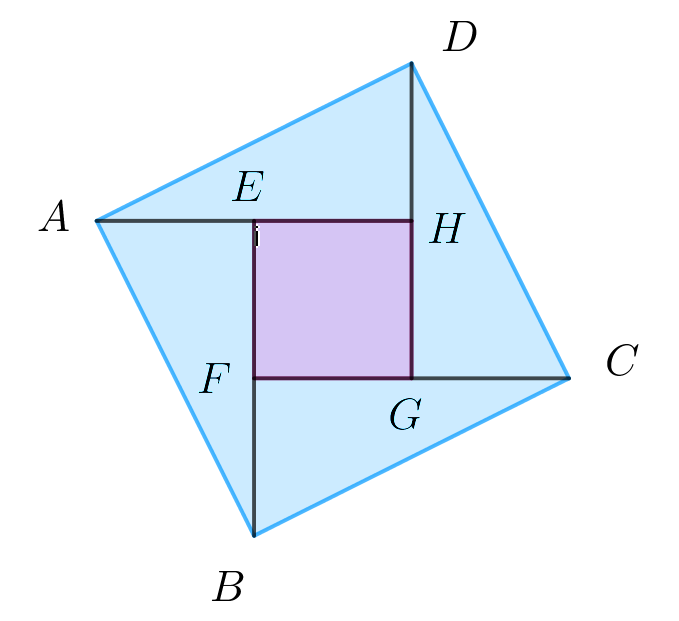
$合同な三角形を右図のように配置する。$
$四角形ABCDは4辺が等しく、$
$∠A=∠DAH+∠BAE=∠ABE+∠BAE=90°$
$よって 四角形ABCDは正方形である。$
$また、 EF=BE-BF=BE-AE=a-b$
$同様にして、四角形EFGHは4辺とも、a-b になるから正方形である。$
$\quad 正方形ABCD=正方形EFGH + 4\times △ABE より$
$\quad c^2=(a-b)^2+4\times \cfrac{1}{2}ab$
$\quad \therefore c^2=a^2+b^2$
(2)

$3点D,\ C,\ B\ が一直線上に並ぶようにおく。$
\begin{eqnarray*} ∠ACE&=&180°-(∠BCA+∠DCE)\\ &=&180°-(∠BCA+∠BAC)\\ &=&180°-90°\\ &=&90°\\ \end{eqnarray*} $よって、△ACEは\ ∠ACE=90°\ の直角二等辺三角形となる。$
$DB \perp ED ,\ DB \perp AB だから ED \ //\ AB となり、四角形ABDEは台形$
$△ACE+ △ABC + △CDE =台形ABDE より$
$\quad \cfrac{1}{2}c^2+2 \times \cfrac{1}{2}ab =\cfrac{1}{2}(a+b)^2$
$\quad c^2+2ab=(a+b)^2$
$\quad \therefore c^2=a^2+b^2$
$この証明は、アメリカ第20代大統領 ガーフィールドによるものと言われています。$
$よくできていますね。$
(3)
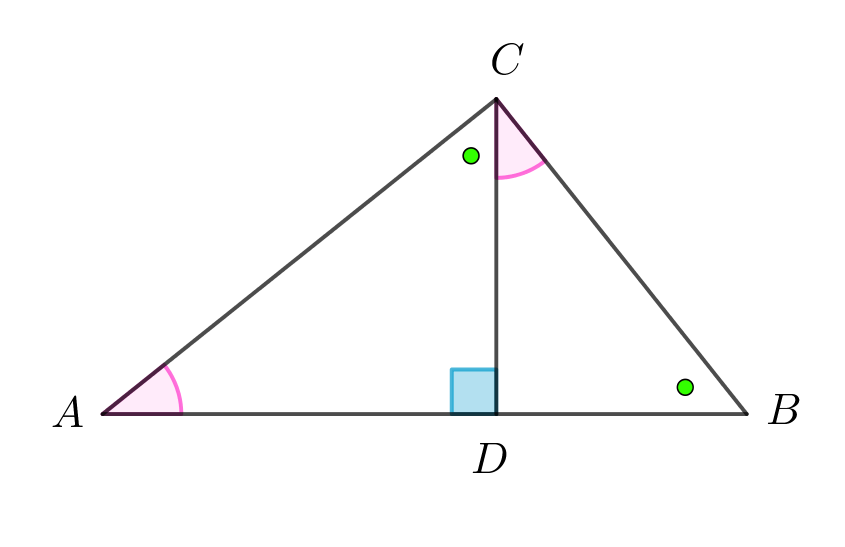
$点Cより、対辺AB\ に垂線を下ろしCDとする。$
$BC=a,\ CA=b,\ AB=c,\ BD=t,\ AD=u \ とおく$
$\quad △ACDで、∠A+∠ACD=90°$
$\quad ∠C=∠BCD+∠ACD=90°$
$よって、∠A=∠BCD$
$\quad ∠ACD=90°-∠A=90°-∠BCD=∠B$
$△ABC \ ∽ \ △ACD だから$
$\quad AB : AC= AC : AD$
$\quad c:b=b:u$
$\quad b^2=cu \hspace{10em}(1)$
$△ABC \ ∽ \ △CBD だから$
$\quad AB : CB= BC : BD$
$\quad c:a=a:t$
$\quad a^2=ct \hspace{10em}(2)$
$(1)+(2) より a^2+b^2=ct+cu=c(t+u)=c^2$
$\quad \therefore c^2=a^2+b^2$
メインメニュー に戻る