埼玉大学(理系) 2024年　問題4


$関数 \ f(x)\ を \ f(x)=\dfrac{1}{3}\sqrt{9-x^2}\ \ (-3 < x < 3) \ \ とし、xy\ 平面上の曲線 \ C\ を \ C:y=f(x)\ \ (-3 < x < 3 )\ \ に$
$より定める。次の問いに答えよ。$
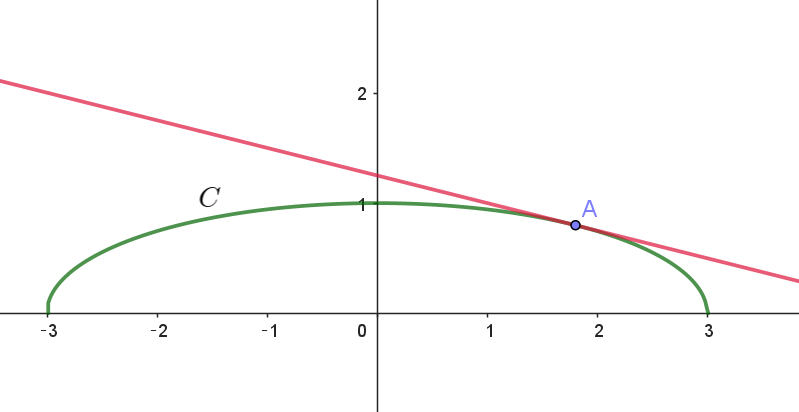
$(1)\ \ C上の点\ (t,\ f(t))\ \ (-3 < t < 3)\ \ における \ C\ の接線の方程式を求めよ。$
$(2)\ \ 実数 \ m\ に対して、C\ の接線であって傾きが \ m\ のものがちょうど \ 1\ 本存在することを示し、その接線$
$\quad の \ y\ 切片を \ m\ を用いて表せ。$
$(3)\ \ 点(2\sqrt{2},\ \sqrt{2})\ を通る \ C\ の接線がちょうど \ 2\ 本存在し、それらが直交することを示せ。$
$(4)\ \ a,\ b\ を \ -3 < a < 3 \ \ および \ \ b \ > 1 \ \ を満たす実数とする。点(a,\ b)\ を通る \ C\ の接線がちょうど \ 2\ 本$
$\quad 存在し、それらが直交するとする。このとき \ \ y=\sqrt{10-a^2}\ \ が成り立つことを示せ。$


(1)

　

$y=\dfrac{1}{3}\sqrt{9-x^2} \quad より \quad (3y)^2=9-x^2$

$x^2+9y^2=9 \qquad \cfrac{x^2}{9}+y^2=1$

$よって 曲線 \ C\ は楕円の上半分である。$

$y=\dfrac{1}{3}\sqrt{9-x^2} \quad より \quad y'=\cfrac{1}{3} \cfrac{-x}{\sqrt{9-x^2}}$

$点\ (t,\ f(t))\ \ (-3 < t < 3)\ \ における \ C\ の接線は$

\begin{eqnarray*} y &=&-\cfrac{t}{3\sqrt{9-t^2}}(x-t)+\cfrac{1}{3}\sqrt{9-t^2}\\ \\ &=&-\cfrac{t}{3\sqrt{9-t^2}}x + \cfrac{t^2}{3\sqrt{9-t^2}} +\cfrac{1}{3}\sqrt{9-t^2}\\ \\ &=&-\cfrac{t}{3\sqrt{9-t^2}}x + \cfrac{9}{3\sqrt{9-t^2}}\\ \end{eqnarray*} $分母を払って$

$3\sqrt{9-t^2}y=-tx+9$

$\cfrac{t}{9}x+\cfrac{\sqrt{9-t^2}}{3}y=1$

$\therefore \ \ \cfrac{t}{9}x+f(t)y=1$


(2)


$傾き \ m\ の接線を \ \ y=mx+n \ \ とおくと曲線 \ C\ との交点は$

$x^2+9y^2=9 \quad に代入して$

$x^2+9(mx+n)^2=9$

$(1+9m^2)x^2+18mnx + 9n^2-9=0$

$接する条件は \ D=0\ \ だから$

$\cfrac{D}{4}=(9mn)^2-(1+9m^2)(9n^2-9)=0$

$9m^2n^2-(1+9m^2)(n^2-1)=0$

$n^2=9m^2+1$

$明らかに \ n > 0\ \ だから \quad n=\sqrt{9m^2+1}$

$よって傾きが \ m\ の接線はちょうど \ 1\ 本存在してそれは \quad y=mx+\sqrt{9m^2+1}$

$y\ 切片は \quad \sqrt{9m^2+1}$


(3)

　

$(2)より 傾き \ m\ の接線は \quad y=mx+\sqrt{9m^2+1}$

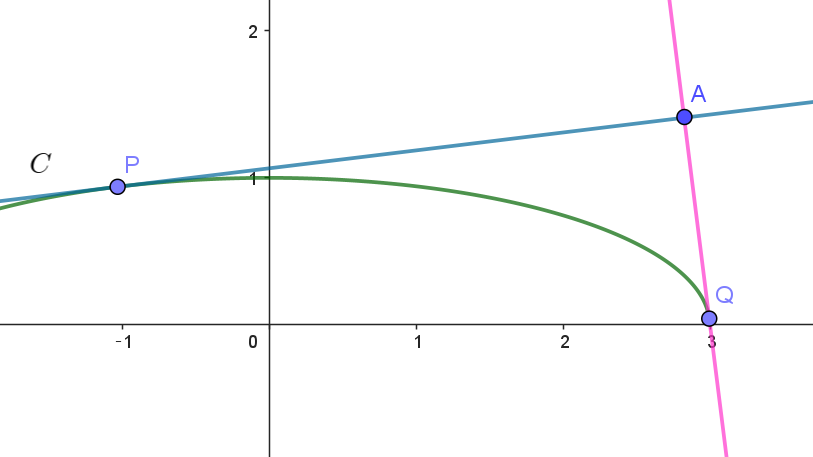
$これが、点A(2\sqrt{2},\ \sqrt{2})\ を通るから$

$\sqrt{2}=2\sqrt{2}m+\sqrt{9m^2+1}$

$\sqrt{2}(1-2m)=\sqrt{9m^2+1}$

$2(1-2m)^2=9m^2+1$

$m^2+8m-1=0$

$m=-4 \pm \sqrt{17}$

$これを \ m_1,\ m_2 \ \ とおくと$

$接線は \ \ y=m_1x+\sqrt{9m_1^2+1}\ \ と \ \ y=m_2x+\sqrt{9m_2^2+1}\ \ のちょうど \ 2\ 本存在する。$

$解と係数の関係より \quad m_1m_2=-1 \quad であるから2\ 本の接線は直交する。$


(4)

　

$(2)より 傾き \ m\ の接線は \quad y=mx+\sqrt{9m^2+1}$

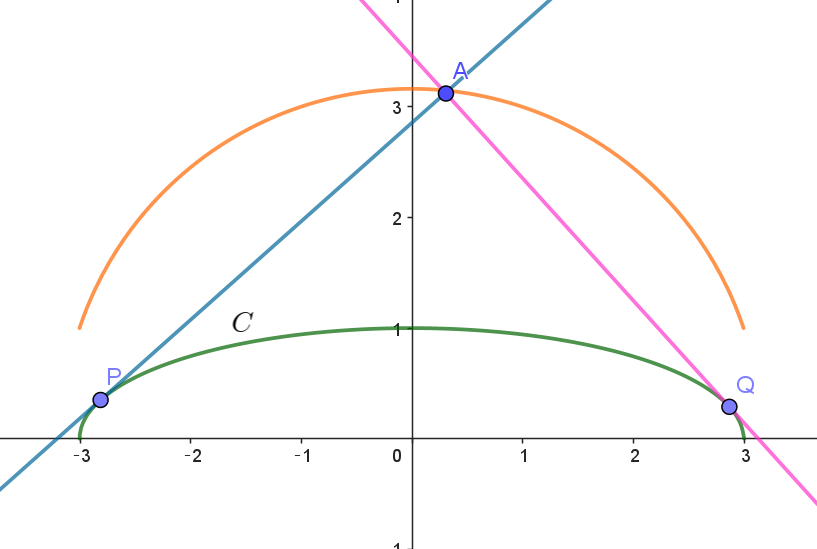
$これが、点A(a,\ b)\ を通るから$

$b=ma+\sqrt{9m^2+1}$

$b-ma=\sqrt{9m^2+1}$

$(b-ma)^2=9m^2+1$

$(a^2-9)m^2-2abm+b^2-1=0$

$\cfrac{D}{4}=a^2b^2-(a^2-9)(b^2-1)=a^2+9(b^2-1)$

$b > 1\ \ だから \ \ D > 0 \ \ となって m\ についてのこの \ 2\ 次方程式は異なる \ 2\ つの実数解をもつ。$

$よって 接線はちょうど \ 2\ 本存在する。この解を \ m_1,\ m_2 \ \ とおくと$

$それらが直交するから \quad m_1m_2=-1$

$解と係数の関係より \quad m_1m_2=\cfrac{b^2-1}{a^2-9}=-1 $

$b^2=10-a^2$

$b > 0\ \ だから \quad b=\sqrt{10-a^2}$


$(注意)$

$(3)は(4)で、a=2\sqrt{2},\ \ b=\sqrt{2} \ \ とおいたものである。$


ページの先頭へ↑



メインメニュー　に戻る