埼玉大学(理系) 2024年　問題3


$\theta \ を \ 0 \leqq \theta \leqq \dfrac{\pi}{2}\ を満たす実数とする。点 \ O\ を原点とする \ xy\ 平面上に点 \ H\big(\dfrac{\sqrt{2}}{2}\cos (\theta + \dfrac{\pi}{4}),\ \dfrac{\sqrt{2}}{2}\sin (\theta + \dfrac{\pi}{4})\big)$
$をとる。H\ を通り、直線 \ OH\ と直交する直線を \ \ell \ とする。また曲線 \ C\ を \ C:y=\sqrt{1-x^2}\ \ (-1 \leqq x \leqq )\ \ に$
$より定め、\ell \ と \ C\ の交点を \ x\ 座標の小さい順に \ P_1,\ P_2\ とする。線分 \ OP_1\ と線分 \ OP_2\ と \ C\ で囲まれた部分$
$を \ x\ 軸の周りに \ 1\ 回転させてできる立体の体積を \ V\ とする。次の問いに答えよ。$
$(1)\ \ \triangle HOP_1,\ \ \triangle HOP_2 \ \ がいずれも直角二等辺三角形であることを示し、\angle HOP_1=\angle HOP_2 =\dfrac{\pi}{4} \ \ である$
$\quad ことを示せ。$
$(2)\ \ P_1,\ \ P_2 \ の 座標を求めよ。$
$(3)\ \ \dfrac{V}{\sin \theta + \cos \theta }\ \ の値は \ \theta \ によらず一定であることを示せ。$
$(4)\ \ \theta \ の値が \ \ 0 \leqq \theta \leqq \dfrac{\pi}{2}\ \ の範囲を動くときの \ V\ の最大値およびそのときの \ \theta \ の値を求めよ。$


(1)

　

$\angle HOP_2=\alpha \quad とおくと$

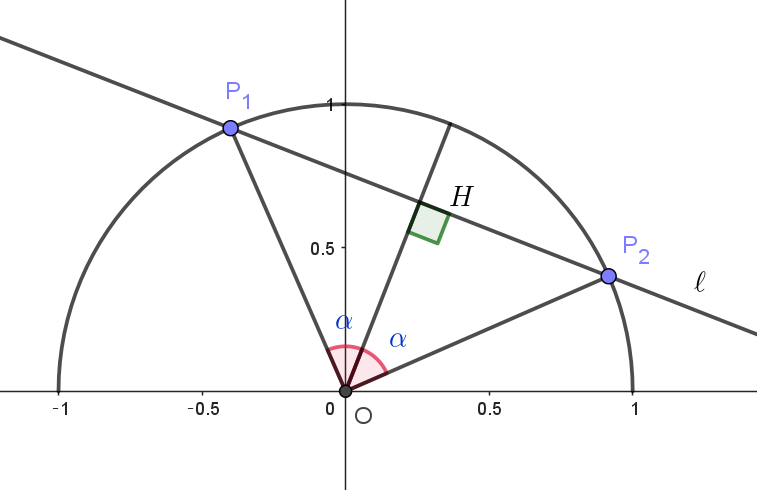
$OP_2=1,\quad \triangle HOP_2 \ は直角三角形だから$

$OH=OP_2\cos \alpha =\cos \alpha$

$一方、H\big(\dfrac{\sqrt{2}}{2}\cos (\theta + \dfrac{\pi}{4}),\ \dfrac{\sqrt{2}}{2}\sin (\theta + \dfrac{\pi}{4})\big)\quad だから$

$OH=\cfrac{\sqrt{2}}{2}$

$よって \quad \cos \alpha=\cfrac{\sqrt{2}}{2}$

$0 < \alpha < \theta + \cfrac{\pi}{4}<\cfrac{\pi}{2}+\cfrac{\pi}{4}=\cfrac{3}{4}\pi \quad だから \quad \alpha =\cfrac{\pi}{4}$

$\triangle HOP_1 \ \ と \ \ \triangle HOP_2 \quad において$

$\angle OHP_1 =\angle OHP_2 =90°\quad だからともに直角三角形$

$点P_1\ と \ P_2 \ は半円 \ C\ 上の点だから \quad OP_1=OP_2 $

$OH \ \ は共通$

$よって \quad \triangle HOP_1 \equiv \triangle HOP_2 $

$ゆえに \quad \angle HOP_1 = \angle HOP_2 =\cfrac{\pi}{4}$

$したがって \quad \triangle HOP_1,\ \ \triangle HOP_2 \ \ はいずれも直角二等辺三角形である。$


(2)


$OH\ と \ x\ 軸の正方向となす角は \ \ \theta +\cfrac{\pi}{4} , \quad \alpha=\cfrac{\pi}{4} \quad だから$

$OP_2 \ と \ x\ 軸の正方向となす角は \quad \theta $

$P_1(x_1,\ y_1),\quad P_2(x_2,\ y_2)\quad とおくと$

$x_2=\cos \theta , \quad y_2=\sin \theta$

$x_1=\cos (\dfrac{\pi}{2}+\theta)=-\sin \theta , \quad y_2=\sin (\dfrac{\pi}{2}+\theta)=\cos \theta$

$よって \quad P_1(-\sin \theta,\ \cos \theta), \quad P_2(\cos \theta, \ \sin \theta)$


(3)

　

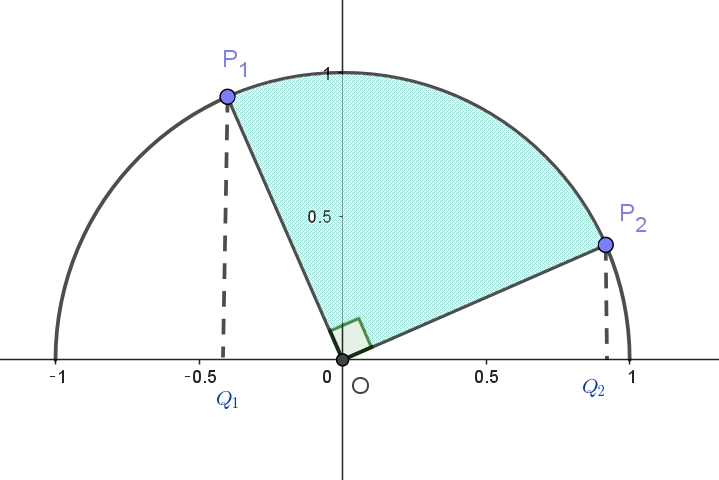
$点P_1,\ P_2 \ から \ x\ 軸に下した垂線をそれぞれ \ \ P_1Q_1,\ \ P_2Q_2 \ \ とする。$

$\triangle OP_1Q_1,\ \ \triangle OP_2Q_2 ,\ \ 弧P_1P_2\ \ を\ x\ 軸の周りに \ 1\ 回転させてできる$

$立体の体積をそれぞれ \ \ V_1,\ V_2 ,\ V_3 \ \ とする。$

$V_1=\cfrac{1}{3}\pi y_1^2 \times (-q_1)=\cfrac{\pi}{3}\cos ^2\theta \sin \theta$

$V_2=\cfrac{1}{3}\pi y_2^2 \times q_2=\cfrac{\pi}{3}\sin ^2\theta \cos \theta$

\begin{eqnarray*} V_3 &=&\pi \int _{q_1}^{q_2} (1-x^2)dx\\ \\ &=&\pi\big[x-\dfrac{x^3}{3}\big]_{-\sin \theta}^{\cos \theta}\\ \\ &=&\pi\big\{\cos \theta + \sin \theta -\dfrac{1}{3}(\cos ^3 \theta +\sin ^3\theta)\big\}\\ \\ &=&\cfrac{\pi}{3}\big\{3(\cos \theta + \sin \theta) -(\cos ^3 \theta +\sin ^3\theta)\big\}\\ \end{eqnarray*}
\begin{eqnarray*} V &=&V_3-V_1-V_2\\ \\ &=&\cfrac{\pi}{3}\big\{3(\cos \theta + \sin \theta) -(\cos ^3 \theta +\sin ^3\theta)\big\}- \cfrac{\pi}{3}\cos ^2\theta \sin \theta - \cfrac{\pi}{3}\sin ^2\theta \cos \theta \\ \\ &=&\cfrac{\pi}{3}\big\{3(\cos \theta + \sin \theta) -\cos \theta (\cos ^2 \theta +\sin ^2\theta) - \sin \theta(\sin ^2\theta +\cos ^2\theta)\big\} \\ \\ &=&\cfrac{\pi}{3}\big\{3(\cos \theta + \sin \theta) -\cos \theta - \sin \theta \big\} \\ \\ &=&\cfrac{2}{3}\pi (\sin \theta + \cos \theta) \\ \end{eqnarray*} $よって \quad \cfrac{V}{\sin \theta + \cos \theta }=\cfrac{2}{3}\pi \quad だから \ \theta \ によらず一定である。$


(4)


$V=\cfrac{2}{3}\pi (\sin \theta + \cos \theta) =\cfrac{2\sqrt{2}}{3}\pi \sin (\theta + \dfrac{\pi}{4})$

$0 \leqq \theta \leqq \dfrac{\pi}{2} \quad より \quad \cfrac{\pi}{4} \leqq \theta + \cfrac{\pi}{4} \leqq \cfrac{3}{4}\pi $

$\sin (\theta + \dfrac{\pi}{4}) \ \ は \ \ \theta + \dfrac{\pi}{4}=\cfrac{\pi}{2} \ \ のとき、すなわち \ \ \theta=\cfrac{\pi}{4} \ \ のとき 最大値 \ 1\ をとるから $

$V\ は、\theta=\cfrac{\pi}{4}\ \ のとき \ 最大値 \ \ \cfrac{2\sqrt{2}}{3}\pi \ \ をとる。$


ページの先頭へ↑



メインメニュー　に戻る