埼玉大学(理系) 2024年 問題1
$複素数 \ z\ に対して複素数 \ w\ を \ w=\dfrac{z+3}{z+1}\ により定める。ただし \ z \ne -1 \ とする。次の問いに答えよ。$
$(1)\ \ w \ne 1 \ を示し、z\ を \ w\ を用いて表せ。$
$(2)\ \ z\ の虚部が正のとき、w\ の虚部は負であることを示せ。$
$(3)\ \ (1+i)z \ の実部が \ 0\ のとき、w\ のとり得る値の範囲を求め、それを複素数平面上に図示せよ。$
(1)
$w=\dfrac{z+3}{z+1} \quad より \quad w(z+1)=z+3 $
$z(w-1)=-w+3 $
$w=1\ \ とすると \quad 左辺=0,\quad 右辺=2 \quad となって不合理であるから$
$w \ne 1$
$よって \quad z=\cfrac{-w+3}{w-1}$
(2)
$z=a+bi\ \ (a,\ b\ は実数)\ \ とおくと \ z\ の虚部が正だから \quad b > 0$
$このとき$
\begin{eqnarray*} w &=&\cfrac{z+3}{z+1}\\ \\ &=&\cfrac{a+3+bi}{a+1+bi}\\ \\ &=&\cfrac{(a+3+bi)(a+1-bi)}{(a+1+bi)(a+1-bi)}\\ \\ &=&\cfrac{(a+3)(a+1)+b^2+i(b(a+1)-b(a+3))}{(a+1)^2+b^2}\\ \\ &=&\cfrac{(a+3)(a+1)+b^2+i(-2b)}{(a+1)^2+b^2}\\ \end{eqnarray*} $よって w\ の虚部は負である。$
(3)
$z=a+bi\ \ (a,\ b\ は実数)\ \ とおくと$
$(1+i)z=(1+i)(a+bi)=a-b+i(a+b)$
$この実部が \ 0\ だから \ \ a=b \quad よって \quad z=a+ai=a(1+i)$
$(1)より \quad z=\cfrac{-w+3}{w-1} \quad だから$
$a(1+i)=\cfrac{-w+3}{w-1}$
$a=\cfrac{-w+3}{(1+i)(w-1)}$
$a \ は実数だから \quad a=\overline{a}$
$\cfrac{-w+3}{(1+i)(w-1)}=\cfrac{-\overline{w}+3}{(1-i)(\overline{w}-1)}$
$(1-i)(\overline{w}-1)(-w+3)=(1+i)(w-1)(-\overline{w}+3) \hspace{15em}(*)$
$(\overline{w}-1)(-w+3)-i(\overline{w}-1)(-w+3)=(w-1)(-\overline{w}+3)+i(w-1)(-\overline{w}+3)$
$-w \overline{w} +w +3\overline{w} -3-i(-w \overline{w}+w+ 3\overline{w}-3) =-w \overline{w} +3w +\overline{w} -3+i(-w \overline{w}+3w+\overline{w}-3)$
$w -\overline{w} -i(w \overline{w}-2w -2\overline{w}+3)=0$
$i(w -\overline{w})+ w \overline{w}-2w -2\overline{w}+3=0$
$w \overline{w}-(2-i)w -(2+i)\overline{w}+3=0$
$(w -(2+i))(\overline{w}-(2-i))=2$
$(w -(2+i))(\overline{w-(2+i)})=2$
$|w -(2+i)|^2=2$
$|w -(2+i)|=\sqrt{2}$
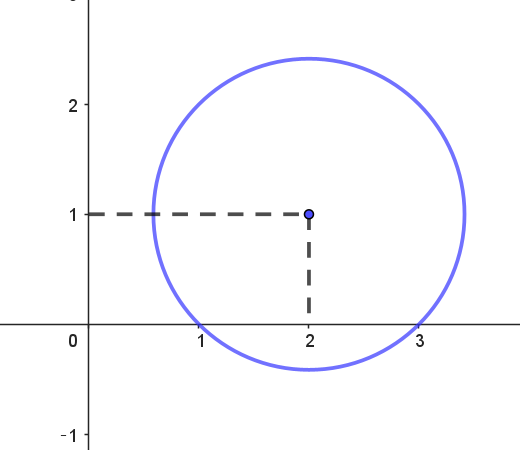
$よって \quad w\ は \ 2+i \ を中心として、半径 \ \sqrt{2} \ の円をえがく。$
$(別解)$
$(1+i)z \ の実部が \ 0\ だからこれは純虚数である。$
$したがって \quad (1+i)z+(1-i)\overline{z}=0$
$両辺に \ i\ をかけて$
$(i-1)z+(i+1)\overline{z}=0$
$(1-i)z=(1+i)\overline{z}$
$この式に z=\cfrac{-w+3}{w-1} を代入して$
$(1-i) \times \cfrac{-w+3}{w-1}=(1+i) \times \cfrac{-\overline{w}+3}{\overline{w}-1}$
$(1-i)(\overline{w}-1)(-w+3)=(1+i)(w-1)(-\overline{w}+3)$
$これで上の解答の(*)と同じ式になりました$
メインメニュー に戻る