立方体を、その辺上に与えられた3点を通る平面で切った切り口の図形
求め方の基本事項は
(1)立方体の同一面上にある2点は直線で結ぶことができる。
(2)立方体の向かい合う2つの面上の線分は互いに平行である。
の2点であるが、具体的に切断面を求めるには、立方体の面上に乗っている切断面の辺の
本数によって分類できる。
立方体の面上にのっている切断面の辺の個数による分類
面上に3本の線分が引ける場合
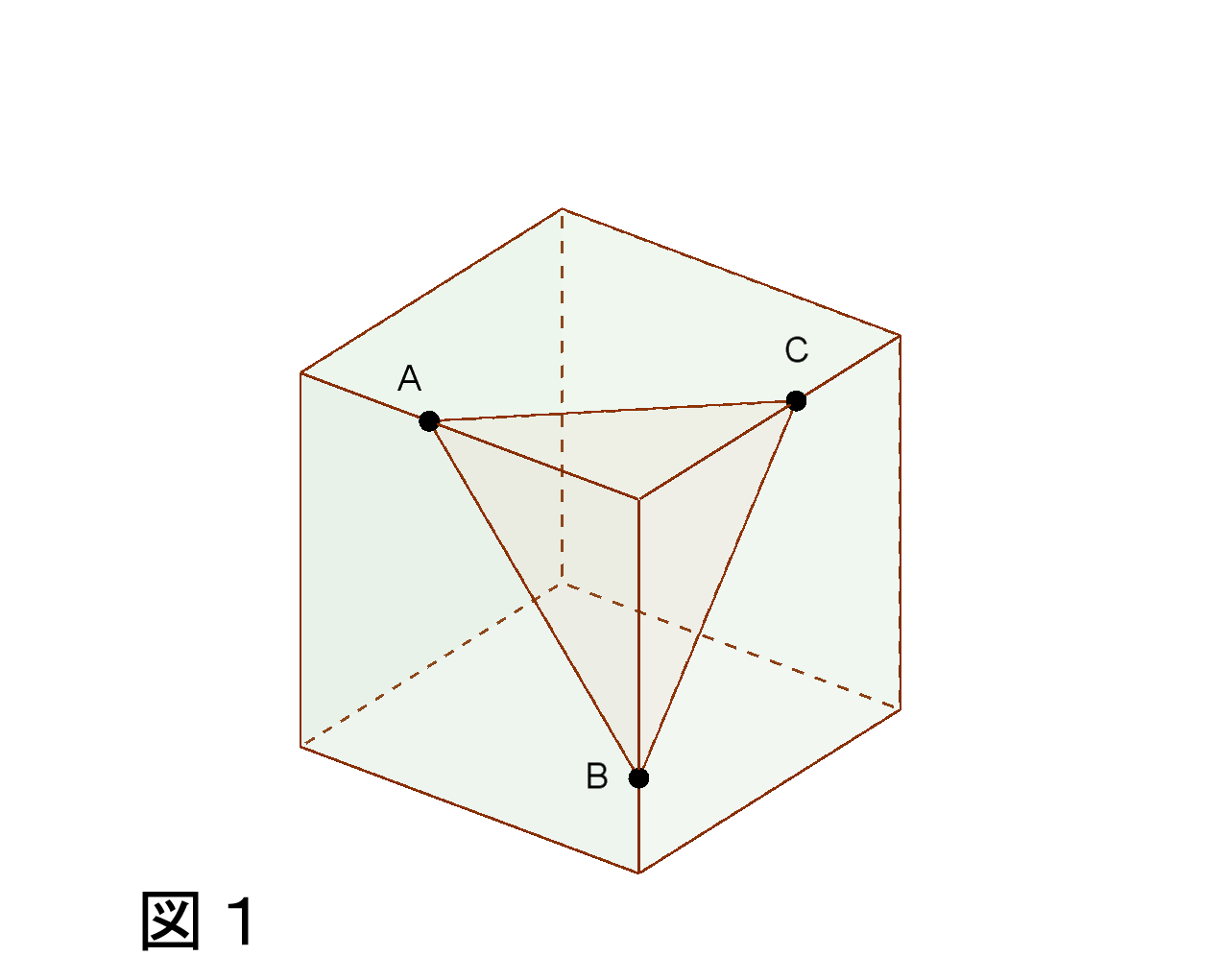
図1のような3点A、B、Cを通る平面で切った切り口の求め方は
基本(1)により同一面上にある2点をそれぞれ直線で結べばよい。
切り口は三角形である。
面上に2本の線分が引ける場合
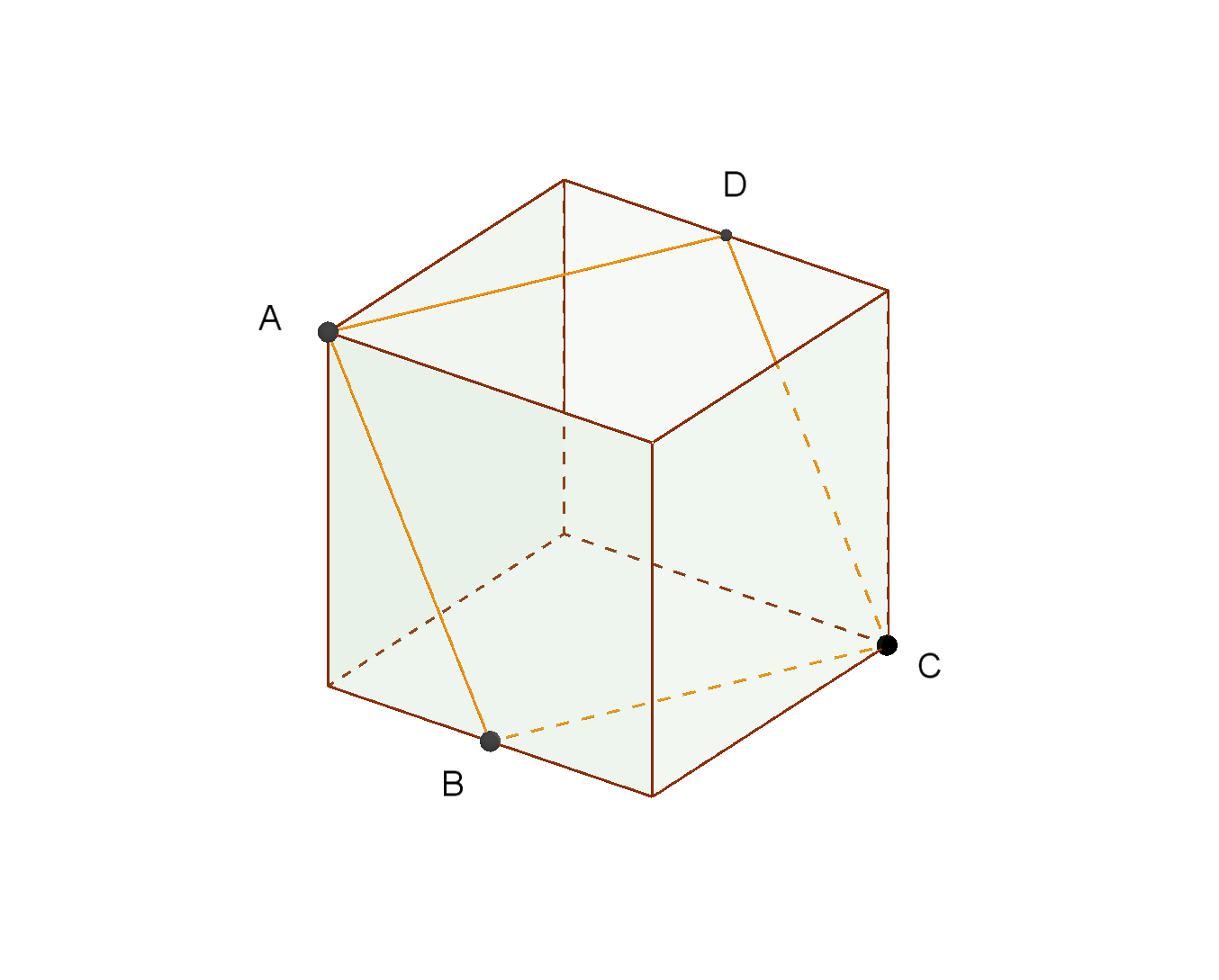
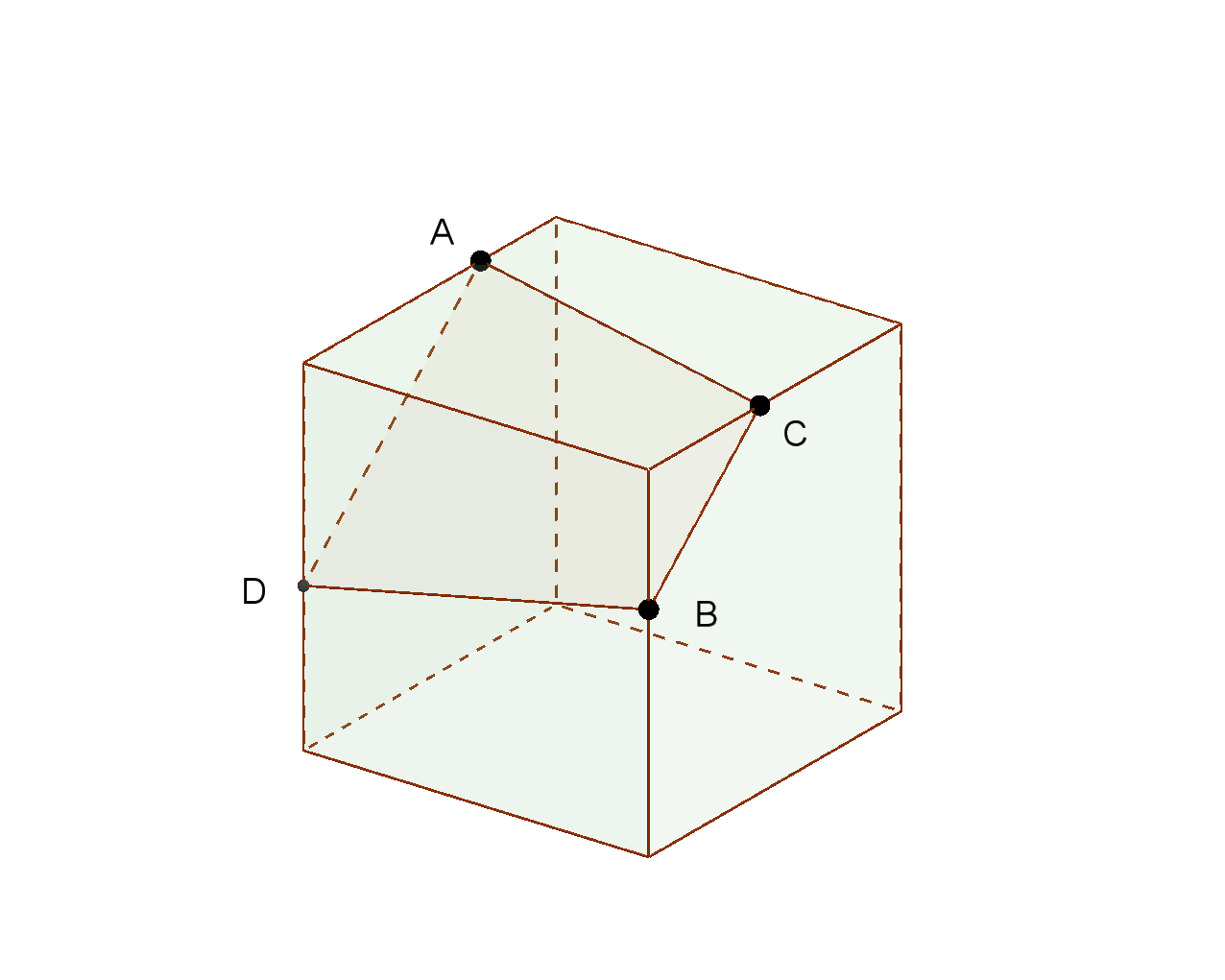
図2のような3点A、B、Cを通る平面で切った切り口の求め方は
まず、(1)により同一面上にある2点ABとBCをそれぞれ直線で結ぶ。
次に、(2)によりAB // CD となるように点Dをとる。(BC // ADでもよい)
切り口は四角形であることがわかる。
図3のような3点A、B、Cを通る平面で切った切り口の求め方は
まず、(1)により同一面上にある2点ACとBCをそれぞれ直線で結ぶ。
次に、(2)によりCB // AD となるように点Dをとる。
BDを結ぶ。
切り口は四角形であることがわかる。
面上に1本の線分が引ける場合
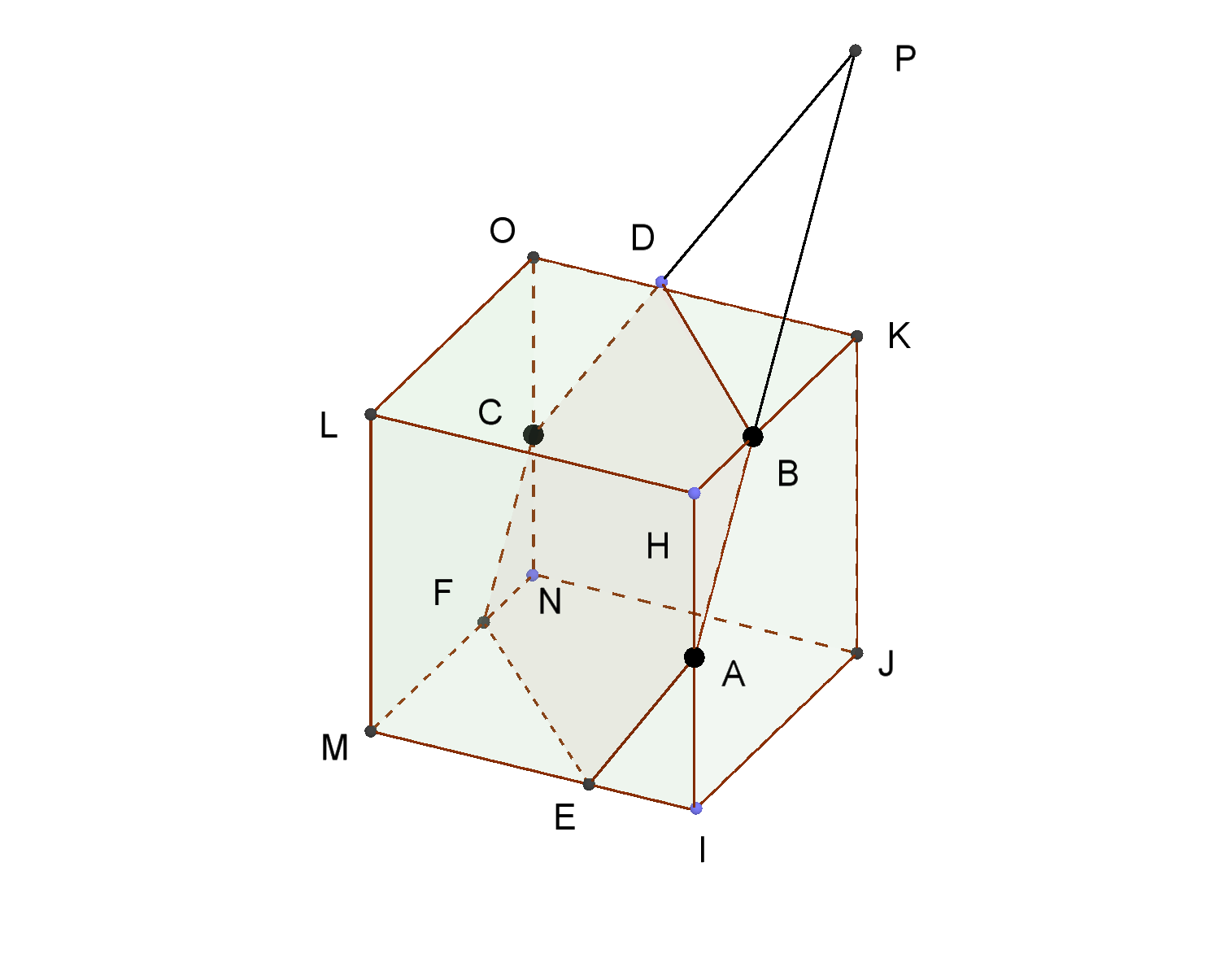
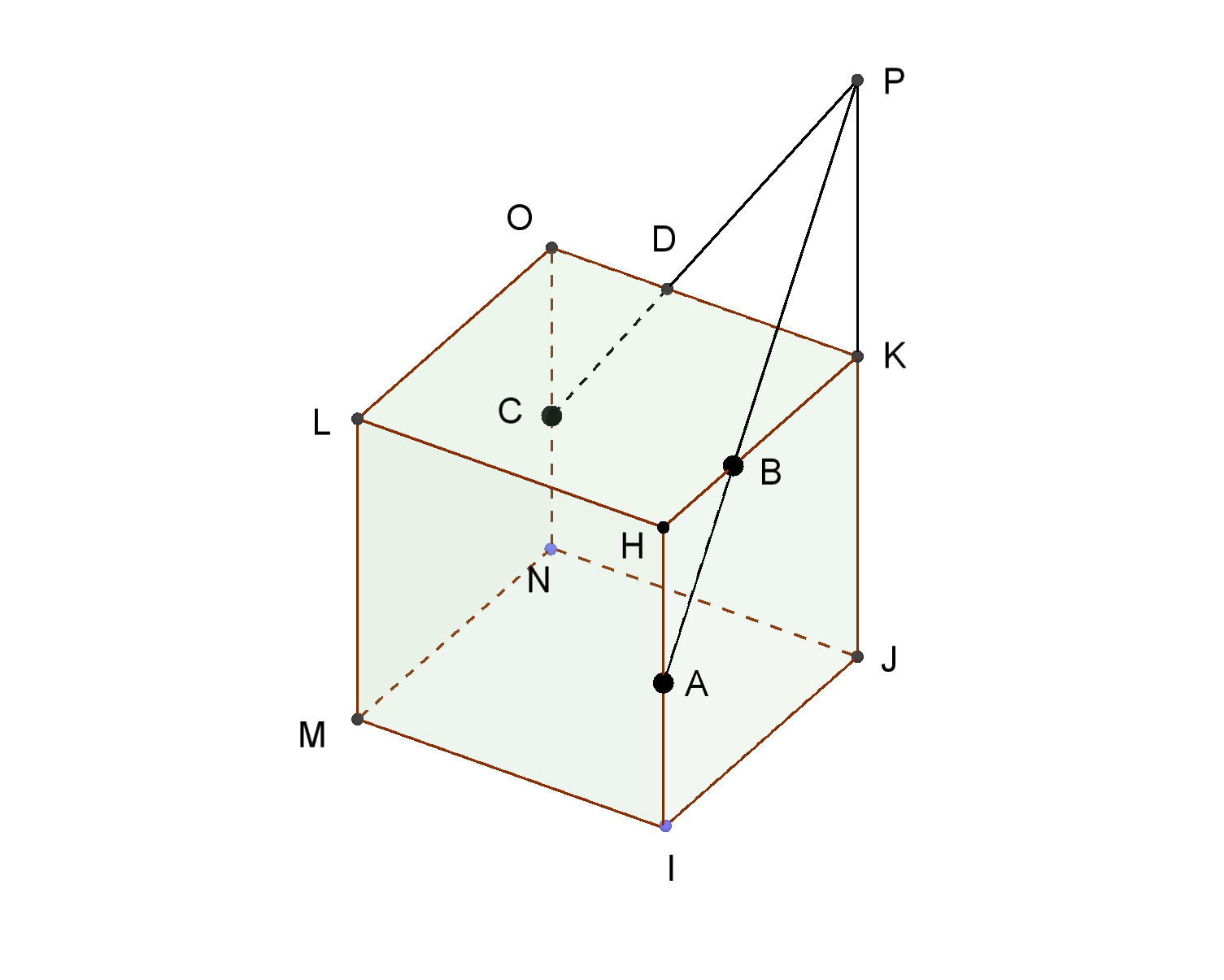
図4のような3点A、B、Cを通る平面で切った切り口の求め方は
まず、(1)により同一面上にある2点ABを直線で結ぶ。
切断面は直線AB上かつCD(点Dは未定)上にあるから、交点をPとする。
点Pは直線ABがのっている平面HIJK上にあり、かつCDがのっている平面ONJK上にも
あるから、その交線JK上にあることになる。
すなわち直線ABとJKの交点がPである。(図5)
そこで、この点PとCを結べば,点Dが求まるので、BDを結ぶ。
次は、線分DCが平面ONJK上にあることに注意して、これに平行な平面LMIH上にとる。
同様にして線分BAに平行に線分FCをとり、点E、Fを結ぶ。
切り口は六角形である。
なお、点Pを決めるのに、図5のように、点AとBを結び、延長する。
辺JKの延長との交点をPとする。この点Pは平面ONJK上にもあるから、その上にある点Cと結ぶ。
(以下同じ)
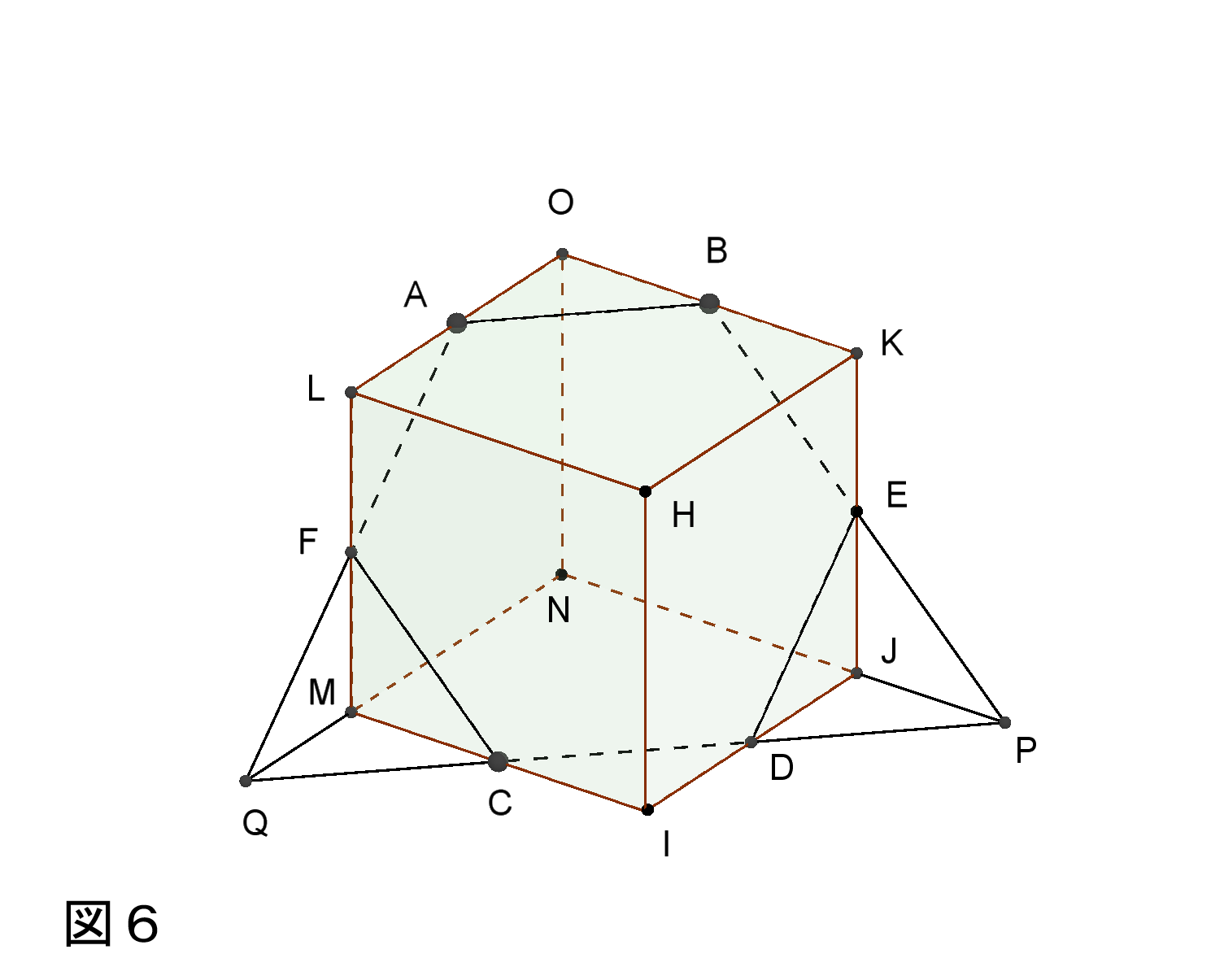
図6のような3点A、B、Cを通る平面で切った切り口の求め方は
AB//CDとなるように点Dをとる。
直線CDと辺NJの延長の交点をPとし、BP,CPを結ぶ。
同様に、直線CDとNMの延長の交点をQとし、QAを結ぶ。
切り口は六角形である。
面上に線分が引けない場合
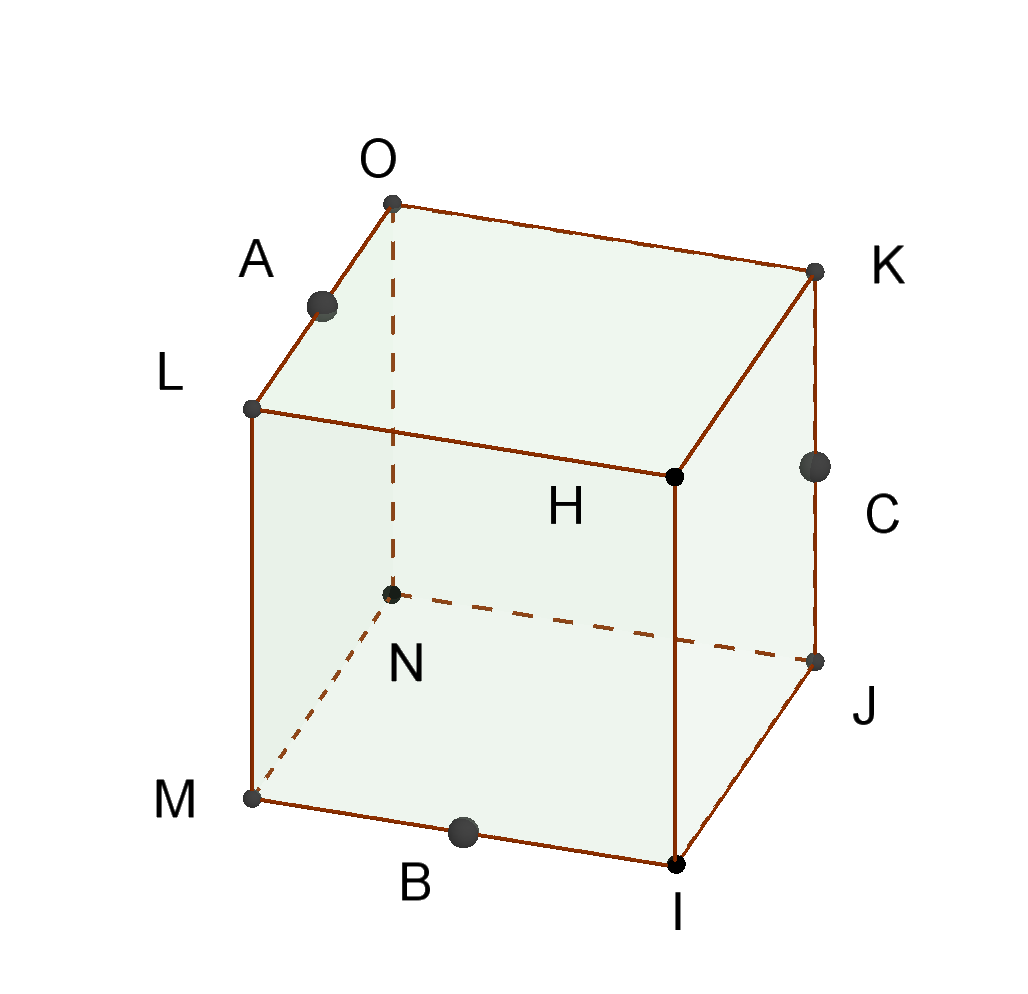
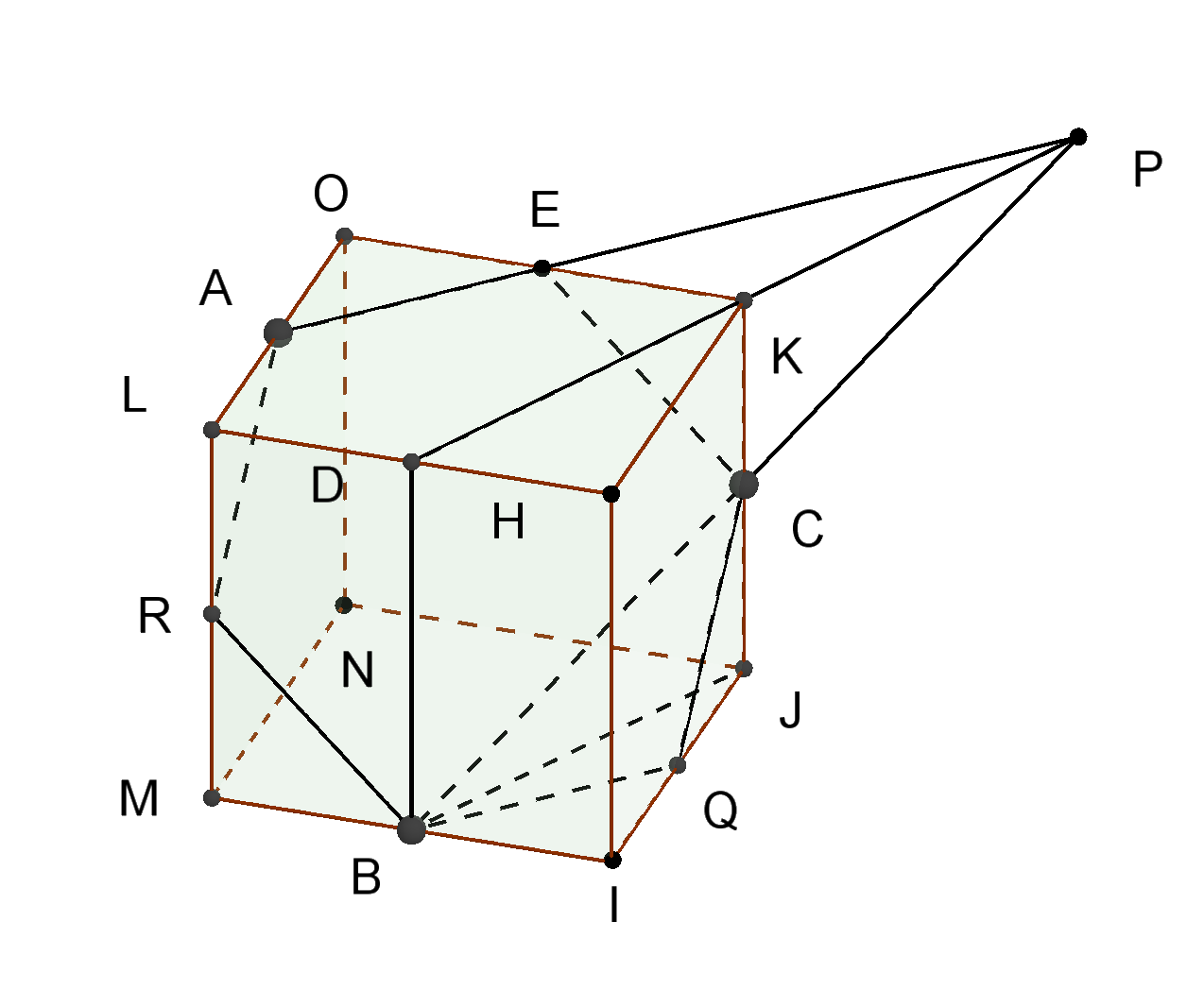
図7のように同一平面上にない3点A、B、Cを通る平面で切った切り口の求めるのは難しい。
この平面を真上から見ると、BCはBJに重なる。そこで、上面でBJに平行にDKをとる。
DKとBCの交点Pをとる。(図8)
点Pは平面ADK(上面)上にあるからPとAを結び交点をEとする。
EとA、EとCを結ぶ。
AE // BQとなるQをとる。CQ // AR となるRをとる。
切り口は6角形であることがわかる。
メインメニュー に戻る