極と極線



$2\ 次極線上にない点 \ P(x_0,\ y_0)\ \ からこの \ 2\ 次極線に引いた \ 2\ 本の接線の接点を結ぶ直線 \ l\ を極線といい、$

$この点 \ P\ を極という。$


$\hspace{3em}$
$\hspace{6em}$


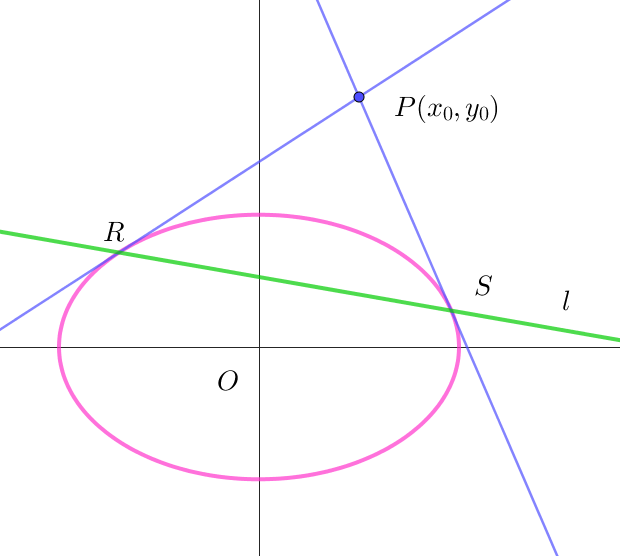
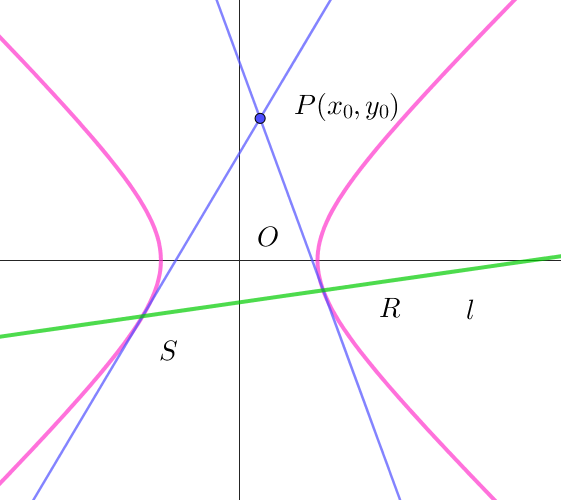
$(1)\ \ 楕円・双曲線の極線$

$\quad 楕円・双曲線 \ \ Ax^2+By^2=1\ \ 上の点 \ R(x_1,\ y_1)、点 \ S(x_2,\ y_2)\ \ における接線は$

$\quad それぞれ \quad Ax_1x+by_1y=1 ,\qquad Ax_2x+By_2y=1 \qquad ($ 2次曲線の接線$をご覧ください)$

$\quad これらが点 \ P(x_0,\ y_0)\ を通るから \quad Ax_1x_0+by_1y_0=1 ,\qquad Ax_2x_0+By_2y_0=1 $

$\quad これは、直線 \ \ Ax_0x+By_0y=1\ \ が点 \ R(x_1,\ y_1)、点 \ S(x_2,\ y_2)\ \ を通ることを示している。$

$\quad したがって \quad l:Ax_0x+By_0y=1 \ \ が点 \ P(x_0,\ y_0)\ \ を極とする極線である。$


　
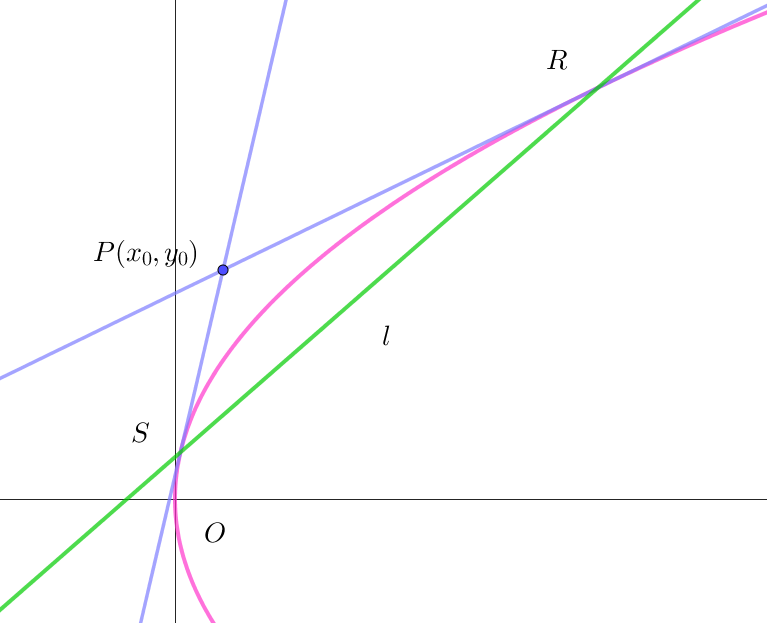
$(2)\ \ 放物線の極線$

$\quad 放物線 \ \ y^2=4px \ \ 上の点 \ R(x_1,\ y_1)、点 \ S(x_2,\ y_2)\ \ における接線は$

$\quad それぞれ \quad y_1y=2p(x+x_1) ,\qquad y_2y=2p(x +x_2)$

$\quad ($ 2次曲線の接線$をご覧ください)$

$\quad これらが点 \ P(x_0,\ y_0)\ を通るから$

$\qquad y_1y_0=2p(x_0+x_1) ,\qquad y_2y_0=2p(x_0 +x_2) $

$\quad これは、直線 \ \ y_0y=2p(x+x_0)\ \ が点 \ R(x_1,\ y_1)、点 \ S(x_2,\ y_2)\ を通ることを示している。$

$\quad したがって \quad l:y_0y=2p(x+x_0)\ \ が点 \ P(x_0,\ y_0)\ を極とする極線である。$


$定理 \quad 2\ 次曲線上にない点 \ P(x_0,\ y_0)\ を極にもつ極線 \ l\ 上に点 \ Q(x_1,\ y_1)\ をとる。$

$\hspace{3em} このとき、点 \ Q\ を極とする極線 \ m\ は点 \ P\ を通る。$



$\hspace{3em}$
$\hspace{6em}$


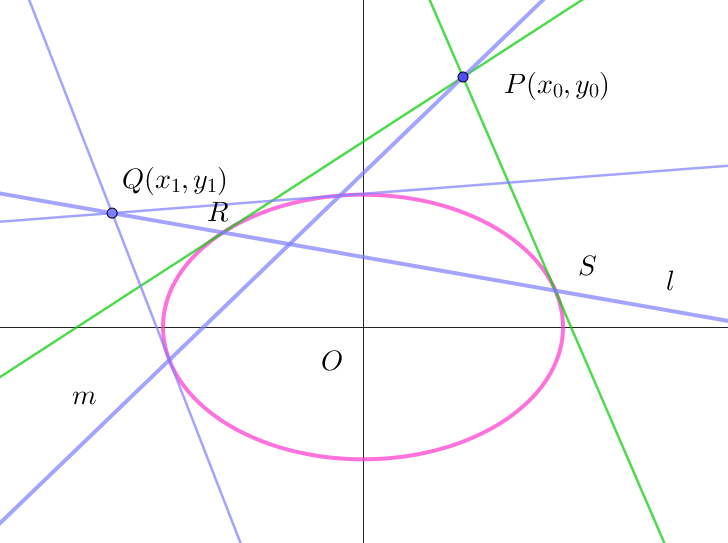
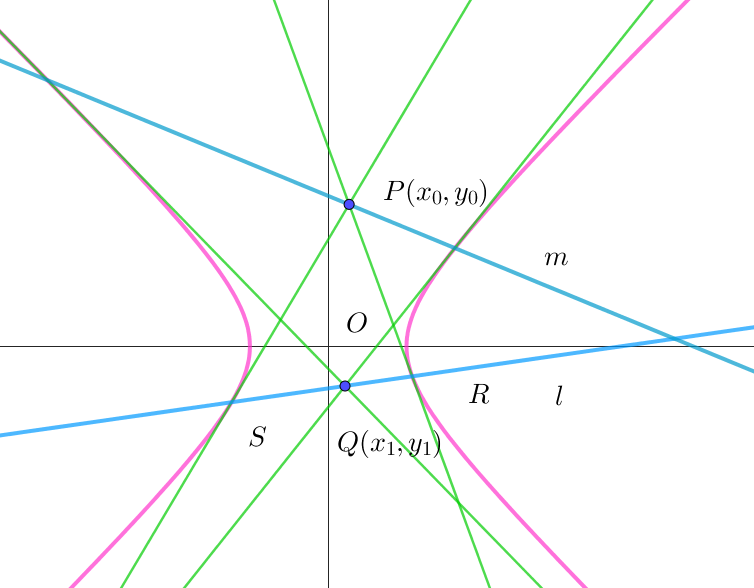
$(1)\ \ 楕円・双曲線の場合$

$(証明)$

$\quad 点 \ P(x_0,\ y_0)\ を極にもつ極線 \ \ l:Ax_0x+By_0y=1 \ \ 上の点を \ Q(x_3,\ y_3)\ とすると$

$\qquad Ax_0x_3+By_0y_3=1 $

$\quad 一方 \quad Q(x_3,\ y_3)\ を極とする極線は \quad m:Ax_3x+By_3y=1 \quad だから 点 \ P(x_0,\ y_0) \ はこの極線 \ m\ 上にある。$



　
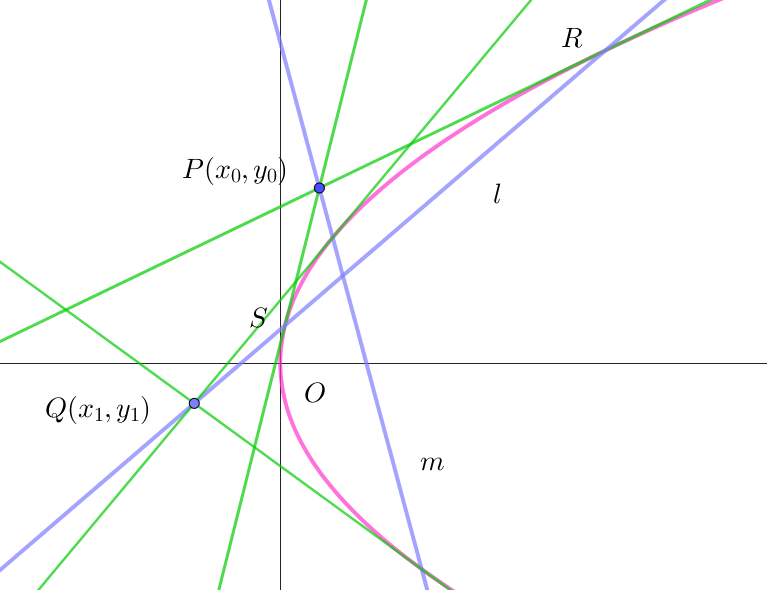
$(2)\ \ 放物線の場合$

$(証明)$

$\quad 点 \ P(x_0,\ y_0)\ を極にもつ極線 \quad l:y_0y=2p(x+x_0)\ \ 上の点を$

$\quad Q(x_3,\ y_3)\ \ とすると \qquad y_0y_3=2p(x_3+x_0) $

$\quad 一方 \quad Q(x_3,\ y_3)\ を極とする極線は \quad m: y_3y=2p(x+x_3) \quad だから 点 \ P(x_0,\ y_0)\ はこの極線 \ m\ 上にある。$



ページの先頭へ↑



2次曲線メニュー　に戻る


メインメニュー　に戻る