四分円を用いたモンテカルロ法
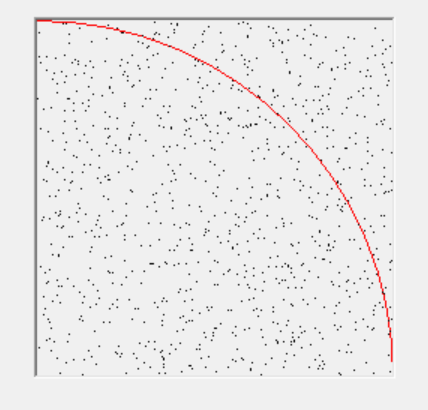
$一辺1の正方形に内接する四分円に対して、x座標、$
$y座標をそれぞれ乱数で与えた点が四分円の中に入る$
$かどうかをカウントする方法もある。$
$面積比=\cfrac{\cfrac{1}{4}×\pi×1^2}{1^2}=\cfrac{\pi}{4}$
$点を打つ回数をN、そのうち四分円に入った回数をkと$
$する。Nを十分大きくとれば、相対度数 \cfrac{k}{N} は確率と$
$見なせるから$
$\hspace{3em} \cfrac{\pi}{4}=\cfrac{k}{N} より \pi=4×\cfrac{k}{N}$
$Visual Basic を用いて、N=1000 を1セットとして10セット繰り返した結果が下表です。$
$kは累積度数です。$
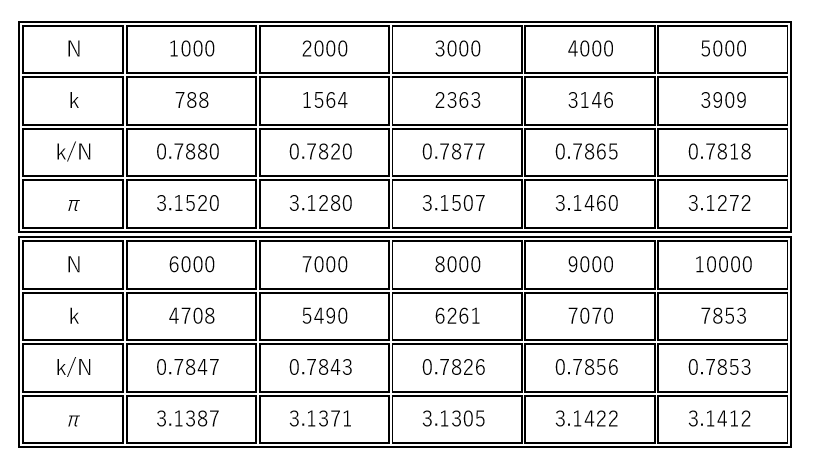
$\pi の値が3.141まで出でました。おそらくビュッフォンの針では関数\ \sin \theta \ を使うが、$
$この方法は\quad x^2+y^2\leqq 1 \quad しか使っていないからと思われます。$
円周率 $π$ の話 に戻る
メインメニュー に戻る