大阪大学(理系) 2025年　問題3


$座標空間に3\ 点O(0,\ 0,\ 0),\ \ A(0,\ 1,\ 1),\ \ P(x,\ y,\ 0)\ \ がある。\angle OAP=30°\ \ かつ \ \ y \geqq 0 \ \ を満たすように$
$点P\ が動くとき、(x+1)(y+1)\ \ の最大値と最小値を求めよ。$

　

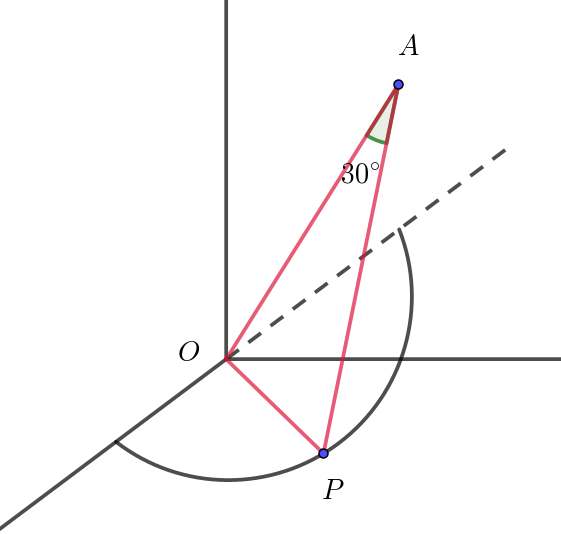
$OA^2=1^2+1^2=2,\quad OP^2=x^2+y^2,\quad AP^2=x^2+(y-1)^2+1$

$\triangle OAP \ \ に余弦定理を用いて$

$OP^2=OA^2+AP^2-2OA \cdot AP \cdot \cos 30°$

$x^2+y^2=2+\{x^2+(y-1)^2+1\}-2\sqrt{2}\sqrt{x^2+(y-1)^2+1} \times \dfrac{\sqrt{3}}{2}$

$4-2y=\sqrt{6}\sqrt{x^2+(y-1)^2+1} $

$(4-2y)^2=6\{x^2+(y-1)^2+1\}$

$3x^2+y^2+2y=2$

$3x^2+(y+1)^2=3 \hspace{5em}①$

$よって 点P\ は楕円をえがく。$

　

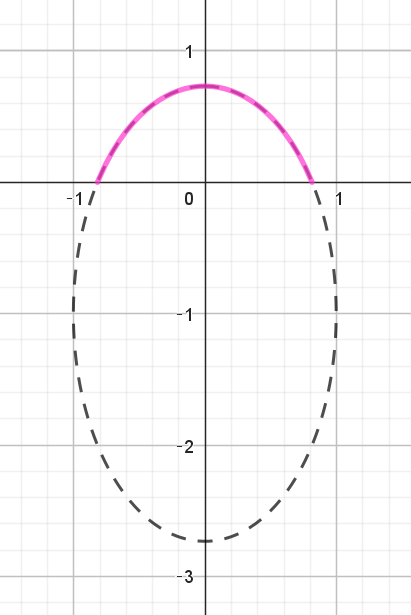
$y \geqq 0 \ \ だから \quad 　(y+1)^2=3-3x^2 \geqq 1 \ \ より \quad 3x^2 \leqq 2$

$よって \quad x^2 \leqq \dfrac{2}{3} \qquad \therefore \ \ -\dfrac{\sqrt{6}}{3} \leqq x \leqq \dfrac{\sqrt{6}}{3}$

$(x+1)(y+1)=k \quad とおくと$

$x+1=0 \ \ すなわち \quad x=-1 \ \ のとき①より \quad y+1=0 \qquad y=-1 $

$ところが \ \ y \geqq 0 \ \ だから \quad x+1 \ne 0$

$y+1=\dfrac{k}{x+1} \ \ これを①に代入して$

$3x^2+\dfrac{k^2}{(x+1)^2}=3 $

$3x^2(x+1)^2+k^2=3(x+1)^2$

$-3(x^4+2x^3-2x-1)=k^2$

$f(x)=-3(x^4+2x^3-2x-1) \quad とおくと$

　

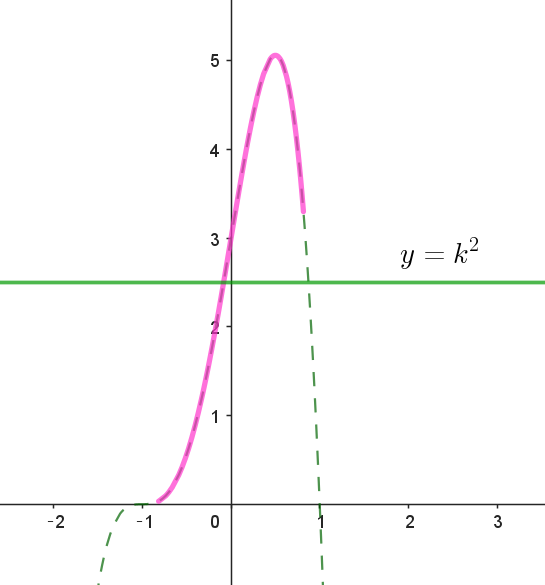
\begin{eqnarray*} f'(x) &=&-3(4x^3+6x^2-2)\\ \\ &=&-6(2x^3+3x^2-1)\\ \\ &=&-6(x+1)(2x^2+x-1)\\ \\ &=&-6(x+1)^2(2x-1) \end{eqnarray*} $f'(x)=0 \ \ より \quad x=\dfrac{1}{2}$

$増減表$
\[ \begin{array}{c||c|c|c|c|c} x & -\dfrac{\sqrt{6}}{3} & \cdots & \dfrac{1}{2} & \cdots & \dfrac{\sqrt{6}}{3} \\ \hline f'(x) & & + & 0 & - & \\ \hline f(x) & & \nearrow & 極大 & \searrow & \\ \end{array} \]
$f(x)\ は \ \ x=\dfrac{1}{2}\ \ のとき \ \ 極大かつ最大となり最大値は$

$\quad f(\dfrac{1}{2})=-3\big(\dfrac{1}{16}+2 \times \dfrac{1}{8} -2 \times \dfrac{1}{2} -1\big)=\dfrac{81}{16}$

$端点の値は$

$\quad f(-\dfrac{\sqrt{6}}{3})=-3\big(\dfrac{4}{9}-2 \times \dfrac{2}{3}\times \dfrac{\sqrt{6}}{3}+2\times \dfrac{\sqrt{6}}{3}-1\big)= -3\big(-\dfrac{5}{9}+\dfrac{2}{3} \times \dfrac{\sqrt{6}}{3}\big)=\dfrac{5-2\sqrt{6}}{3}$

$\quad f(\dfrac{\sqrt{6}}{3})=-3\big(\dfrac{4}{9}+2 \times \dfrac{2}{3}\times \dfrac{\sqrt{6}}{3}-2\times \dfrac{\sqrt{6}}{3}-1\big)= 3\big(\dfrac{5}{9}+\dfrac{2}{3} \times \dfrac{\sqrt{6}}{3}\big)=\dfrac{5+2\sqrt{6}}{3}$

$f(x)=k^2 \ \ を満たす \ x\ は \ \ y=f(x) \ と \ y=k^2 \ のグラフの交点の \ x\ 座標だから、k\ の最大、最小は$

$x=\dfrac{1}{2} \ \ のとき \ \ 最大となり最大値は \quad k=\sqrt{\dfrac{81}{16}}=\dfrac{9}{4}$

$x=-\dfrac{\sqrt{6}}{3} \ \ のとき \ \ 最小となり最小値は \quad k=\sqrt{\dfrac{5-2\sqrt{6}}{3}}=\sqrt{\dfrac{(\sqrt{3}-\sqrt{2})^2}{3}}=\dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{3}}=\dfrac{3-\sqrt{6}}{3}$

$なお①に代入して$

$x=\dfrac{1}{2} \ \ のとき \quad (y+1)^2=3-3 \times \dfrac{1}{4}=\dfrac{9}{4} \quad だから \quad y=\dfrac{1}{2}$

$x=-\dfrac{\sqrt{6}}{3} \ \ のとき \quad (y+1)^2=3-3 \times \dfrac{2}{3}=1 \quad だから \quad y=0$

$したがって \quad (x+1)(y+1) \ \ は$

$x=y=\dfrac{1}{2} \ \ のとき最大となり、最大値は \quad \dfrac{9}{4}$

$x=-\dfrac{\sqrt{6}}{3},\ \ y=0 \ \ のとき最小となり、最小値は \quad \dfrac{3-\sqrt{6}}{3}$


ページの先頭へ↑



メインメニュー　に戻る