大阪大学(理系) 2024年 問題4
$a > 1 \ \ とする。xy\ 平面において、点(a,\ 0)\ を中心とする半径 \ 1\ の円を \ C\ とする。$
$(1)\ \ 円 \ C\ の \ x \geqq a \ の部分と \ y\ 軸および \ 2\ 直線 \ \ y=1,\ \ y=-1\ \ で囲まれた図形を \ y\ 軸のまわりに \ 1\ 回転$
$\quad してできる回転体の体積 \ V_1\ を求めよ。$
$(2)\ \ 円 \ C\ で囲まれた図形を \ y\ 軸のまわりに \ 1\ 回転してできる回転体の体積を \ V_2\ とする。(1)における$
$\quad V_1\ について、V_1=2V_2\ \ となる \ a\ の値を求めよ。$
(1)
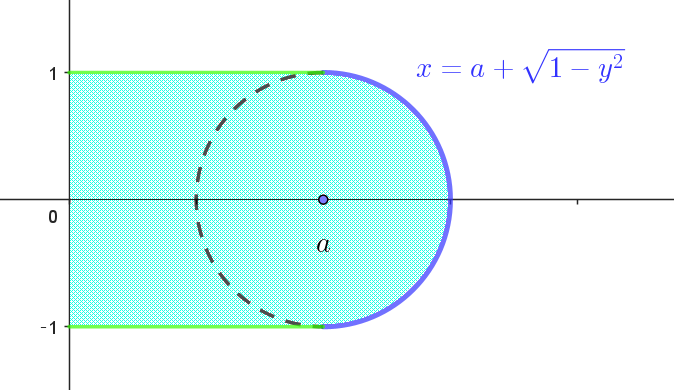
$円 \ C:(x-a)^2+y^2=1 \quad の \ \ x \geqq a \ \ の部分は$
$x=a+\sqrt{1-y^2}$
\begin{eqnarray*}
V_1
&=&2\pi\int_0^1 x^2dy\\
\\
&=&2\pi\int_0^1 (a + \sqrt{1-y^2})^2dy\\
\\
&=&2\pi\int_0^1 \big\{a^2+2a\sqrt{1-y^2}+(1-y^2)\big\}dy\\
\\
&=&2\pi\int_0^1 (a^2+1-y^2)dy + 4\pi a\int_0^1 \sqrt{1-y^2}dy\\
\\
&=&2\pi\big[(a^2+1)y-\dfrac{y^3}{3} \big]_0^1 + 4\pi a \times (半径 \ 1\ の \ 4\ 分円の面積)\\
\\
&=&2\pi \big(a^2+1-\dfrac{1}{3}\big)+ 4\pi a \times \dfrac{\pi}{4}\\
\\
&=&2\pi\big(a^2+\dfrac{2}{3}\big)+ \pi ^2 a\\
\end{eqnarray*}
(2)
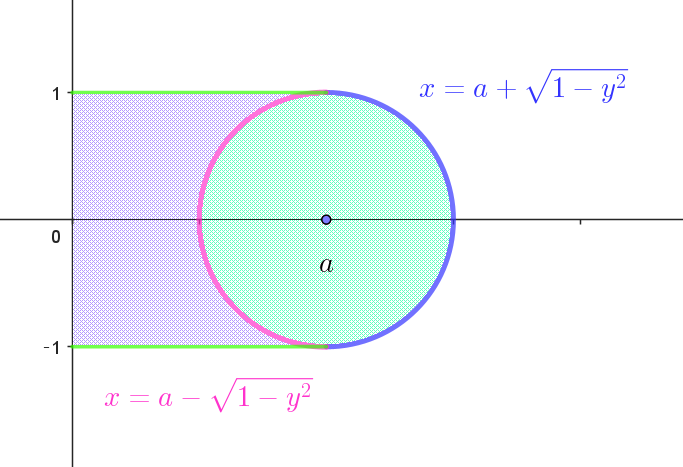
\begin{eqnarray*}
V_2
&=&2\pi\int_0^1 (a + \sqrt{1-y^2})^2dy - 2\pi\int_0^1 (a - \sqrt{1-y^2})^2dy\\
\\
&=&2\pi\int_0^1 \big\{(a + \sqrt{1-y^2})^2 - (a - \sqrt{1-y^2})^2\big\}dy\\
\\
&=&2\pi\int_0^1 4a\sqrt{1-y^2}dy\\
\\
&=&8\pi a \int_0^1 \sqrt{1-y^2}dy\\
\\
&=&8\pi a \times (半径 \ 1\ の \ 4\ 分円の面積)\\
\\
&=&8\pi a \times \dfrac{\pi}{4}\\
\\
&=&2\pi ^2 a\\
\end{eqnarray*}
$(補充)$
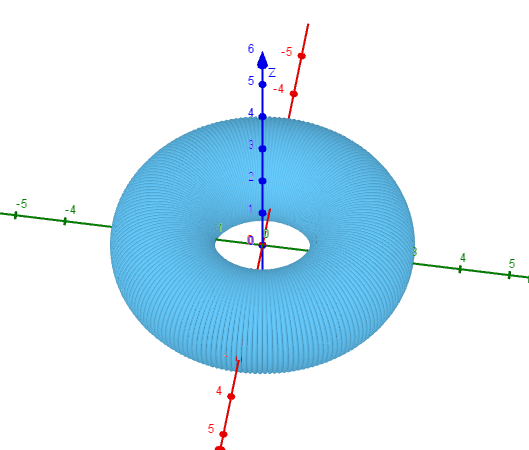
$この回転体はドーナツ状で、トーラス体とか円環体といいます。$
$この体積は、($パップス・ギュルダンの定理$)から$
$回転体の体積=(重心の移動距離) \times (断面積)$
$で求まりますので$
$V_2=2\pi a \times \pi=2\pi ^2 a $
$V_1=2V_2 \quad より$
$2\pi\big(a^2+\dfrac{2}{3}\big)+ \pi ^2 a =4\pi ^2 a$
$2a^2-3\pi a + \cfrac{4}{3}=0$
$6a^2-9\pi a +4=0$
$a=\cfrac{9\pi \pm \sqrt{81\pi ^2-96}}{12}$
$ここで、f(a)=6a^2-9\pi a +4 \quad とおくと$
$f(1)=6-9\pi +4 =10-9\pi < 0$
$したがって中間値の定理より \quad f(a)=0 \ \ の \ 2\ つの実数解のうち$
$1\ つは \ 1\ より大、もう \ 1\ つは \ 1\ より小だから$
$a > 1 \quad より \quad a=\cfrac{9\pi + \sqrt{81\pi ^2-96}}{12}$
メインメニュー に戻る