大阪大学(理系) 2024年 問題1
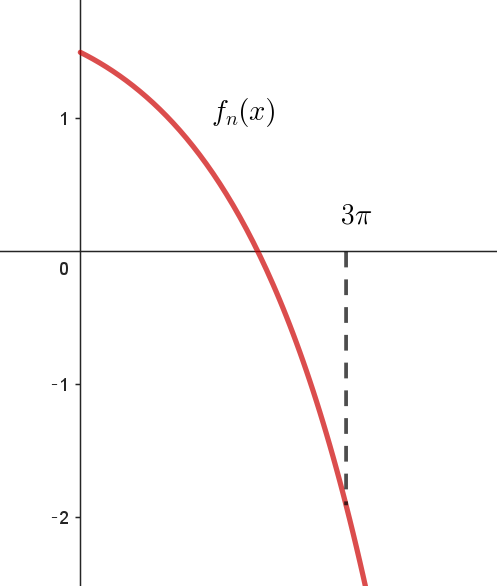
$自然数 \ n\ に対して、関数 \ f_n(x)\ を \ \ f_n(x)=1-\dfrac{1}{2}e^{nx} +\cos \dfrac{x}{3}\ \ (x \geqq 0) \ \ で定める。$
$e\ は自然対数の底である。$
$(1)\ \ 方程式 \ \ f_n(x)=0 \ \ は、ただ \ 1\ つの実数解をもつことを示せ。$
\[(2)\ \ (1)における実数解を \ a_n \ とおくとき、極限値 \ \ \lim_{n \rightarrow \infty} a_n \ \ を求めよ。\]
\[(3)\ \ 極限値 \ \ \lim_{n \rightarrow \infty} na_n \ \ を求めよ。\]
(1)
$f_n(x)=1-\dfrac{1}{2}e^{nx} +\cos \dfrac{x}{3}\ \ (x \geqq 0) \quad より$
$f_n'(x)=-\dfrac{n}{2}e^{nx} -\dfrac{1}{3}\sin \dfrac{x}{3}=-\cfrac{1}{6}(3ne^{nx} +2\sin \dfrac{x}{3})$
$3 \leqq 3ne^x \leqq 3ne^{nx} \quad だから$
$したがって \quad 3ne^{nx} +2\sin \dfrac{x}{3} >0$
$よって \quad f_n'(x) < 0 \quad だから \quad f_n(x)\ \ は単調減少$
$f_n(0)=1-\dfrac{1}{2}+1=\cfrac{3}{2}$
$f_n(3\pi)=1-\dfrac{1}{2}e^{3n\pi} +\cos \pi=-\dfrac{1}{2}e^{3n\pi}<0$
$f_n(x)\ は連続関数だから中間値の定理により、区間 \ (0,\ 3\pi)\ で \ x\ 軸とただ \ 1\ 点で交わる。$
$すなわち \quad 方程式 \ \ f_n(x)=0 \ \ は、ただ \ 1\ つの実数解をもつ。$
(2)
$f_n(a_n)=1-\dfrac{1}{2}e^{na_n} +\cos \dfrac{a_n}{3}=0$
$\dfrac{1}{2}e^{na_n}=1 +\cos \dfrac{a_n}{3}$
$e^{na_n}=2\big(1 +\cos \dfrac{a_n}{3}\big)$
$na_n=\log 2\big(1 +\cos \dfrac{a_n}{3}\big)=\log 2+\log \big(1 +\cos \dfrac{a_n}{3}\big) \hspace{5em}①$
$a_n=\dfrac{1}{n}\big\{\log 2+\log \big(1 +\cos \dfrac{a_n}{3}\big)\big\}$
$\cos \dfrac{a_n}{3} \leqq 1 \quad だから$
$a_n \leqq \dfrac{1}{n}\big\{\log 2+\log (1 + 1)\big\}=\cfrac{2\log 2}{n}$
$(1)より \quad 0 < a_n \quad だから \quad 0 < a_n < \cfrac{2\log 2}{n}$
$n \longrightarrow \infty \quad とすると \quad 右辺 \ \ \longrightarrow 0 $
\[したがって、はさみ打ちの原理により \quad \lim_{n \rightarrow \infty} a_n=0\]
(3)
$n \longrightarrow \infty \quad とすると \quad a_n \longrightarrow 0 \quad だから$
$(2)の① \quad na_n=\log 2+\log \big(1 +\cos \dfrac{a_n}{3}\big) \quad において$
\begin{eqnarray*} & &\lim_{n \rightarrow \infty} na_n\\ \\ &=&\lim_{n \rightarrow \infty} \big(\log 2+\log \big(1 +\cos \dfrac{a_n}{3}\big)\\ \\ &=&\log 2+\log 2\\ \\ &=&2\log 2 \end{eqnarray*}
メインメニュー に戻る