大阪大学(理系) 2018年 問題2
$a,\ b\ を正の実数とし、f(x)=x^4-ax^3+bx^2-ax+1 \ \ とする。$
$(1)\ \ c\ を実数とし、f(x)\ が \ x-c\ で割り切れるとする。このとき、c > 0\ であり、f(x)\ は \ (x-c)(x-\cfrac{1}{c})\ で$
$\quad 割り切れることを示せ。$
$(2)\ \ f(x)\ がある実数 \ s,\ t,\ u,\ v\ を用いて \ \ f(x)=(x-s)(x-t)(x-u)(x-v)\ と因数分解できるとき、$
$\quad a \geqq 4\ が成り立つことを示せ。$
$(3)\ \ a=5\ とする。f(x)\ がある実数 \ s,\ t,\ u,\ v\ を用いて \ \ f(x)=(x-s)(x-t)(x-u)(x-v)\ と因数分解できる$
$\quad ような自然数 \ b\ の値をすべて求めよ。$
$(解説)$
$(1)\ \ は \ f(c)=0 \ \ より \ \ f(\cfrac{1}{c})=0\ を導きます。$
$(2)\ \ は(1)の結果を用いて、f(x)\ を求めます。相加・相乗平均の不等式より \ \ a \geqq 4 \ \ が示せます。$
$(3)\ \ は \ \ p=s+\cfrac{1}{s},\ \ q=u+\cfrac{1}{u}\ \ とでもおいて、b\ を \ p\ の式で表します。$
(1)
$f(x)\ が \ x-c\ で割り切れるから \quad f(c)=c^4-ac^3+bc^2-ac+1=0$
$\quad c^4+bc^2+1=ac^3+ac$
$b > 0 \quad だから 左辺 \ > 0$
$よって \quad ac^3+ac >0 \hspace{3em} ac(c^2+1) > 0$
$a > 0 \quad だから \quad c> 0$
$また$
\begin{eqnarray*} f(\cfrac{1}{c}) &=&\cfrac{1}{c^4}-\cfrac{a}{c^3}+\cfrac{b}{c^2}-\cfrac{a}{c}+1\\ \\ &=&\cfrac{1}{c^4}(1-ac + bc^2 -ac^3 +c^4)\\ \\ &=&\cfrac{1}{c^4}f(c)\\ \\ &=&0\\ \end{eqnarray*} $よって、f(x)\ は \ \ x-\cfrac{1}{c}\ \ で割り切れるから \ \ f(x)\ は \ \ (x-c)(x-\cfrac{1}{c})\ \ で割り切れる。$
(2)
$(1)より \ f(x)\ が \ x-s,\ \ x-u \ \ で割り切れるならば \ \ x-\cfrac{1}{s},\ \ x-\cfrac{1}{u}\ \ でも割り切れるから$
$\qquad t=\cfrac{1}{s},\ v=\cfrac{1}{u} \quad とおけて \quad f(x)=(x-s)(x-\cfrac{1}{s})(x-u)(x-\cfrac{1}{u}) \quad と因数分解される。$
$したがって$
\begin{eqnarray*} f(x) &=&(x-s)(x-\cfrac{1}{s})(x-u)(x-\cfrac{1}{u})\\ \\ &=&\big\{x^2-(s+\cfrac{1}{s})x+1\big\}\big\{x^2-(u+\cfrac{1}{u})x+1\big\}\\ \\ &=&x^4-(s+\cfrac{1}{s}+u+\cfrac{1}{u})x^3+\big\{2+(s+\cfrac{1}{s})(u+\cfrac{1}{u})\big\}x^2-(s+\cfrac{1}{s}+u+\cfrac{1}{u})x+1\\ \\ \end{eqnarray*} $f(x)\ の \ x^3\ の係数を比べて$
$\quad a=s+\cfrac{1}{s}+u+\cfrac{1}{u}$
$(1)より \ s > 0,\ u > 0 \quad だから相加・相乗平均の不等式より$
$\quad a \geqq 2\sqrt{s \times \cfrac{1}{s}} + 2\sqrt{u \times \cfrac{1}{u}}=4$
(3)
$f(x)\ の \ x^3\ と \ x^2\ の係数を比べて$
$\quad a=s+\cfrac{1}{s}+u+\cfrac{1}{u}=5 , \qquad b=2+(s+\cfrac{1}{s})(u+\cfrac{1}{u})$
$s+\cfrac{1}{s}=p,\quad u+\cfrac{1}{u}=q \quad とおくと \quad p \geqq 2,\quad q \geqq 2 \ \ で$
$a=p+q=5 \quad より \quad q=5-p \geqq 2 \quad だから \quad p \leqq 3 \quad よって \quad 2 \leqq p \leqq 3$
\begin{eqnarray*} b &=&2+pq\\ \\ &=&2+p(5-p)\\ \\ &=&-p^2+5p+2\\ \\ &=&-(p-\cfrac{5}{2})^2+\cfrac{33}{4}\\ \end{eqnarray*}
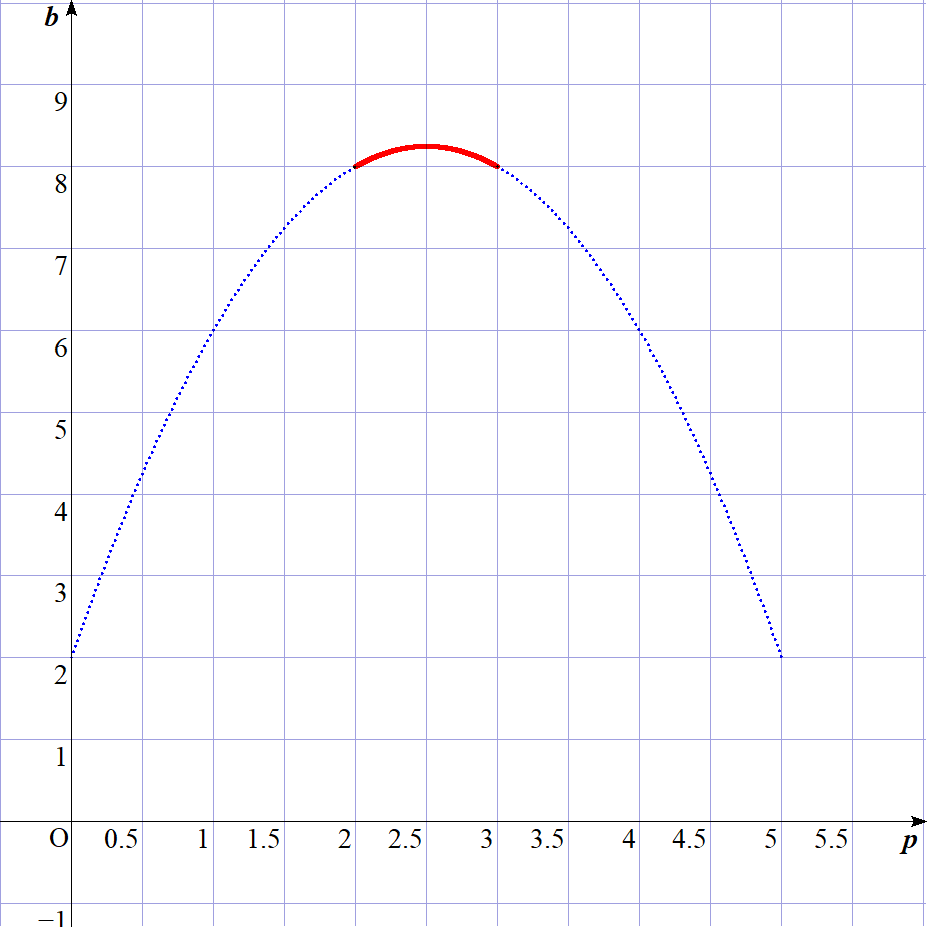
$\quad p=2 \quad のとき \quad b=8$
$\quad p=3 \quad のとき \quad b=8$
$(p,\ b)\ のグラフは右図のとおり$
$\quad 8 \leqq b \leqq \cfrac{33}{4}$
$これを満たす自然数は \quad b=8$
メインメニュー に戻る