大阪大学(理系) 2018年 問題1
$次の問いに答えよ。$
$(1)\ \ x > 0 \ \ の範囲で不等式 \ \ x-\cfrac{x^2}{2} < \log (1+x) < \cfrac{x}{\sqrt{1+x}}\ \ が成り立つことを示せ。$
$(2)\ \ x\ が \ x > 0\ \ の範囲を動くとき、y=\cfrac{1}{\log (1+x)}- \cfrac{1}{x}\ \ のとりうる値の範囲を求めよ。$
$(解説)$
$(1)\ \ は差が正となることを示します。$
$(2)\ \ はx \rightarrow +0 \ \ と \ \ y'\ の符号を調べます。$
(1)
(i)$\ \ f(x)=\log (1+x) -(x-\cfrac{x^2}{2}) \quad とおくと \quad f'(x)=\cfrac{1}{1+x}-(1-x)=\cfrac{x^2}{1+x} > 0$
$したがって f(x)\ は単調増加となり \quad f(x) > f(0)=0$
$\quad \therefore \ x-\cfrac{x^2}{2} < \log (1+x) $
(ii)$\ \ g(x)=\cfrac{x}{\sqrt{1+x}}-\log (1+x) \quad とおくと$
\begin{eqnarray*} g'(x) &=&\cfrac{\sqrt{1+x}- x \times \cfrac{1}{2\sqrt{1+x}}}{1+x}- \cfrac{1}{1+x}\\ \\ &=&\cfrac{2+x}{2(1+x)\sqrt{1+x}}- \cfrac{1}{1+x}\\ \\ &=&\cfrac{2+x-2\sqrt{1+x}}{2(1+x)\sqrt{1+x}}\\ \\ &=&\cfrac{(\sqrt{1+x}-1)^2}{2(1+x)\sqrt{1+x}}\\ \\ &>&0\\ \end{eqnarray*} $したがって g(x) は単調増加となり g(x) > g(0)=0$
$\quad \therefore \log (1+x) < \cfrac{x}{\sqrt{1+x}}$
(i),(ii)$\ \ より \qquad x-\cfrac{x^2}{2} < \log (1+x) < \cfrac{x}{\sqrt{1+x}}$
(2)
$\quad y=\cfrac{1}{\log (1+x)}- \cfrac{1}{x} \quad について$
(i)
$\ \ (1)で示した \quad x-\cfrac{x^2}{2} < \log (1+x) < \cfrac{x}{\sqrt{1+x}} \quad において$
$\quad x-\cfrac{x^2}{2}=-\cfrac{x}{2}(x-2) \ \ は \ \ 0 < x < 2 \ \ で \ \ x-\cfrac{x^2}{2} > 0 \quad だから、それぞれの逆数をとると$
$\qquad \cfrac{1}{x-\dfrac{x^2}{2}} > \cfrac{1}{\log (1+x)} > \cfrac{\sqrt{1+x}}{x}$
$各辺から \cfrac{1}{x}\ \ を引いて$
$\qquad \cfrac{1}{x-\dfrac{x^2}{2}}-\cfrac{1}{x} > \cfrac{1}{\log (1+x)} -\cfrac{1}{x} > \cfrac{\sqrt{1+x}}{x}-\cfrac{1}{x}$
$左辺の関数を \ y_1\ とおくと$
$\quad y_1=\cfrac{1}{x-\dfrac{x^2}{2}}-\cfrac{1}{x}=\cfrac{1}{x(1-\dfrac{x}{2})}-\cfrac{1}{x}=\cfrac{1-(1-\dfrac{x}{2})}{x(1-\dfrac{x}{2})}=\cfrac{1}{2(1-\dfrac{x}{2})}$
$\quad x \longrightarrow +0 \quad のとき \quad y_1 \longrightarrow \cfrac{1}{2}$
$右辺の関数を \ y_2\ とおくと$
$\qquad y_2=\cfrac{\sqrt{1+x}}{x}-\cfrac{1}{x}=\cfrac{\sqrt{1+x}-1}{x}=\cfrac{1}{\sqrt{1+x}+1}$
$\qquad x \longrightarrow +0 \quad のとき \quad y_2 \longrightarrow \cfrac{1}{2}$
$はさみうちの原理より$
$\quad x \longrightarrow +0 \quad のとき \quad \cfrac{1}{\log (1+x)} -\cfrac{1}{x} \longrightarrow \cfrac{1}{2}$
(ii)
$\quad y'=\cfrac{-\dfrac{1}{1+x}}{\{\log (1+x)\}^2}+\cfrac{1}{x^2}=-\cfrac{1}{(1+x)\{\log (1+x)\}^2}+\cfrac{1}{x^2}=\cfrac{-x^2+(1+x)\{\log (1+x)\}^2}{x^2(1+x)\{\log (1+x)\}^2}$
$\quad (1)より \quad 0 < \log (1+x) < \cfrac{x}{\sqrt{1+x}} \quad だから \quad (1+x)\{\log (1+x)\}^2 < x^2$
$よって y' < 0 \ \ となり \ y\ は単調減少$
(iii)
$\quad y=\cfrac{x-\log (1+x)}{x\log (1+x)} \quad において \quad h(x)=x-\log (1+x) \quad とおくと$
$\quad h'(x)=1-\cfrac{1}{1+x}=\cfrac{x}{1+x} > 0 \quad だから \quad h(x)は単調増加となる。$
$\quad h(x) > h(0)=0 \quad よって \quad y > 0$
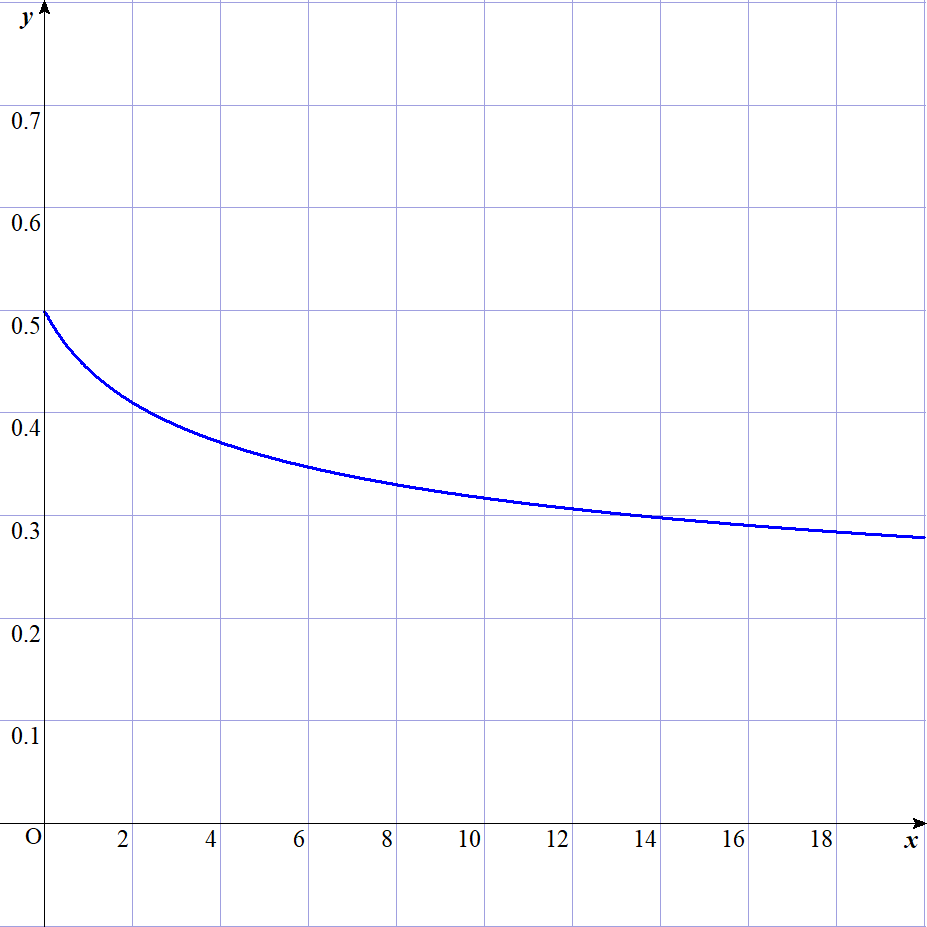
(i),(ii),(iii)$\ \ より \quad 0 < y < \cfrac{1}{2}$
$なお、グラフは右図のとおりです。$
メインメニュー に戻る