岡山大学(理系) 2024年 問題4
$座標平面上で、線分 \ S:x+y=1 \ \ (0 \leqq x \leqq 1) \ \ と曲線 \ C:\sqrt{x}+\sqrt{y}=1\ \ で囲まれた図形 \ D\ を考える。$
$S\ 上に点(0,\ 1)\ からの距離が \ t\ となる点 \ P\ をとる。このとき、0 \leqq t \leqq \sqrt{2}\ \ である。また、点 \ P\ を通り、$
$直線 \ x+y=1 \ と垂直に交わる直線を \ \ell \ とする。以下の問いに答えよ。$
$(1)\ \ 直線 \ \ell \ の方程式を \ t\ を用いて表せ。$
$(2)\ \ 直線 \ \ell \ と曲線 \ C\ の交点を \ Q\ とする。線分 \ PQ\ の長さを \ t\ を用いて表せ。$
$(3)\ \ 図形 \ D\ を直線 \ x+y=1\ のまわりに \ 1\ 回転してできる回転体の体積を求めよ。$
(1)
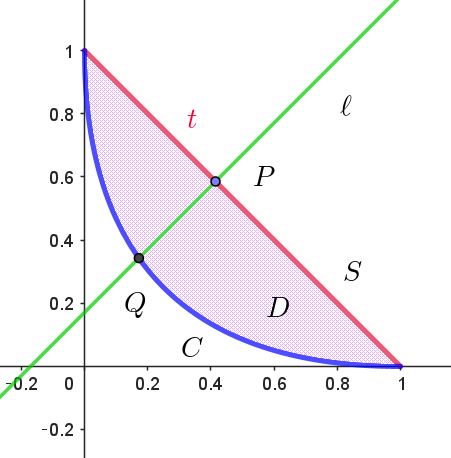
$曲線Cのグラフは右図のとおりで、通常の放物線を原点のまわりに$
$45°回転させたものです。$
$yについて解いて、微分すれば下に凸な単調減少であることがわかります。$
$P(p,\ q)\ \ とおくと$
$p=t\cos \dfrac{\pi}{4}=\cfrac{t}{\sqrt{2}}$
$q=1-t\sin \dfrac{\pi}{4}=1-\cfrac{t}{\sqrt{2}}$
$直線 \ \ell \ は線分 \ S\ に垂直だから 傾きは \ 1$
$y=(x-\cfrac{t}{\sqrt{2}})+1-\cfrac{t}{\sqrt{2}}$
$\ell : y=x+1-\sqrt{2}t$
(2)
$直線 \ \ell \ と曲線 \ C\ の交点\ Q\ は$
\[ \hspace{1em} \left\{ \begin{array}{l} y=x+1-\sqrt{2}t \hspace{5em}①\\ \sqrt{x}+\sqrt{y}=1 \hspace{6em}②\\ \end{array} \right. \]
$②より \quad \sqrt{y}=1-\sqrt{x} \qquad y=1-2\sqrt{x}+x$
$①を代入して \quad 2\sqrt{x}=1+x-y=1+x-(x+1-\sqrt{2}t)=\sqrt{2}t$
$\sqrt{x}=\cfrac{t}{\sqrt{2}} \qquad \therefore \ \ x=\cfrac{t^2}{2}$
$よって \quad y=\cfrac{t^2}{2}+1-\sqrt{2}t$
$Q(\cfrac{t^2}{2},\ \cfrac{t^2}{2}+1-\sqrt{2}t)$
$P(\cfrac{t}{\sqrt{2}}, \ 1-\cfrac{t}{\sqrt{2}}) \quad だから$
\begin{eqnarray*} PQ^2 &=&(\cfrac{t^2}{2}- \cfrac{t}{\sqrt{2}})^2+(\cfrac{t^2}{2}+1-\sqrt{2}t- (1-\cfrac{t}{\sqrt{2}}))^2\\ \\ &=&(\cfrac{t^2}{2}- \cfrac{t}{\sqrt{2}})^2+(\cfrac{t^2}{2} -\cfrac{t}{\sqrt{2}})^2\\ \\ &=&2(\cfrac{t^2}{2}- \cfrac{\sqrt{2}}{2}t)^2\\ \\ &=&\cfrac{t^2}{2}(t-\sqrt{2})^2\\ \end{eqnarray*} $0 \leqq t \leqq \sqrt{2} \quad だから \quad PQ=\cfrac{t}{\sqrt{2}}(\sqrt{2}-t)$
(3)
$回転体の体積 \ V\ は$
\begin{eqnarray*} V &=&\pi \int_0^{\sqrt{2}}PQ^2dt\\ \\ &=&\pi \int_0^{\sqrt{2}} \cfrac{t^2}{2}(\sqrt{2}-t)^2dt\\ \\ &=&\cfrac{\pi}{2} \int_0^{\sqrt{2}} (2t^2-2\sqrt{2}t^3+t^4)dt\\ \\ &=&\cfrac{\pi}{2} \big[\dfrac{2}{3}t^3-\dfrac{\sqrt{2}}{2}t^4+\dfrac{t^5}{5}\big]_0^{\sqrt{2}}\\ \\ &=&\cfrac{\pi}{2} \big(\dfrac{2}{3} \times 2\sqrt{2} -\dfrac{\sqrt{2}}{2} \times 4 +\dfrac{4\sqrt{2}}{5}\big)\\ \\ &=&\cfrac{\sqrt{2}}{15}\pi \end{eqnarray*}
$(補充)$
$この問題のように、回転軸が \ x\ 軸や \ y\ 軸でなく、一般の直線の場合は斜回転といいます。$
$斜回転による回転体の体積の求め方については、 この問題による方法の他$
斜回転による回転体の体積$をご覧ください。$
メインメニュー に戻る