岡山大学(理系) 2024年 問題3
$四面体 \ OABC \ において、OA=OB=OC=1\ \ とし、\angle COA=\alpha ,\ \ \angle COB=\beta ,\ \ \angle AOB=\gamma \ \ とする。$
$ただし、0 < \alpha < \dfrac{\pi}{2}, \ \ 0 < \beta < \dfrac{\pi}{2}\ \ とする。辺 \ OA\ の延長上に点 \ D\ を \ \vec{OC}\ と \ \vec{CD}\ が垂直になるようにとり、$
$辺 \ OB\ の延長上に点 \ E\ を \ \vec{OC}\ と \ \vec{CE}\ が垂直になるようにとる。\angle DCE=\theta \ \ とし、\vec{OA}=\vec{a},\ \ \vec{OB}=\vec{b},$
$\vec{OC}=\vec{c} \ \ とするとき、以下の問いに答えよ。$
$(1)\ \ \vec{CD}\ を \ \vec{a},\ \ \vec{c},\ \ \cos \alpha \ \ を用いて表せ。また、\vec{CE}\ \ を \ \vec{b},\ \ \vec{c},\ \ \cos \beta \ \ を用いて表せ。$
$(2)\ \ \cos \theta \ を \ \sin \alpha , \ \ \cos \alpha , \ \ \sin \beta , \ \ \cos \beta , \ \ \cos \gamma \ \ を用いて表せ。$
$(3)\ \ \cos \gamma =\cos \alpha \cos \beta , \ \ \beta =\dfrac{\pi}{2} - \alpha \ \ とする。点 \ C\ から平面 \ DOE\ に下ろした垂線の足を \ P\ とするとき、$
$\quad CP=\dfrac{1}{\tan \gamma} \ \ となることを示せ。$
(1)
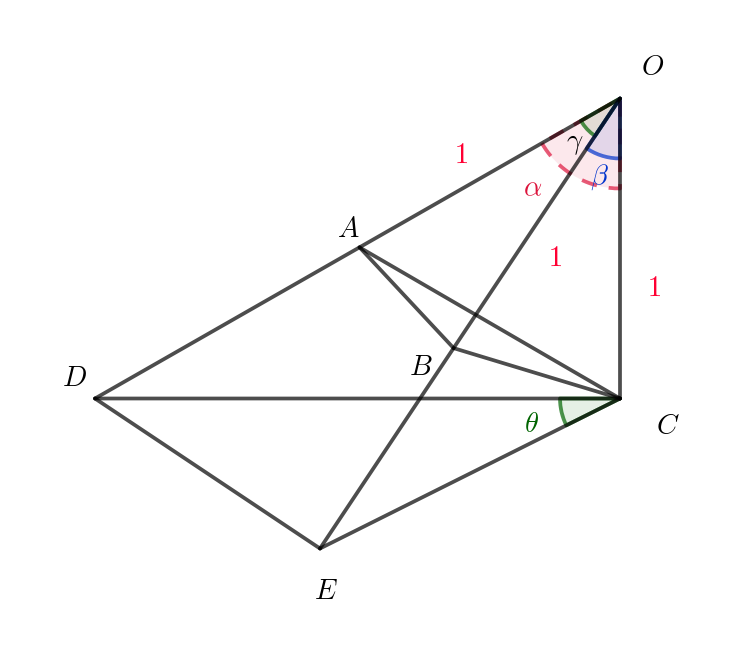
$直角三角形 \ OCD\ において \quad \cfrac{OC}{OD}=\cos \alpha $
$OD=\cfrac{OC}{\cos \alpha}=\cfrac{1}{\cos \alpha}$
$\vec{CD}=\vec{OD}-\vec{OC}=\cfrac{1}{\cos \alpha}\vec{OA}-\vec{OC}=\cfrac{1}{\cos \alpha}\vec{a}-\vec{c}$
$また、直角三角形 \ OCE\ において \quad \cfrac{OC}{OE}=\cos \beta $
$OE=\cfrac{OC}{\cos \beta}=\cfrac{1}{\cos \beta}$
$\vec{CE}=\vec{OE}-\vec{OC}=\cfrac{1}{\cos \beta}\vec{OB}-\vec{OC}=\cfrac{1}{\cos \beta}\vec{b}-\vec{c}$
(2)
$直角三角形 \ OCD\ において \quad \cfrac{CD}{OC}=\tan \alpha \qquad CD=OC \tan \alpha=\tan \alpha $
$直角三角形 \ OCE\ において \quad \cfrac{CE}{OC}=\tan \beta \qquad CE=OC \tan \beta=\tan \beta $
$(1)より$
$\vec{CD}\cdot \vec{CE}=\big(\cfrac{1}{\cos \alpha}\vec{a}-\vec{c}\big) \cdot \big(\cfrac{1}{\cos \beta}\vec{b}-\vec{c}\big)=\cfrac{1}{\cos \alpha \cos \beta }\vec{a}\cdot \vec{b} - \cfrac{1}{\cos \alpha}\vec{a}\cdot \vec{c} -\cfrac{1}{\cos \beta}\vec{b}\cdot \vec{c} +\vec{c}\cdot \vec{c}$
$ここで、\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cos \gamma=\cos \gamma, \qquad \vec{a}\cdot \vec{c}=|\vec{a}||\vec{c}|\cos \alpha=\cos \alpha ,\qquad \vec{b}\cdot \vec{c}=|\vec{b}||\vec{c}|\cos \beta=\cos \beta \quad だから$
$\vec{CD}\cdot \vec{CE}=\cfrac{\cos \gamma}{\cos \alpha \cos \beta } - \cfrac{\cos \alpha }{\cos \alpha} -\cfrac{\cos \beta }{\cos \beta} + 1=\cfrac{\cos \gamma}{\cos \alpha \cos \beta } - 1=\cfrac{\cos \gamma - \cos \alpha \cos \beta }{\cos \alpha \cos \beta } $
\begin{eqnarray*} \cos \theta &=&\cfrac{\vec{CD}\cdot \vec{CE}}{|\vec{CD}||\vec{CE}|}\\ \\ &=&\cfrac{\dfrac{\cos \gamma - \cos \alpha \cos \beta }{\cos \alpha \cos \beta }}{ \tan \alpha \tan \beta}\\ \\ &=&\cfrac{\cos \gamma - \cos \alpha \cos \beta }{\cos \alpha \cos \beta \tan \alpha \tan \beta}\\ \\ &=&\cfrac{\cos \gamma - \cos \alpha \cos \beta }{\sin \alpha \sin \beta } \end{eqnarray*}
$(別解)$
$\triangle ODE \ に余弦定理を用いて$
\begin{eqnarray*} DE^2 &=&OD^2+OE^2-2OD \cdot OE\cos \gamma\\ \\ &=&\cfrac{1}{\cos ^2 \alpha}+\cfrac{1}{\cos ^2 \beta}-2 \times \cfrac{1}{\cos \alpha} \times \cfrac{1}{\cos \beta} \times \cos \gamma\\ \\ &=&(1+\tan ^2 \alpha )+(1+\tan ^2 \beta )- \cfrac{2\cos \gamma}{\cos \alpha \cos \beta}\\ \\ &=&2+\tan ^2 \alpha +\tan ^2 \beta - \cfrac{2\cos \gamma}{\cos \alpha \cos \beta}\\ \end{eqnarray*}
$\triangle CDE \ に余弦定理を用いて$
\begin{eqnarray*} \cos \theta &=&\cfrac{CD^2+CE^2-DE^2}{2CD \cdot CE}\\ \\ &=&\cfrac{\tan ^2\alpha + \tan ^2\beta -\big(2+\tan ^2 \alpha +\tan ^2 \beta - \cfrac{2\cos \gamma}{\cos \alpha \cos \beta}\big)}{2\tan \alpha \tan \beta}\\ \\ &=&\cfrac{-2+ \cfrac{2\cos \gamma}{\cos \alpha \cos \beta}}{2\tan \alpha \tan \beta}\\ \\ &=&\cfrac{\cos \gamma -\cos \alpha \cos \beta }{\sin \alpha \sin \beta}\\ \end{eqnarray*}
(3)
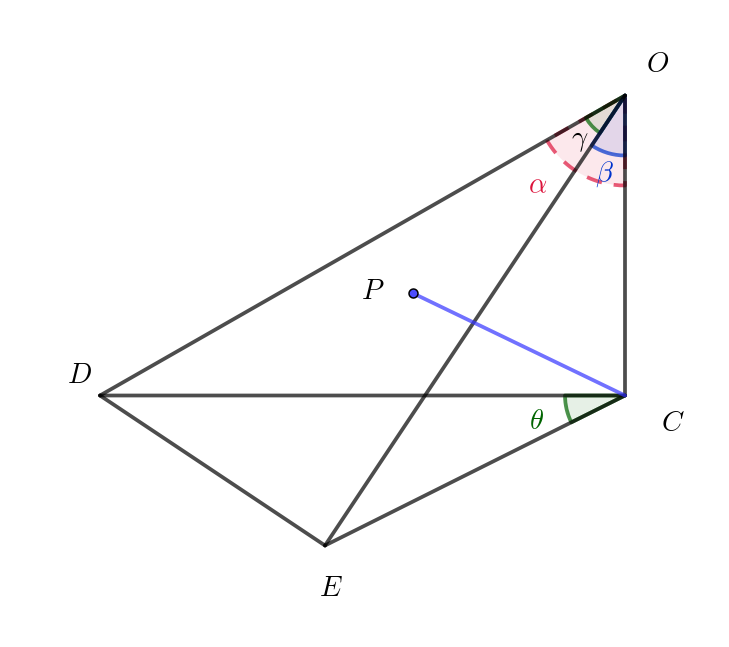
$線分OC\ は点 \ C\ で交わる \ 2\ 線分\ CD \ とCE\ に垂直だから、$
$OC \perp \triangle CDE$
$よって、四面体 \ OCDE\ の体積 \ V\ は$
\begin{eqnarray*}
V
&=&\cfrac{1}{3} \times \triangle CDE \times OC\\
\\
&=&\cfrac{1}{3} \times \cfrac{1}{2} \times CD \times CE \times \sin \theta \times 1\\
\\
&=&\cfrac{1}{6} \tan \alpha \tan \beta \sin \theta \\
\end{eqnarray*}
$また、線分 \ CP \perp \triangle DOE \quad だから$
\begin{eqnarray*}
V
&=&\cfrac{1}{3} \times \triangle DOE \times CP\\
\\
&=&\cfrac{1}{3} \times \cfrac{1}{2} \times OD \times OE \times \sin \gamma \times CP\\
\\
&=&\cfrac{\sin \gamma}{6\cos \alpha \cos \beta} \times CP\\
\end{eqnarray*}
$したがって$
$\cfrac{1}{6} \tan \alpha \tan \beta \sin \theta =\cfrac{\sin \gamma}{6\cos \alpha \cos \beta} \times CP$
$CP=\tan \alpha \tan \beta \sin \theta \times \cfrac{\cos \alpha \cos \beta}{\sin \gamma}=\cfrac{\sin \alpha \sin \beta \sin \theta }{\sin \gamma}$
$\cos \gamma =\cos \alpha \cos \beta \quad だから (2)より \quad \cos \theta=\cfrac{\cos \gamma -\cos \alpha \cos \beta }{\sin \alpha \sin \beta}=0 \qquad \therefore \ \ \theta=\cfrac{\pi}{2}$
$\beta =\dfrac{\pi}{2} - \alpha \quad だから \quad \sin \alpha=\sin (\dfrac{\pi}{2} - \beta)=\cos \beta ,\qquad \sin \beta=\sin (\dfrac{\pi}{2} - \alpha)=\cos \alpha$
$したがって$
$CP=\cfrac{\sin \alpha \sin \beta \sin \dfrac{\pi}{2}}{\sin \gamma}=\cfrac{\cos \beta \cos \alpha }{\sin \gamma}=\cfrac{\cos \gamma}{\sin \gamma}=\cfrac{1}{\tan \gamma}$
メインメニュー に戻る