岡山大学(理系) 2024年 問題2
$数直線上を動く点 \ P\ がある。点 \ P\ は、原点 \ O\ を出発して、1\ 枚のコインを \ 1\ 回投げるごとに、表が出たら$
$数直線上を正の向きに \ 1\ だけ進み、裏が出たら数直線上を負の向きに \ 1\ だけ進ものとする。コインの表が$
$出る確率と裏が出る確率はともに \ \dfrac{1}{2}\ であるとし、コインを \ n\ 回投げ終えた時点での点 \ P\ の座標を \ x_n \ とする。$
$コインを \ 10\ 回投げるとき、以下の問いに答えよ。$
$(1)\ \ x_{10}=0 \ \ となる確率を求めよ。$
$(2)\ \ x_5 \ne 1 \ \ かつ \ \ x_{10}=0 \ \ となる確率を求めよ。$
$(3)\ \ 0 \leqq x_n \leqq 3 \ \ (n=1,\ 2,\ \cdots ,\ 9)\ \ かつ \ \ x_{10} =0 \ \ となる確率を求めよ。$
(1)
$コインを \ 10\ 回投げて、表が \ k\ 回、裏が (10-k)\ 回出たときの点 \ P\ の座標は$
$x_{10}=k-(10-k)=2k-10 \quad だから$
$x_{10}=0 \ \ となるのは \quad 2k-10=0 \quad より \quad k=5$
$すなわち表が \ 5\ 回、裏が \ 5\ 回出るときだから、その確率は$
\begin{eqnarray*} P &=&{}_{10}C_5 \big(\dfrac{1}{2}\big)^5 \big(\dfrac{1}{2}\big)^5 \\ \\ &=&\cfrac{10 \times 9 \times 8 \times 7 \times 6}{5 \times 4 \times 3 \times 2} \times \cfrac{1}{2^{10}}\\ \\ &=&\cfrac{9 \times 7}{2^8}\\ \\ &=&\cfrac{63}{256} \end{eqnarray*}
(2)
$5\ 回目の試行で、表が \ k\ 回、裏が \ (5-k)\ 回 \ \ (k=0,1,2,3,4,5)\ \ 出る確率は \quad {}_5C_k \big(\dfrac{1}{2}\big)^k \times \big(\dfrac{1}{2}\big)^{5-k}={}_5C_k \big(\dfrac{1}{2}\big)^5$
$このとき、x_5=k-(5-k)=2k-5 \quad だから \quad x_{10}=0 \ \ となるには$
(i)$\ \ k=0 \ \ のとき \ \ x_5=-5 \ \ だから次の \ 5\ 回で表が \ 5\ 回、裏が \ 0\ 回出ればよい。$
$\quad p_0={}_5C_0 \big(\dfrac{1}{2}\big)^5 \times {}_5C_5 \big(\dfrac{1}{2}\big)^5=({}_5C_0)^2 \big(\dfrac{1}{2}\big)^{10}$
(ii)$\ \ k=1 \ \ のとき \ \ x_5=-3 \ \ だから次の \ 5\ 回で表が \ 4\ 回、裏が \ 1\ 回出ればよい。$
$\quad p_1={}_5C_1 \big(\dfrac{1}{2}\big)^5 \times {}_5C_4 \big(\dfrac{1}{2}\big)^5=({}_5C_1)^2 \big(\dfrac{1}{2}\big)^{10}$
(iii)$\ \ k=2 \ \ のとき \ \ x_5=-1 \ \ だから次の \ 5\ 回で表が \ 3\ 回、裏が \ 2\ 回出ればよい。$
$\quad p_2={}_5C_2 \big(\dfrac{1}{2}\big)^5 \times {}_5C_3 \big(\dfrac{1}{2}\big)^5=({}_5C_2)^2 \big(\dfrac{1}{2}\big)^{10}$
(iv)$\ \ k=3 \ \ のとき \ \ x_5=1 \ \ だから これは不適$
(v)$\ \ k=4 \ \ のとき \ \ x_5=3 \ \ だから次の \ 5\ 回で表が \ 1\ 回、裏が \ 4\ 回出ればよい。$
$\quad p_4={}_5C_4 \big(\dfrac{1}{2}\big)^5 \times {}_5C_1 \big(\dfrac{1}{2}\big)^5=({}_5C_4)^2 \big(\dfrac{1}{2}\big)^{10}$
(vi)$\ \ k=5 \ \ のとき \ \ x_5=5 \ \ だから次の \ 5\ 回で表が \ 0\ 回、裏が \ 5\ 回出ればよい。$
$\quad p_5={}_5C_5 \big(\dfrac{1}{2}\big)^5 \times {}_5C_0 \big(\dfrac{1}{2}\big)^5=({}_5C_5)^2\big(\dfrac{1}{2}\big)^{10}$
$よって求める確率は$
\begin{eqnarray*} P &=&p_0+p_1+p_2+p_4+p_5\\ \\ &=&(({}_5C_0)^2 +({}_5C_1)^2 + ({}_5C_2)^2 +({}_5C_4)^2 +({}_5C_5)^2 )\big(\dfrac{1}{2}\big)^{10}\\ \\ &=&(1^2 + 5^2 + 10^2 + 5^2 + 1^2 )\big(\dfrac{1}{2}\big)^{10}\\ \\ &=&152 \times \big(\dfrac{1}{2}\big)^{10}\\ \\ &=&\cfrac{19}{128} \end{eqnarray*}
$(別解)$
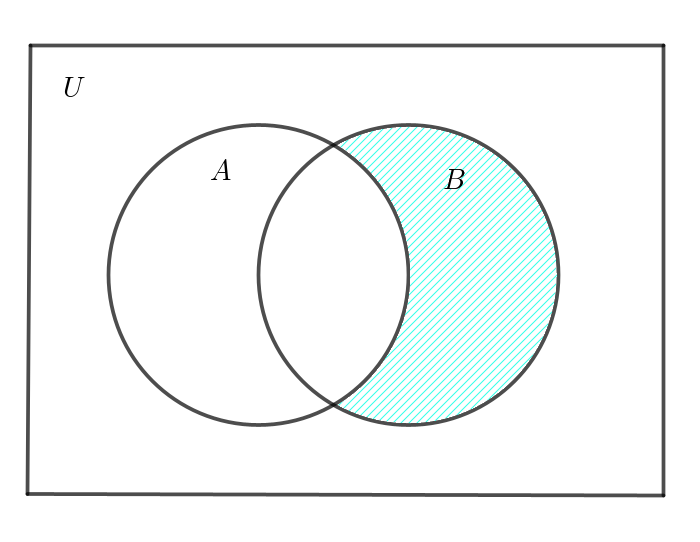
$コインを \ 10\ 回投げたときの各回ごとの表裏の状態を全事象 \ U\ として$
$とくに、x_5=1 \ である事象を \ A,\ \ x_{10}=0 \ \ である事象を \ B\ とする。$
$x_5 \ne 1 \ \ かつ \ \ x_{10}=0 \ \ となる事象は \ \ \overline{A} \cap B $
$P(\overline{A} \cap B)=P(B)-P(A \cap B)=P(B)-P(A)P_A(B)$
$P(A)\ は初めの \ 5\ 回で表が \ 3\ 回、裏が \ 2\ 回出る確率だから$
$P(A)={}_{5}C_3 \big(\dfrac{1}{2}\big)^3 \big(\dfrac{1}{2}\big)^2={}_{5}C_3 \big(\dfrac{1}{2}\big)^5$
$P_A(B)\ \ は事象 \ A\ が起きたとき事象 \ B\ が起こる条件付き確率だから$
$x_5=1\ \ として \ \ x_{10}=0 \ \ となる事象は次の \ 5\ 回で表が \ 2\ 回、裏が \ 3\ 回出ればよい。$
$P_A(B)={}_{5}C_2 \big(\dfrac{1}{2}\big)^2 \big(\dfrac{1}{2}\big)^3={}_{5}C_2 \big(\dfrac{1}{2}\big)^5$
$よって$
\begin{eqnarray*}
P(\overline{A} \cap B)
&=&P(B)-P(A)P_A(B)\\
\\
&=&{}_{10}C_5 \big(\dfrac{1}{2}\big)^{10}-{}_{5}C_3 \big(\dfrac{1}{2}\big)^5 \times {}_{5}C_2 \big(\dfrac{1}{2}\big)^5\\
\\
&=&\big({}_{10}C_5 - {}_{5}C_3 \times {}_{5}C_2 \big) \times \cfrac{1}{2^{10}}\\
\\
&=&\big(\cfrac{10 \times 9 \times 8 \times 7 \times 6}{5 \times 4 \times 3 \times 2} - \cfrac{5 \times 4 \times 3 }{3 \times 2} \times \cfrac{5 \times 4 }{2}\big) \times \cfrac{1}{2^{10}} \\
\\
&=&(252-10 \times 10 ) \times \cfrac{1}{2^{10}} \\
\\
&=&\cfrac{19}{128}
\end{eqnarray*}
(3)
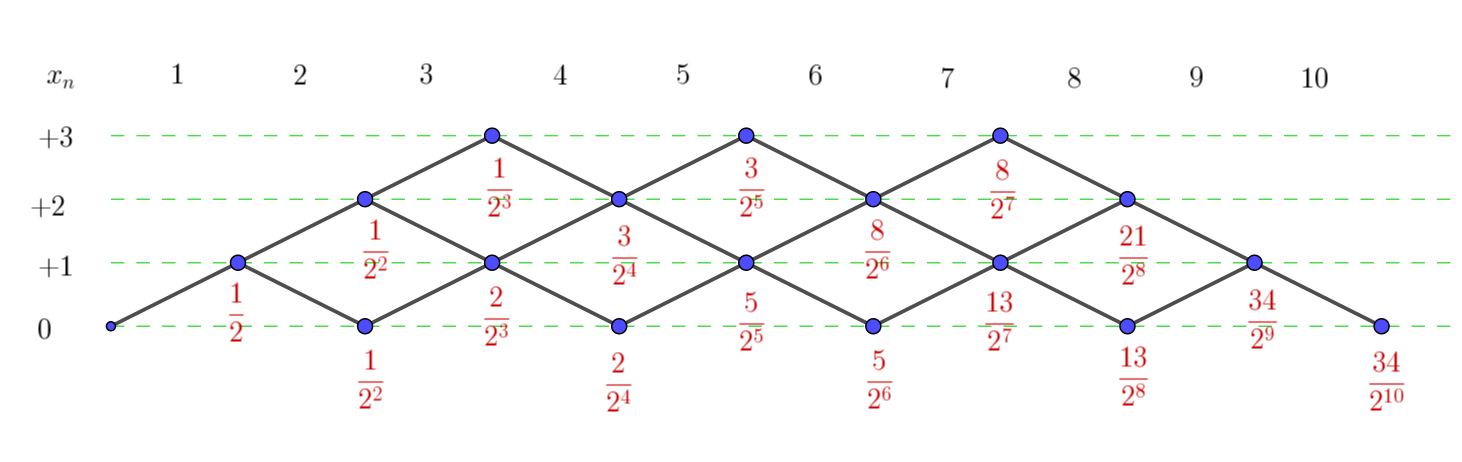
$上図は、コインを投げて表が出れば右上に進み、裏が出れば右下に進む樹形図で、$
$0 \leqq x_n \leqq 3 \ \ (n=1,\ 2,\ \cdots ,\ 9)\ \ かつ \ \ x_{10} =0 \ \ となる事象を表わしている。$
$例えば、表が出ることを \ H、裏が出ることを \ T\ と表すと$
$3\ 回投げて$
(i)$\ \ x_3=3 \ \ となるのは、H\ H\ H\ の \ 1\ 通りであるからこの事象の確率は \ \ \cfrac{1}{2^3}$
(ii)$\ \ x_3=1 \ \ となるのは、H\ H\ T\ \ と \ H\ T\ H\ \ の \ 2\ 通りであるからこの事象の確率は \ \ \cfrac{2}{2^3}$
$4\ 回投げて$
$x_4=2\ \ となるのは、$(i)$\ \ に続いて \ T\ である場合と$(ii)$に続いて \ H\ の場合があるから$
$この事象の確率は \quad \cfrac{1}{2^3} \times \cfrac{1}{2} + \cfrac{2}{2^3} \times \cfrac{1}{2} =\cfrac{3}{2^4}$
$このようにして、各回ごとに樹形図に確率を付けて、10\ 回投げたとき条件を満たす事象の確率を求めると$
$P=\cfrac{34}{2^{10}}=\cfrac{17}{2^9}=\cfrac{17}{512}$
メインメニュー に戻る