お茶の水女子大学(数学専門) 2025年　問題2


$x > 0\ \ とする。f(x)=x\log \dfrac{1}{x} \ \ とし、a_1=\dfrac{1}{2}\ \ とする。xy\ 平面において、関数 \ y=f(x)\ \ のグラフ上の$
$点(a_1,\ f(a_1))\ \ における法線と \ x\ 軸との交点の \ x\ 座標を \ a_2 \ とする。同様に \ n=2,\ 3,\ 4,\ \cdots \ \ に対して、$
$点(a_n,\ f(a_n))\ \ における \ y=f(x)\ の法線とx軸との交点の \ x\ 座標を \ \ a_{n+1}\ とする。$
$また、g(x)=x+f(x)f'(x) \ \ と定める。以下の問いに答えよ。$
$ただし、必要であれば \ \ e > 2 \ \ を証明なしに用いてもよい。$
$(1)\ \ g'(x)=0 \ \ となる \ x\ を求めよ。$
$(2)\ \ x > \dfrac{1}{e} \ \ のとき、g(x) > \dfrac{1}{e}\ \ が成り立つことを示せ。$
$(3)\ \ n=1,\ 2,\ 3,\ \cdots \ \ に対して、a_{n+1}=g(a_n) \ \ であることを示し、\dfrac{1}{e} < a_{n+1} < a_n \ \ が成り立つことを示せ。$
$(4)\ \ \dfrac{1}{e}< x \leqq \dfrac{1}{2}\ \ のとき、-e < \dfrac{f'(x)}{x- \dfrac{1}{e}} < -2 \ \ が成り立つことを示せ。$
\[(5)\ \ \big|a_{n+1} - \dfrac{1}{e} \big| \leqq (1-\log 2)\big|a_n-\dfrac{1}{e} \big| \ \ が成り立つことを示し、極限 \ \ \lim_{n \rightarrow \infty} a_n \ \ を求めよ。\]


(1)


$f(x)=x\log \dfrac{1}{x}=-x\log x \quad より \quad f'(x)=-\log x -1=-(1+\log x)$

$f'(x)=0 \quad より \quad \log x=-1 \qquad x=\dfrac{1}{e}$

　

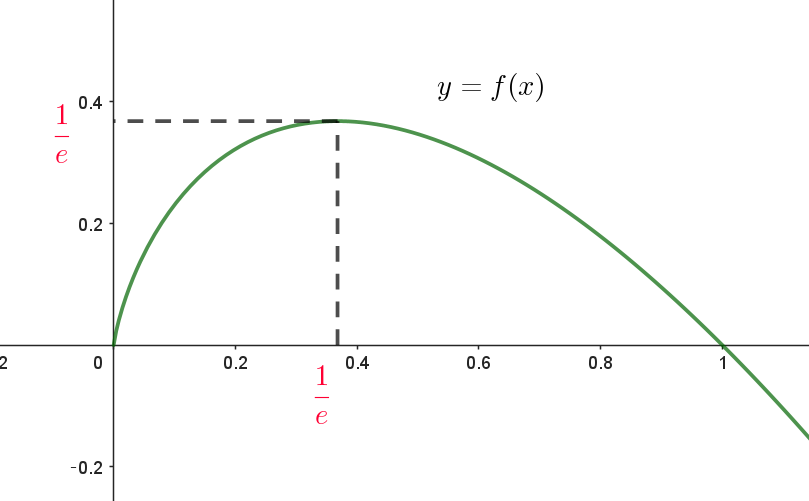
\[ \begin{array}{c||c|c|c|c|c} x& 0 & \cdots & \dfrac{1}{e} & \cdots \\ \hline f'(x)& & + & 0 & - \\ \hline f(x)& & \nearrow & 極大 & \searrow \\ \end{array} \]
$x=\cfrac{1}{e}\ でf(x)\ は極大かつ最大となり、最大値は$

$f(\dfrac{1}{e})=\dfrac{1}{e}\log e=\dfrac{1}{e}$

$y=f(x) \ のグラフは右図のとおり$

$g(x)=x+f(x)f'(x) =x+(-x\log x)\big(-(1+\log x)\big)=x\big(1+\log x + (\log x)^2\big)$
\begin{eqnarray*} g'(x) &=&\big(1+\log x +(\log x)^2 \big)+ x\big(\dfrac{1}{x}+2\log x \times \dfrac{1}{x}\big)\\ \\ &=&(\log x)^2+3\log x+2\\ \\ &=&(1+\log x)(2+\log x) \end{eqnarray*}
$g'(x)=0 \quad より \quad \log x=-1 ,\quad \log x=-2 \qquad \therefore \ \ x=\dfrac{1}{e},\quad \dfrac{1}{e^2}$


(2)

　

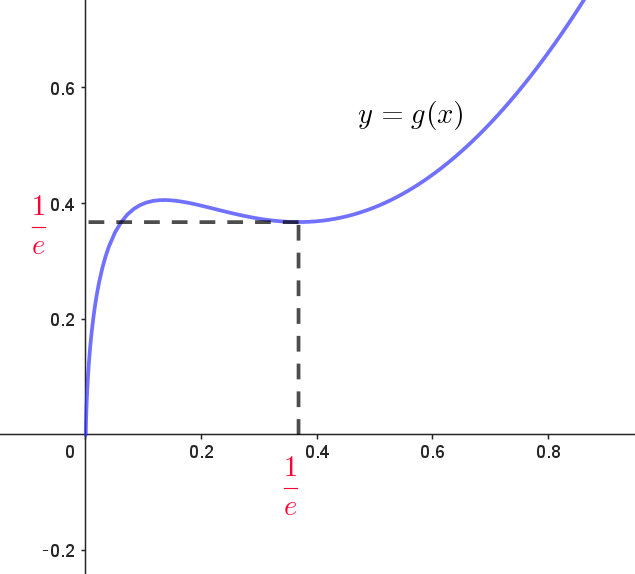
$x > \dfrac{1}{e} \ \ のとき、\log x >-1 \quad だから \quad g'(x) >0$

$よって\ \ g(x)\ はこの区間で単調増加$

$g(\dfrac{1}{e})=\dfrac{1}{e}\big(1+\log \dfrac{1}{e}+(\log \dfrac{1}{e})^2\big)=\dfrac{1}{e}\big(1-1+ (-1)^2\big)=\dfrac{1}{e} \quad だから$

$x > \dfrac{1}{e} \quad のとき \quad g(x) > g(\dfrac{1}{e})=\dfrac{1}{e}$


(3)

　

$点(a_n,\ f(a_n))\ \ における \ \ y=f(x)\ \ の法線は$

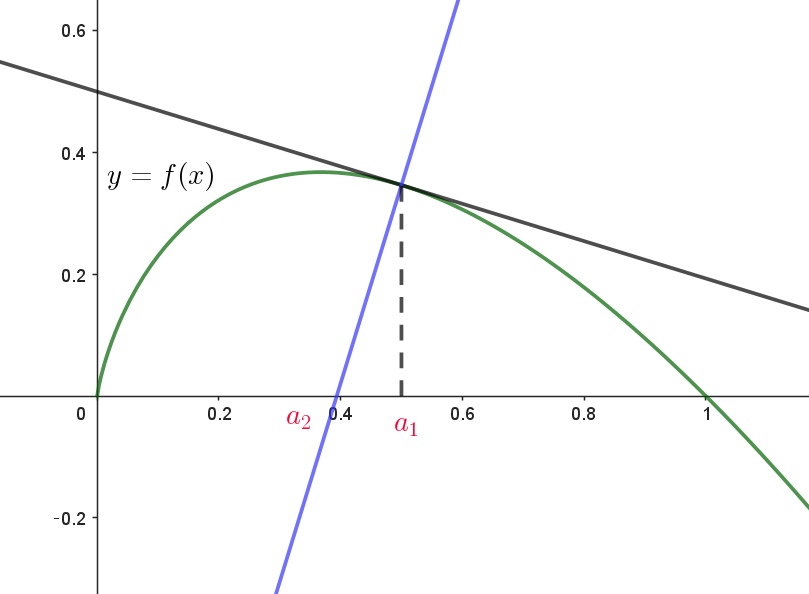
$f'(x)=-(1+\log x) \quad だから \quad y=\dfrac{1}{1+\log a_n}(x-a_n)+f(a_n)$

$x\ 軸との交点の \ x\ 座標が \ \ a_{n+1}\ \ だから$

$0=\dfrac{1}{1+\log a_n}(a_{n+1}-a_n)-a_n\log a_n$

$a_{n+1}-a_n=(1+\log a_n)a_n\log a_n$

$a_{n+1}=a_n(1+ \log a_n+ (\log a_n)^2)$

$(1)より \quad g(x)=x\big(1+\log x + (\log x)^2\big) \quad だから \quad a_{n+1}=g(a_n)$

$(2)より \ g(x)\ は単調増加で、g(\dfrac{1}{e})=\dfrac{1}{e},\quad g(1)=1 $

$e > 2 \quad だから \quad a_1=\dfrac{1}{2} > \dfrac{1}{e}$

$一般に、\dfrac{1}{e}< a_k < 1 \quad とすると \quad g(\dfrac{1}{e}) < g(a_k) < g(1) \quad \therefore\ \ \dfrac{1}{e} < a_{k+1} < 1$

$数学的帰納法により 任意の自然数 \ n\ に対して \quad \dfrac{1}{e} < a_n < 1 $

$このとき \quad -1 < \log a_n < 0 \quad だから \quad 1+\log a_n >0$

$a_{n+1}-a_n=(1+\log a_n)a_n\log a_n <0 $

$よって \quad 　\dfrac{1}{e} < a_{n+1} < a_n$


(4)


$(3)より \quad 　a_{n+1} < a_n \quad だから$

$ a_n < a_{n-1} < \cdots < a_1=\dfrac{1}{2} $

$よって　\dfrac{1}{e} < a_n < \dfrac{1}{2} $

$\dfrac{1}{e} < x \leqq \dfrac{1}{2} \quad として　区間 \ \ \big[\dfrac{1}{e},\ x\big]\ \ を考える。$

$f(x)=x\log \dfrac{1}{x}=-x\log x \quad より \quad f'(x)=-(1+\log x) \quad はこの区間で連続で、微分可能だから$

$平均値の定理を用いて \quad \dfrac{f'(x)-f'(\dfrac{1}{e})}{x-\dfrac{1}{e}}=f''(c) \quad (\dfrac{1}{e} < c < x \leqq \dfrac{1}{2}) \ \ をみたす実数 \ c\ が存在する。$

$f'(\dfrac{1}{e})=-1+\log e=0 ,\quad f''(x)=-\dfrac{1}{x}\quad より \quad f''(c)=-\dfrac{1}{c}$

$\dfrac{1}{e} < c < \dfrac{1}{2}\quad より \quad 2 < \dfrac{1}{c} < e \qquad -e < -\dfrac{1}{c} < -2$

$よって \quad 　-e < f''(c) < -2$

$したがって \quad -e < \dfrac{f'(x)}{x-\dfrac{1}{e}} < -2$


(5)


$(4)より \quad -e(x-\dfrac{1}{e}) < f'(x) < -2(x-\dfrac{1}{e})$

$g(x)=x+f(x)f'(x) \quad より \quad f'(x)=\dfrac{g(x)-x}{f(x)}$

$よって \quad -e(x-\dfrac{1}{e}) < \dfrac{g(x)-x}{f(x)} < -2(x-\dfrac{1}{e})$

$x=a_n \ \ (\dfrac{1}{e} < a_n < \dfrac{1}{2})\ \ とおくと \quad -e(a_n-\dfrac{1}{e}) < \dfrac{g(a_n)-a_n}{f(a_n)} <-2(a_n-\dfrac{1}{e})$

$f(a_n)=-a_n\log a_n > 0 \quad だから分母をはらって$

$a_n-e(a_n-\dfrac{1}{e})f(a_n) < g(a_n) < a_n -2(a_n-\dfrac{1}{e})f(a_n)$

$a_n-\dfrac{1}{e}-e(a_n-\dfrac{1}{e})f(a_n) < g(a_n)-\dfrac{1}{e} < a_n-\dfrac{1}{e}-2(a_n-\dfrac{1}{e})f(a_n)$

$(a_n-\dfrac{1}{e})(1-ef(a_n)) < g(a_n)-\dfrac{1}{e} < (a_n-\dfrac{1}{e})(1-2f(a_n))$

$\therefore \ \ 1-ef(a_n) < \cfrac{a_{n+1}-\dfrac{1}{e}}{a_n-\dfrac{1}{e}} < 1-2f(a_n)$

$(1) でかいた \ y=f(x)\ のグラフからわかるとおり$

$f(\dfrac{1}{e})=\dfrac{1}{e},\qquad f(\dfrac{1}{2})=\dfrac{1}{2}\log 2 \quad だから$

$\dfrac{1}{e} < a_n < \dfrac{1}{2} \quad のとき \quad \dfrac{1}{2}\log 2 < f(a_n) < \dfrac{1}{e} $

$1-2f(a_n) < 1-2 \times \dfrac{1}{2}\log 2=1-\log 2$

$ 0 < 1-ef(a_n) < 1-2f(a_n) \quad だから$

$\big|\cfrac{a_{n+1}-\dfrac{1}{e}}{a_n-\dfrac{1}{e}} \big| < 1-2f(a_n)<1-\log 2$

$\therefore \ \ \big|a_{n+1}-\dfrac{1}{e}\big| \leqq (1-\log 2) \big|{a_n-\dfrac{1}{e}} \big| $

$よって$
\begin{eqnarray*} & &\big|a_n-\dfrac{1}{e}\big|\\ \\ &\leqq& (1-\log 2) \big|{a_{n-1}-\dfrac{1}{e}} \big|\\ \\ &\leqq& (1-\log 2)^2 \big|{a_{n-2}-\dfrac{1}{e}} \big|\\ \\ & &\hspace{3em} \vdots \\ \\ &\leqq& (1-\log 2)^{n-1} \big|{a_1-\dfrac{1}{e}} \big|\\ \\ &\leqq& (1-\log 2)^{n-1} \big|{\dfrac{1}{2}-\dfrac{1}{e}} \big|\\ \end{eqnarray*} $0 < 1-\log 2 < 1 \quad だから \quad n \longrightarrow \infty \quad のとき \quad (1-\log 2)^{n-1} \longrightarrow 0$

\[0 < \big|a_n-\dfrac{1}{e}\big| \quad だからはさみうちの原理により \quad \lim_{n \rightarrow \infty} a_n=\dfrac{1}{e}\]

ページの先頭へ↑




メインメニュー　に戻る