新潟大学(理系) 2025年　問題6


$座標平面上の曲線y=x\sin ^2x をCとする。自然数nに対して、曲線C上に点P_n(n\pi,o),点Q_n(\dfrac{2n-1}{2}\pi,\dfrac{2n-1}{2}\pi) をとる。$
$次の問いに答えよ。$
$(1)\ \ 曲線C上の点P_nにおける接線の方程式を求めよ。また、曲線C上の点Q_nにおける接線の方程式を求めよ。$
$(2)\ \ 曲線C と線分P_nP_{n+1} で囲まれた部分の面積S_n をnを用いて表せ。$
$(3)\ \ 曲線C と線分Q_nQ_{n+1} で囲まれた部分の面積T_n をnを用いて表せ。$
\[(4)\ \ S_n とT_n は(2)と(3)で求めたものとする。極限値 \lim_{k \rightarrow \infty} \dfrac{\sum_{n=1}^k S_n}{\sum_{n=1}^k T_n} を求めよ。\]


(1)

　

$曲線 \ C\ のグラフは、\sin ^2x \ のグラフを \ y\ 軸方向に \ x\ 倍$

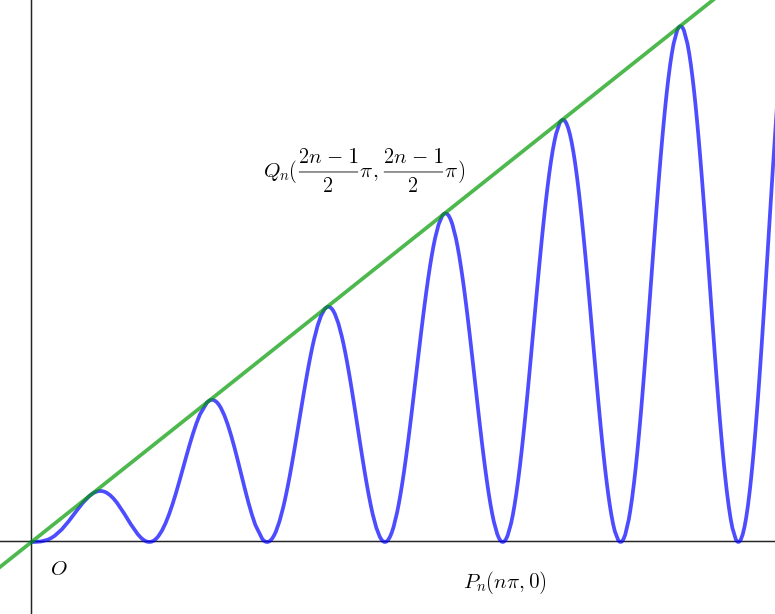
$したもので、x\ 軸と \ y=x \ に挟まれている。$

$\sin x=0 \ の点は \ x\ 軸上に、\sin x=1\ の点は \ y=x \ 上にある。$

$y=x\sin ^2x \ \ より$

$y'=\sin ^2x + 2x\sin x \cos x=\sin ^2x + x\sin 2x$

(i)$\ \ 点P_n\ における接線は$

$\quad y'=\sin ^2 n\pi + n\pi \sin 2n\pi=0 \ \ だから \quad y=0$

(ii)$\ \ 点Q_n\ における接線は$

$\quad y'=\sin ^2 \dfrac{2n-1}{2}\pi + \dfrac{2n-1}{2}\pi \sin (2n-1)\pi=1 \ \ だから$

$\quad y=(x-\dfrac{2n-1}{2}\pi)+\dfrac{2n-1}{2}\pi \qquad \therefore \ \ y=x$


(2)

　

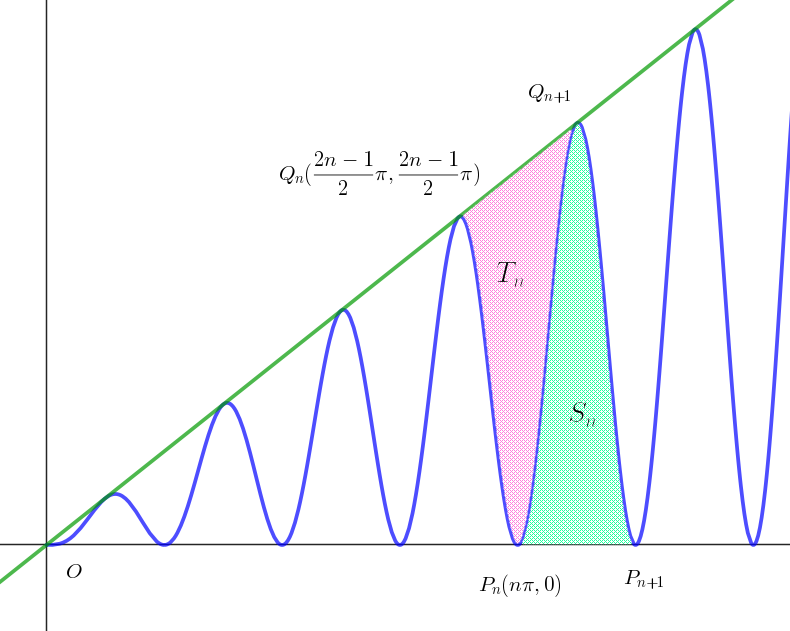
\begin{eqnarray*} S_n &=&\int_{n\pi}^{(n+1)\pi} x\sin ^2xdx\\ \\ &=&\cfrac{1}{2}\int_{n\pi}^{(n+1)\pi} x(1-\cos 2x)dx\\ \\ &=&\cfrac{1}{2}\int_{n\pi}^{(n+1)\pi} xdx -\cfrac{1}{2}\int_{n\pi}^{(n+1)\pi} x\cos 2xdx\\ \\ &=&\cfrac{1}{4}\big[x^2\big]_{n\pi}^{(n+1)\pi}-\cfrac{1}{4}\big[x\sin 2x\big]_{n\pi}^{(n+1)\pi} + \cfrac{1}{4}\int_{n\pi}^{(n+1)\pi} \sin 2xdx\\ \\ &=&\cfrac{1}{4}\big\{(n+1)^2\pi ^2-n^2 \pi ^2 \big\} -\cfrac{1}{4}\big\{(n+1)\pi \sin2(n+1)\pi -n\pi \sin 2n\pi\big\} -\\ \\ & & \qquad \cfrac{1}{8}\big[\cos 2x \big]_{n\pi}^{(n+1)\pi} \\ \\ &=&\cfrac{1}{4}(2n+1)\pi ^2 - \cfrac{1}{8}\big\{ \cos 2(n+1)\pi -\cos 2n\pi\big\}\\ \\ &=&\cfrac{2n+1}{4}\pi ^2 \end{eqnarray*}

(3)


\begin{eqnarray*} T_n &=&\int_{\scriptsize{\dfrac{2n-1}{2}\pi}}^{\scriptsize{\dfrac{2n+1}{2}\pi}} (x-x\sin ^2x)dx\\ \\ &=&\int_{\scriptsize{\dfrac{2n-1}{2}\pi}}^{\scriptsize{\dfrac{2n+1}{2}\pi}} x\cos ^2xdx\\ \\ &=&\cfrac{1}{2}\int_{\scriptsize{\dfrac{2n-1}{2}\pi}}^{\scriptsize{\dfrac{2n+1}{2}\pi}} x(1+\cos 2x)dx\\ \\ &=&\cfrac{1}{2}\int_{\scriptsize{\dfrac{2n-1}{2}\pi}}^{\scriptsize{\dfrac{2n+1}{2}\pi}} xdx + + \cfrac{1}{2}\int_{\scriptsize{\dfrac{2n-1}{2}\pi}}^{\scriptsize{\dfrac{2n+1}{2}\pi}} x\cos 2xdx\\ \\ &=&\cfrac{1}{4}\big[x^2 \big]_{\scriptsize{\dfrac{2n-1}{2}\pi}}^{\scriptsize{\dfrac{2n+1}{2}\pi}} + \cfrac{1}{4}\big[ x\sin 2x\big]_{\scriptsize{\dfrac{2n-1}{2}\pi}}^{\scriptsize{\dfrac{2n+1}{2}\pi}}- \cfrac{1}{4}\int_{\scriptsize{\dfrac{2n-1}{2}\pi}}^{\scriptsize{\dfrac{2n+1}{2}\pi}} \sin 2x dx\\ \\ &=&\cfrac{1}{4}\big\{(\dfrac{2n+1}{2})^2\pi ^2 -(\dfrac{2n-1}{2})^2\pi ^2\big\} + \cfrac{1}{4}\big\{ \dfrac{2n+1}{2}\pi \sin (2n+1)\pi - \dfrac{2n-1}{2}\pi \sin(2n-1)\pi\big\} + \cfrac{1}{8}\big[\cos 2x \big]_{\scriptsize{\dfrac{2n-1}{2}\pi}}^{\scriptsize{\dfrac{2n+1}{2}\pi}} \\ \\ &=&\cfrac{1}{4} \times 2n \pi ^2 + \cfrac{1}{8}\big\{\cos (2n+1)\pi - \cos (2n-1)\pi \big\}\\ \\ &=&\cfrac{n}{2}\pi ^2 \end{eqnarray*}

(4)


\begin{eqnarray*} & &\cfrac{\sum_{n=1}^k S_n}{\sum_{n=1}^k T_n}\\ \\ &=&\cfrac{\sum_{n=1}^k \dfrac{2n+1}{4}\pi ^2}{\sum_{n=1}^k \dfrac{n}{2}\pi^2}\\ \\ &=&\cfrac{1}{2} \times \cfrac{2 \times \dfrac{k(k+1)}{2} +k}{\dfrac{k(k+1)}{2}}\\ \\ &=&\cfrac{k(k+2)}{k(k+1)}\\ \\ &=&\cfrac{1 +\dfrac{2}{k}}{1+\dfrac{1}{k}}\\ \end{eqnarray*} \[よって \quad \lim_{k \rightarrow \infty} \dfrac{\sum_{n=1}^k S_n}{\sum_{n=1}^k T_n}=1\]

ページの先頭へ↑




メインメニュー　に戻る