新潟大学(理系) 2025年　問題5


$次の条件(☆)を満たす複素数 \ z\ を考える。ただし、i\ は虚数単位とする。$
$(☆)\ iz^2 \ は実数であって、0 \leqq iz^2 \leqq 2 \ \ である。$
$次の問いに答えよ。$
$(1)\ \ iz^2=2 \ \ であるときの複素数 \ z\ をすべて求めよ。$
$(2)\ \ 0 < iz^2 \leqq 2 \ \ であるときの複素数 \ z\ の偏角 \ \theta \ をすべて求めよ。ただし、0 \leqq \theta < 2\pi \ \ とする。$
$(3)\ \ 条件(☆)を満たす複素数 \ z\ 全体の集合を \ S\ とする。集合 \ S\ を複素数平面上に図示せよ。$
$(4)\ \ 複素数 \ z\ が(3)の \ S\ を動くとき、\dfrac{z}{z+2} \ \ の実部の最小値を求めよ。$


(1)


$z=a+bi\ \ (a,\ b \ は実数)\ \ とおくと$

$iz^2=2 \ \ より \quad i(a+bi)^2=2$

$i(a^2-b^2+2abi)=2$

$-2ab +(a^2-b^2)i=2$
\[ \hspace{1em} \left\{ \begin{array}{l} -2ab=2 \hspace{6em}①\\ a^2-b^2=0 \hspace{5em}②\\ \end{array} \right. \]
$②より \quad b=\pm a \quad これを①に代入して$

(i)$\ \ b=a \ \ のとき \quad a^2=-1 \quad これは不適$

(ii)$\ \ b=-a \ \ のとき \quad a^2=1 \qquad a=\pm1 、よって \qquad b=\mp 1$

$したがって \quad z=1-i,\ \ -1+i$


$(別解)$

$iz^2=2 \ \ より \quad z^2=\cfrac{2}{i}=-2i=2(\cos \dfrac{3}{2}\pi + i \sin \dfrac{3}{2}\pi)$

$z=r(\cos \theta + i\sin \theta) \ \ とおくと \quad z^2=r^2(\cos 2\theta + i\sin 2\theta) \ \ だから$

$r^2=2 \quad \therefore\ \ r=\sqrt{2}$

$0 \leqq \theta < 2\pi \ \ で考えると \quad 0 \leqq 2\theta < 4\pi \ \ だから$

(i)$\ \ 2\theta=\cfrac{3}{2}\pi \ \ のとき \quad \theta=\cfrac{3}{4}\pi \ \ だから$

$\quad z=\sqrt{2}(\cos \dfrac{3}{4} + i\sin \dfrac{3}{4}\pi)=-1+i$

(ii)$\ \ 2\theta=\cfrac{7}{2}\pi \ \ のとき \quad \theta=\cfrac{7}{4}\pi \ \ だから$

$\quad z=\sqrt{2}(\cos \dfrac{7}{4} + i\sin \dfrac{7}{4}\pi)=1-i$


(2)


$0 < iz^2 \leqq 2 \ \ より \ \ iz^2 \ \ は正の実数、したがって偏角は \ \ \theta=2k\pi \ \ (k\ は正の整数)\ \ とおける。$

$\theta = \arg (z) \ \ と表すことにすると \qquad \arg(iz^2)=2k\pi$

$偏角の性質から \quad \arg(i)+2\arg(z)=2k\pi$

$\cfrac{\pi}{2}+2\theta=2k\pi \qquad \therefore \ \ \theta=(k-\dfrac{1}{4})\pi$

$0 \leqq \theta < 2\pi \ \ より$

(i)$\ \ k=1 \ \ のとき \quad \theta=\cfrac{3}{4}\pi$

(ii)$\ \ k=2 \ \ のとき \quad \theta=\cfrac{7}{4}\pi$


(3)

　

$z=0 \ \ のとき \quad iz^2=0 \ \ だから \quad 0 \in S$

$z \ne 0 \ \ のとき$

$z\ の偏角 \ \theta \ \ について$

$(2)より \quad \theta=\cfrac{3}{4}\pi, \ \ \cfrac{7}{4}\pi$

$z\ の絶対値について$

$0 < |iz^2| \leqq 2 \ \ より \quad 0 < |z|^2 \leqq 2 \qquad \therefore \ \ 0 < |z| \leqq \sqrt{2}$

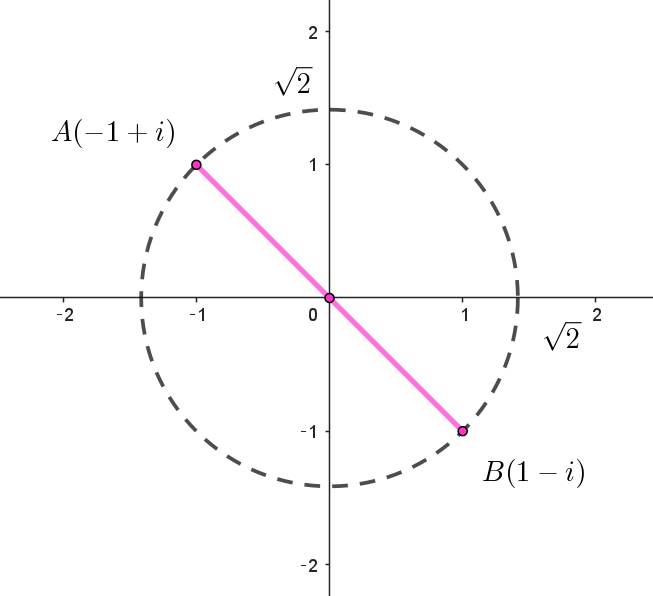
$したがって \quad z=r(\cos \dfrac{3}{4}\pi+i \sin \dfrac{3}{4}\pi), \quad z=r(\cos \dfrac{7}{4}\pi+i \sin \dfrac{7}{4}\pi) \quad ただし \quad 0 < r \leqq \sqrt{2}$

$集合 \ S\ は右図のとおり$


(4)


$(3)の \ S\ は \ \ z=t-ti \ \ (-1 \leqq t \leqq 1) \ \ とおけるから$

\begin{eqnarray*} \dfrac{z}{z+2} &=&\cfrac{t-ti}{(t-ti)+2}\\ \\ &=&\cfrac{t-ti}{(t+2)-ti}\\ \\ &=&\cfrac{(t-ti)\{(t+2)+ti\}}{(t+2)^2+t^2}\\ \\ &=&\cfrac{(t(t+2)+t^2+ \{t^2-t(t+2)\}i}{(t+2)^2+t^2}\\ \\ &=&\cfrac{2t^2 + 2t -2ti}{(t+2)^2+t^2}\\ \end{eqnarray*} $これの実部を \ f(t)\ \ (-1 \leqq t \leqq 1)\ \ とおくと$

$f(t)=\cfrac{2(t^2 + t) }{(t+2)^2+t^2}=\cfrac{t^2 + t }{t^2+2t +2}$

$f'(t)=\cfrac{(2t + 1)(t^2+2t+2)-(t^2+t)(2t+2)}{(t^2+2t+2)^2}=\cfrac{t^2+4t+2}{(t^2+2t+2)^2}$

$f'(t)=0 \ \ より \quad t^2+4t+2=0 $

$-1 \leqq t \leqq 1 \ \ だから \quad t=-2 + \sqrt{2}$

\[ \begin{array}{c||c|c|c|c|c} t& -1 & \cdots & -2+\sqrt{2} & \cdots & 1\\ \hline f'(t)& & - & 0 & + & \\ \hline f(t)& & \searrow & 極小 & \nearrow & \\ \end{array} \] $f(t)\ は \ \ t=-2+\sqrt{2}\ \ で極小かつ最小となり、最小値は$

$t=-2+\sqrt{2} \ \ のとき \ \ t^2=-4t-2 \ \ だから$

　

\begin{eqnarray*} f(t) &=&\cfrac{t^2 + t }{t^2+2t +2}\\ \\ &=&\cfrac{(-4t-2)+t}{(-4t-2)+2t+2}\\ \\ &=&\cfrac{3t+2}{2t}\\ \\ &=&\cfrac{3}{2}+\cfrac{1}{t} \end{eqnarray*} $と簡単にして代入すると$

$f(-2+\sqrt{2})=\cfrac{3}{2}+\cfrac{1}{-2+\sqrt{2}}=\cfrac{3}{2}-\cfrac{2+\sqrt{2}}{2}=\cfrac{1-\sqrt{2}}{2}$

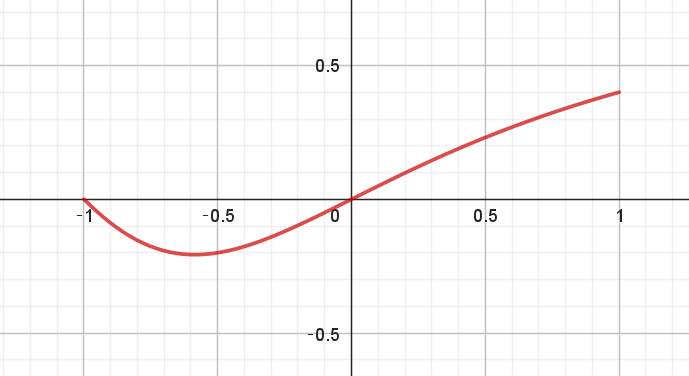
$なお、f(t) \ のグラフは右図のとおりです。$


ページの先頭へ↑




メインメニュー　に戻る