新潟大学(理系) 2025年　問題4


$2\ つの関数 \ f(x)=~\log _2 x,\ \ g(x)=|x^2-2x-3|-|x^2-x|\ \ について、それらの合成関数$
$f(x)=(g \circ f)(x)=g(f(x)) \ \ を考える。次の問いに答えよ。$
$(1)\ \ \dfrac{1}{16} \leqq x \leqq 4 \ \ のとき、\ \ f(x)\ のとりうる値の範囲を求めよ。$
$(2)\ \ \dfrac{1}{16} \leqq x \leqq 4 \ \ のとき、h(x)\ のとりうる値の範囲を求めよ。$
$(3)\ \ 関数 \ y=h(x)\ \ (\dfrac{1}{16} \leqq x \leqq 4 )\ \ のグラフと直線 \ y=1\ の共有点の個数を求めよ。また、共有点の \ x\ 座標を$
$\quad すべて求めよ。$
$(4)\ \ a\ は定数とする。関数 \ y=h(x) \ \ (\dfrac{1}{16} \leqq x \leqq 4 )\ \ のグラフと直線 \ y=a \ が共有点をもつとき、その共有点$
$\quad の個数を \ a\ の値によって場合分けして求めよ。$


　

(1)


$\dfrac{1}{16} \leqq x \leqq 4 \ \ より \quad 2^{-4} \leqq x \leqq 2^2 $

$\log _2 2^{-4} \leqq \log _2 x \leqq \log_2 2^2 $

$\therefore \ \ -4 \leqq f(x) \leqq 2$

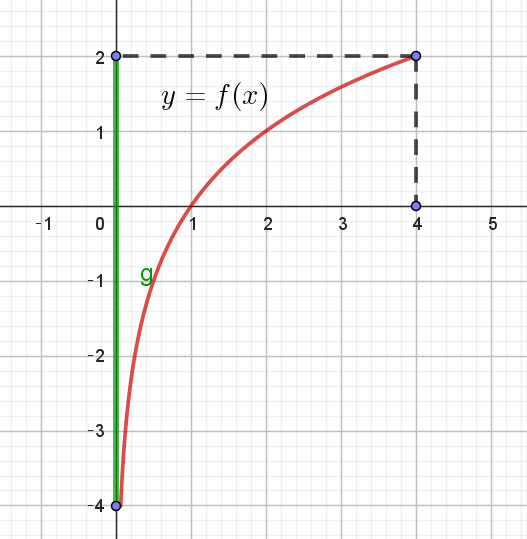
$なお、y=f(x)\ のグラフは右図のとおり$


(2)


$f(x)=\log _2 x=u \ \ とおくと \ (1)より \ \ -4 \leqq u \leqq 2$

$h(x)=g(f(x))\ \ に対して \ \ h^*(u)=g(u)\ \ とおくと$

$u\ は \ x\ の単調増加関数で、1\ 対 \ 1\ 対応であるから、$

$h(x)\ と \ h^*(u)\ の増減は対応する。$

　

$g(u)=|u^2-2u-3|-|u^2-u|=|(u+1)(u-3)|-|u(u-1)|$

(i)$\ \ -4 \leqq u \leqq -1 \ \ のとき$

$\quad g(u)=(u^2-2u-3)-(u^2-u)=-u-3$

(ii)$\ \ -1 \leqq u \leqq 0 \ \ のとき$
\begin{eqnarray*} \quad g(u) &=&-(u^2-2u-3)-(u^2-u)\\ \\ &=&-2u^2+3u+3\\ \\ &=&-2(u-\dfrac{3}{4})^2+\dfrac{33}{8} \end{eqnarray*} (iii)$\ \ 0 \leqq u \leqq 1 \ \ のとき$

$\quad g(u)=-(u^2-2u-3)+(u^2-u)=u+3$

(iv)$\ \ 1 \leqq u \leqq 2 \ \ のとき$

$\quad g(u)=-(u^2-2u-3)-(u^2-u)=-2u^2+3u+3$

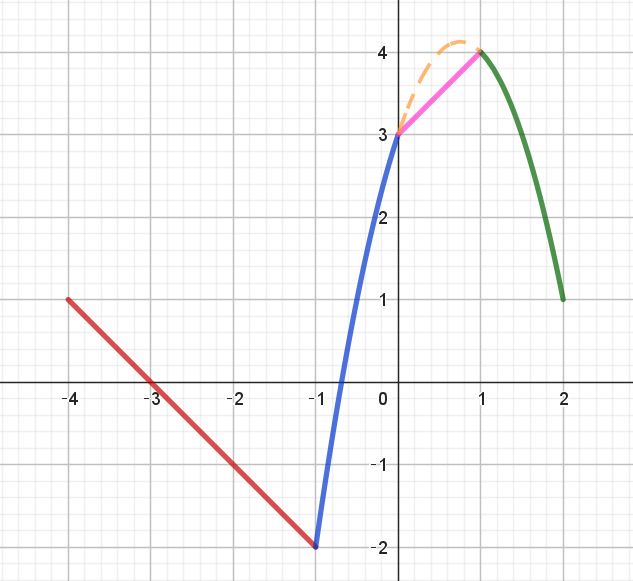
$h^*(u)=g(u) のグラフは右図のとおりで、-2 \leqq g(u) \leqq 4$

$h(x)\ のとりうる値の範囲も -2 \leqq h(x) \leqq 4$


(3)

　

$y=h^*(u) \ と \ y=1\ の共有点は$

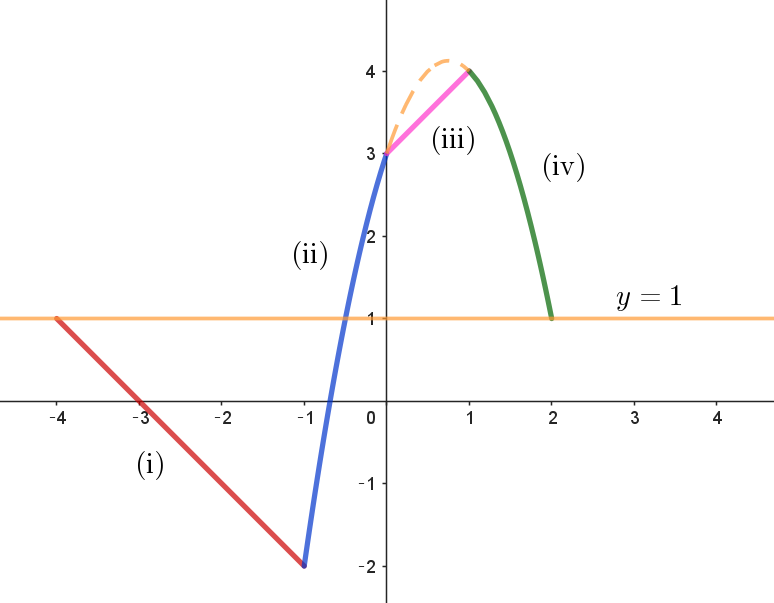
(i)$との交点が\ \ u=-4$

(ii)$との交点が \ \ -2u^2+3u+3=1\ \ を解いて \ \ 2u^2-3u-2=0$

$\quad (2u+1)(u-2)=0 \quad -1 \leqq u \leqq 0 \ \ だから \ \ u=-\cfrac{1}{2}$

(iv)$との交点が\ \ u=2$

$したがって 共有点の個数は \ 3\ 個で、\log_2 x=u \ \ より \ \ x=2^u \ \ だから $

$u=-4 \ \ のとき \quad x=2^{-4}=\cfrac{1}{16}$

$u=-\cfrac{1}{2} \ \ のとき \quad x=2^{-\scriptsize{\dfrac{1}{2}}}=\cfrac{1}{\sqrt{2}}$

$u=2 \ \ のとき \quad x=2^2=4$


(4)

　

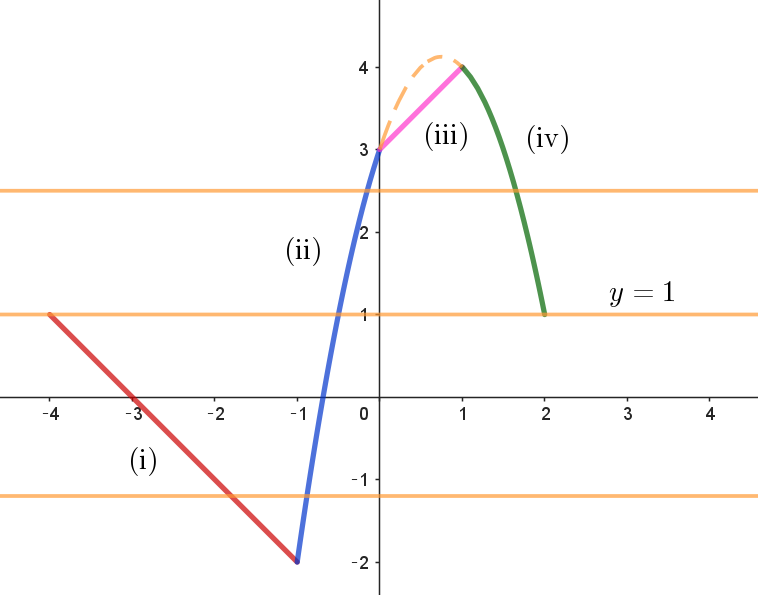
$y=h(x) \ \ (\dfrac{1}{16} \leqq x \leqq 4 )\ \ のグラフと直線 \ y=a \ の共有点の個数は$

$y=h^*(u) \ \ (-4 \leqq u \leqq 2 )\ \ のグラフと直線 \ y=a \ の共有点の$

$個数に一致するから$

$\quad a=-2 \ \ のとき \hspace{4em} 1\ 個$

$\quad -2 < a < 1 \ \ のとき \hspace{2.5em} 2\ 個$

$\quad a=1 \ \ のとき \hspace{5em} 3\ 個$

$\quad 1 < a < 4 \ \ のとき \hspace{3.5em} 2\ 個$

$\quad a=4 \ \ のとき \hspace{5em} 1\ 個$
\begin{eqnarray*} \end{eqnarray*}


ページの先頭へ↑




メインメニュー　に戻る