新潟大学(理系) 2025年　問題1


$座標平面上の原点を\ O\ とし、1\ 点 \ A(a,\ -1)\ をとる。ただし、a > 0\ とする。また、放物線 \ y=x^2 \ 上に点 \ B$
$をとる。ただし、B\ は原点以外の点とする。次の問いに答えよ。$
$(1)\ \ ベクトル \ \vec{OA},\ \ \vec{OB}\ が垂直になるときの点 \ B\ の座標を \ a\ を用いて表せ。また、そのときの三角形 \ OAB\ の$
$\quad 面積 \ S\ を \ a\ を用いて表せ。$ $(2)\ \ 内積 \ \vec{OA}\cdot \vec{OB}\ が最大になるときの点 \ B\ の座標を \ a\ を用いて表せ。また、そのときの三角形 \ OAB\ の面積$
$\quad T\ を \ a\ を用いて表せ。$ $(3)\ \ S\ と \ T\ は、(1)と(2)で求めたものとする。S=3T\ \ となるときの点 \ A\ の座標を求めよ。$


(1)

　

$B(b,\ b^2) \quad とおく。$

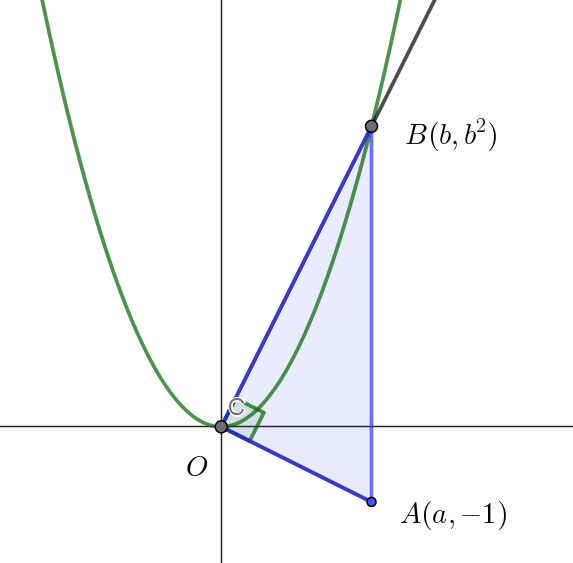
$\vec{OA} \perp \vec{OB} \quad だから \quad \vec{OA} \cdot \vec{OB}=0$

$(a,\ -1) \cdot (b,\ b^2)=0$

$ab-b^2=0 \qquad b(a-b)=0$

$b \ne 0 \quad だから \quad b=a \qquad よって \ \ B(a,\ a^2)$

\begin{eqnarray*} S &=&\triangle OAB\\ \\ &=&\cfrac{1}{2} \times OA \times OB\\ \\ &=&\cfrac{1}{2} \times \sqrt{a^2+1} \times \sqrt{a^2+a^4}\\ \\ &=&\cfrac{1}{2} \times \sqrt{a^2+1} \times a \sqrt{1+a^2}\\ \\ &=&\cfrac{1}{2} a(a^2+1) \end{eqnarray*}

(2)


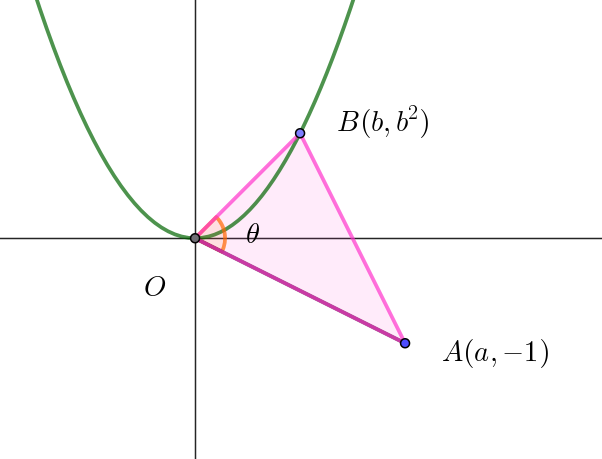
\begin{eqnarray*} \vec{OA}\cdot \vec{OB} &=&(a,\ -1) \cdot (b,\ b^2)\\ \\ &=&ab-b^2\\ \\ &=&-(b^2-ab)\\ \\ &=&-(b-\dfrac{a}{2})^2+\dfrac{a^2}{4} \end{eqnarray*}
$b=\dfrac{a}{2} \ \ のとき最大値 \ \ \dfrac{a^2}{4}\ \ をとる。$

$このとき \quad B(\dfrac{a}{2},\ \dfrac{a^2}{4})$

　

\begin{eqnarray*} T &=&\triangle OAB\\ \\ &=&\cfrac{1}{2} \times OA \times OB \times \sin \theta\\ \\ &=&\cfrac{1}{2} \times OA \times OB \times \sqrt{1-\cos ^2 \theta}\\ \\ &=&\cfrac{1}{2} \times OA \times OB \times \sqrt{1-\big(\dfrac{\vec{OA}\cdot \vec{OB}}{|\vec{OA}||\vec{OB}|}\big)^2}\\ \\ &=&\cfrac{1}{2} \sqrt{|\vec{OA}|^2|\vec{OB}|^2 -(\vec{OA}\cdot \vec{OB})^2}\\ \\ &=&\cfrac{1}{2} \sqrt{(a^2+1)(\dfrac{a^2}{4} + \dfrac{a^4}{16})-(\dfrac{a^2}{2}-\dfrac{a^2}{4})^2}\\ \\ &=&\cfrac{1}{2} \sqrt{\dfrac{a^2}{16}(a^2+1)(4+a^2)-\dfrac{a^4}{16}}\\ \\ &=&\cfrac{a}{8} \sqrt{(a^2+1)(a^2+4)-a^2}\\ \\ &=&\cfrac{a}{8} \sqrt{a^4+4a^2+4}\\ \\ &=&\cfrac{a}{8}(a^2+2) \end{eqnarray*}

(3)


$S=3T \ \ より$

$\cfrac{1}{2} a(a^2+1)=3 \times \cfrac{a}{8}(a^2+2)$

$4a(a^2+1)=3a(a^2+2)$

$a^3-2a=0$

$a(a^2-2)=0$

$a > 0 \quad だから \quad a=\sqrt{2}$

$よって \quad A(\sqrt{2},\ -1)$


ページの先頭へ↑




メインメニュー　に戻る