新潟大学(理系) 2024年 問題6
$実数 \ t\ に対して、複素数 \ z\ を次の条件(Ⅰ),(Ⅱ)を満たすようにとる。$
$\qquad (Ⅰ) \ z\ の虚部は \ 0\ 以上である。$
$\qquad (Ⅱ) \ z^2-2t^3z+t^6+9t^2=0$
$この \ z\ に対して、複素数 \ w\ を \ w=i \overline{z} \ とおく。ただし、i\ は虚数単位とし、\overline{z}\ は \ z\ の共役複素数とする。$
$次の問いに答えよ。$
$(1)\ \ 複素数 \ z\ と \ w\ を \ t\ を用いて表せ。$
$(2)\ \ 0 \leqq t \leqq 2 \ のとき、|z-w|\ の最大値を求めよ。また、そのときの \ t\ の値をすべて求めよ。$
$(3)\ \ 実数 \ t\ を動かしたとき、複素数平面上で \ z\ が表す点が描く曲線を \ C_1\ とし、w\ が表す点が描く曲線を$
$\quad C_2\ とする。C_1\ と \ C_2\ で囲まれる図形の面積を求めよ。$
(1)
$z^2-2t^3z+t^6+9t^2=0 \quad より$
\begin{eqnarray*} z &=&t^3 \pm \sqrt{t^6-(t^6+9t^2)}\\ \\ &=&t^3 \pm \sqrt{-9t^2}\\ \\ &=&t^3 \pm 3ti \end{eqnarray*}
$z\ の虚部は \ 0\ 以上だから$
(i)$\ \ t \geqq 0 \quad のとき$
$\quad z=t^3 + 3ti \quad で \quad w=i(t^3 -3ti)=3t+t^3i$
(ii)$\ \ t < 0 \quad のとき$
$\quad z=t^3 - 3ti \quad で \quad w=i(t^3 +3ti)=-3t+t^3i$
(2)
$0 \leqq t \leqq 2 \ \ のとき \quad z=t^3 + 3ti ,\quad w=3t+t^3i$
\begin{eqnarray*} |z-w| &=&|(t^3 + 3ti)-(3t+t^3i)|\\ \\ &=&|t^3-3t -(t^3-3t)i|\\ \\ &=&|t^3-3t||1 -i|\\ \\ &=&\sqrt{2}|t^3-3t|\\ \end{eqnarray*}
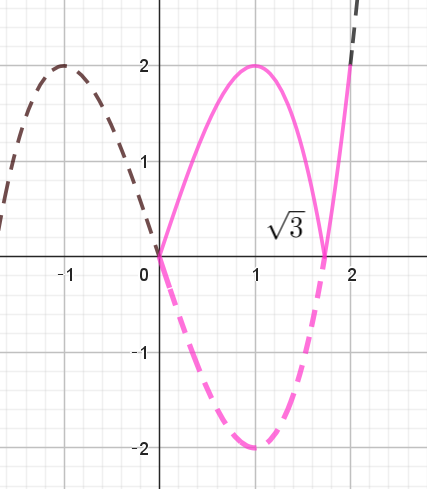
$f(t)=t^3-3t=t(t^2-3)\ \ のグラフは \ t\ 軸と \ t=0,\ \ \pm \sqrt{3}\ \ で交わることに注意して絶対値をはずすと$
\[ |z-w|= \hspace{1em} \left\{ \begin{array}{l} \sqrt{2}(3t-t^3) \hspace{5em} (0 \leqq t \leqq \sqrt{3})\\ \sqrt{2}(t^3-3t) \hspace{5em} (\sqrt{3} < t \leqq 2) \\ \end{array} \right. \]
$g(t)=3t-t^3 \quad の増減は$
$g'(t)=3-3t^2=-3(t+1)(t-1) \quad より$
$増減表$
\[
\begin{array}{c||c|c|c|c|c}
t& 0 & \cdots & 1 & \cdots &\sqrt{3} \\
\hline
g'(t)& & + & 0 & - & \\
\hline
g(t)& & \nearrow & 極大 & \searrow & \\
\end{array}
\]
$t=1\ で \ g(t)\ は極大かつ最大となり、最大値は \ \ g(1)=2$
$f(t)=t^3-3t \ \ は \ \ \sqrt{3} \leqq t \leqq 2 \ \ で単調増加だから \ t=2\ で最大値 \ \ f(2)=2\ \ をとる。$
$グラフをかくと右図のとおりである。$
$よって、|z-w|\ \ は \ \ t=1,\ 2\ \ のとき最大値 \ 2\sqrt{2}\ をとる。$
(3)
$(1)より$
(i)$\ \ t < 0 \quad のとき$
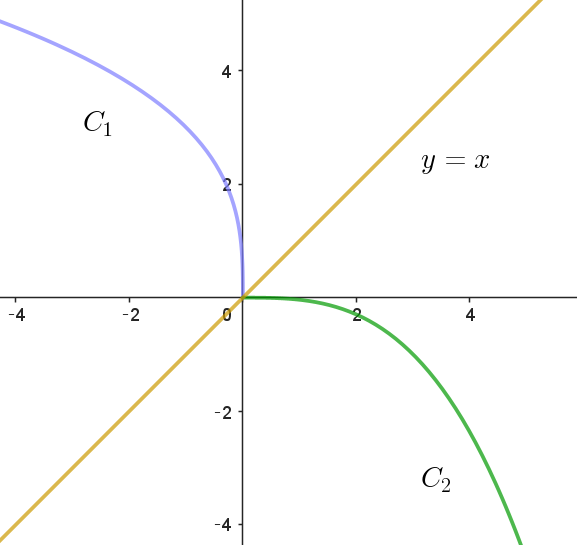
$\quad z=t^3 - 3ti \quad だから \quad x=t^3,\quad y=-3t \quad とおくと $
$\quad x=\big(-\dfrac{y}{3}\big)^3 \qquad C_1:x=-\cfrac{y^3}{27} \ \ (y > 0)$
$\quad w=-3t+t^3i \quad だから \quad x=-3t, \quad y=t^3 \quad とおくと$
$\quad y=\big(-\dfrac{x}{3}\big)^3 \qquad C_2:y=-\cfrac{x^3}{27} \ \ (x > 0)$
$C_1\ と \ C_2\ のグラフは右図のとおりで、囲まれない。$
(ii)$\ \ t \geqq 0 \quad のとき$
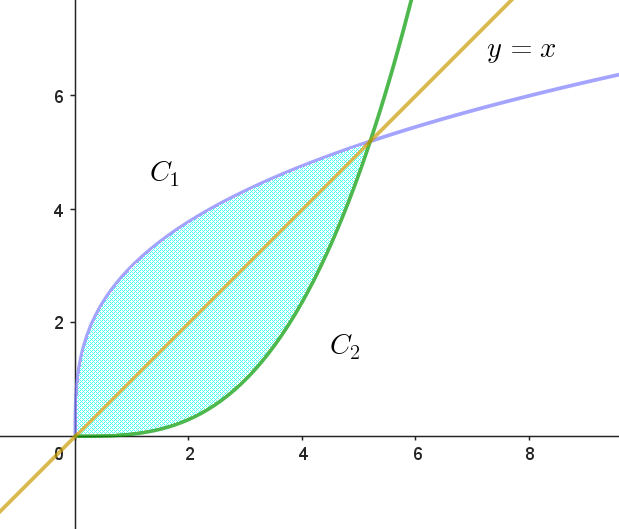
$\quad z=t^3 + 3ti \quad だから \quad x=t^3,\quad y=3t \quad とおくと $
$\quad x=\big(\dfrac{y}{3}\big)^3 \qquad C_1:x=\cfrac{y^3}{27}\ \ ( y \geqq 0)$
$\quad w=3t+t^3i \quad だから \quad x=3t, \quad y=t^3 \quad とおくと$
$\quad y=\big(\dfrac{x}{3}\big)^3 \qquad C_2:y=\cfrac{x^3}{27}\ \ (x \geqq 0)$
$C_1\ と \ C_2\ のグラフは右図のとおりである。$
$C_1\ と \ C_2\ で囲まれる図形の面積を \ S\ とすると$
$C_1\ と \ C_2\ は直線 \ y=x \ に関して対称だから$
$交点は \quad \cfrac{x^3}{27}=x \quad を解いて \quad x=0,\ \ 3\sqrt{3}$
\begin{eqnarray*}
S
&=&2\int_0^{3\sqrt{3}}\big(x-\dfrac{x^3}{27}\big)dx\\
\\
&=&2\big[\dfrac{x^2}{2}-\dfrac{x^4}{4 \times 27}\big]_0^{3\sqrt{3}}\\
\\
&=&2\big(\dfrac{27}{2}-\dfrac{27^2}{4 \times 27}\big)\\
\\
&=&\cfrac{27}{2}
\end{eqnarray*}
メインメニュー に戻る