新潟大学(理系) 2024年 問題5
$a\ を \ 0 < a < 1\ となる実数とする。座標平面上において、長さが \ 4\ の線分 \ PQ\ を考える。線分 \ PQ\ の端点 \ P\ は$
$x\ 軸上を、端点 \ Q\ は \ y\ 軸上を動くとき、線分 \ PQ\ を \ a:(1-a)\ の比に内分する点 \ R\ の軌跡は楕円になる。$
$この楕円を \ C\ とする。ただし、円は楕円の特別な場合とする。次の問いに答えよ。$
$(1)\ \ 楕円 \ C\ の方程式を \ a\ を用いて表せ。$
$(2)\ \ 楕円 \ C\ で囲まれた部分と連立不等式$
\[\qquad
\hspace{1em}
\left\{ \begin{array}{l}
x \geqq 0\\
\sqrt{3}ax \geqq (1-a)y\\
\end{array} \right.
\]
$\quad の表す領域の共通部分の面積を \ S\ とする。S\ を \ a\ を用いて表せ。$
$(3)\ \ 面積 \ S\ の最大値とそのときの \ a\ の値を求めよ。$
(1)
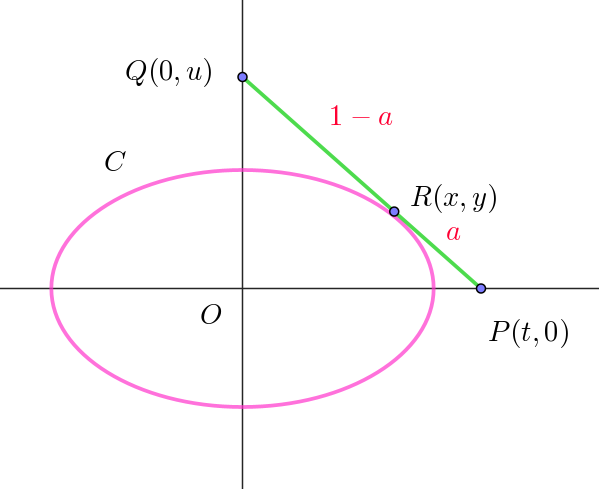
$P(t,\ 0),\ \ Q(0,\ u)\ とおくと \ R(x,\ y)\ は線分 \ PQ\ を$
$a:(1-a)\ の比に内分する点だから$
$x=(1-a)t,\qquad y=au$
$\therefore \ \ t=\cfrac{x}{1-a},\qquad u=\cfrac{y}{a}$
$PQ=4 \quad より \quad PQ^2=16 \qquad t^2+u^2=16$
$よって \quad \big(\cfrac{x}{1-a}\big)^2+\big(\cfrac{y}{a}\big)^2=16$
$\cfrac{x^2}{16(1-a)^2}+ \cfrac{y^2}{16a^2}=1$
$これが楕円 \ C\ の方程式である。$
(2)
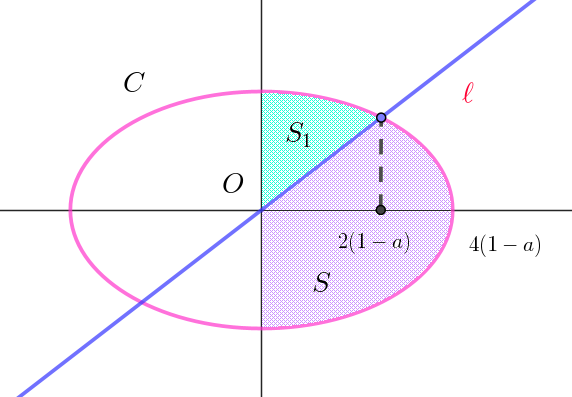
$\sqrt{3}ax \geqq (1-a)y \quad より \quad y \leqq \cfrac{\sqrt{3}a}{1-a} x$
$y =\cfrac{\sqrt{3}a}{1-a} x \ \ を \ \ \ell \ \ とおく。$
$楕円 \ C\ で囲まれた部分と連立不等式の表す領域の共通部分は$
$右図の紫色で表された部分であるが、先に水色で表された部分$
$の面積 \ S_1\ を求める。$
$C \ と \ \ell \ の交点は$
\[
\hspace{1em}
\left\{ \begin{array}{l}
\cfrac{x^2}{16(1-a)^2}+ \cfrac{y^2}{16a^2}=1 \hspace{5em}①\\
y =\cfrac{\sqrt{3}a}{1-a} x \hspace{10em}②\\
\end{array} \right.
\]
$②を①に代入して$
$\cfrac{x^2}{(1-a)^2}+ \cfrac{3a^2x^2}{a^2(1-a)^2}=16$
$\cfrac{4x^2}{(1-a)^2} =16$
$x^2=4(1-a)^2$
$x \geqq 0 \ \ より \ \ x=2(1-a)$
$①式は \quad y=\cfrac{a}{1-a}\sqrt{16(1-a)^2-x^2} \quad だから$
\begin{eqnarray*}
S_1
&=&\int _0^{2(1-a)} \big(\cfrac{a}{1-a}\sqrt{16(1-a)^2-x^2} - \cfrac{\sqrt{3}a}{1-a} x \big)dx\\
\\
&=&\cfrac{a}{1-a}\int _0^{2(1-a)} \big(\sqrt{16(1-a)^2-x^2} - \sqrt{3} x \big) dx\\
\\
\end{eqnarray*}
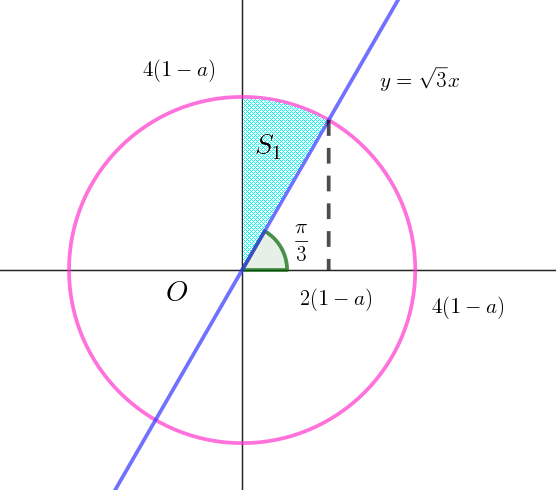
$この定積分からわかるように、S_1\ \ の積分部分は右図のとおり、$
$半径 \ 4(1-a),\quad 中心角 \ \cfrac{\pi}{6}\ \ の扇形の面積に一致する。$
$S_1=\cfrac{a}{1-a} \times \pi \big(4(1-a)\big)^2 \times \cfrac{1}{12}=\cfrac{4}{3}\pi a (1-a)$
$求める面積Sは$
\begin{eqnarray*}
S
&=&\cfrac{1}{2} \times (楕円の面積) -S_1\\
\\
&=&\cfrac{1}{2} \times \pi \times 4(1-a) \times 4a -\cfrac{4}{3}\pi a (1-a)\\
\\
&=&8\pi a(1-a)-\cfrac{4}{3}\pi a (1-a)\\
\\
&=&\cfrac{20}{3}\pi a (1-a)\\
\end{eqnarray*}
(3)
\begin{eqnarray*}
S
&=&\cfrac{20}{3}\pi a (1-a)\\
\\
&=&-\cfrac{20}{3}\pi (a^2-a)\\
\\
&=&-\cfrac{20}{3}\pi \big\{(a-\dfrac{1}{2})^2-\dfrac{1}{4}\big\}\\
\\
&=&-\cfrac{20}{3}\pi (a-\dfrac{1}{2})^2 + \dfrac{5}{3}\pi \\
\end{eqnarray*}
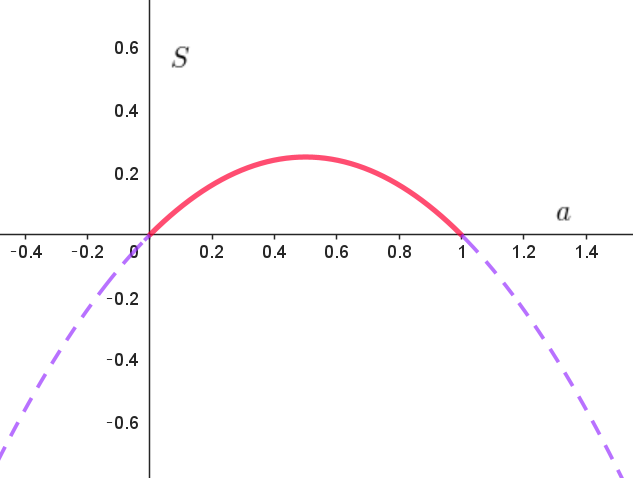
$0< a < 1 \quad だから \quad a=\cfrac{1}{2} \ \ のとき \ S\ は最大値 \ \ \cfrac{5}{3}\pi \ \ をもつ。$
メインメニュー に戻る