MY MATH NOTE

新潟大学(理系) 2024年　問題3

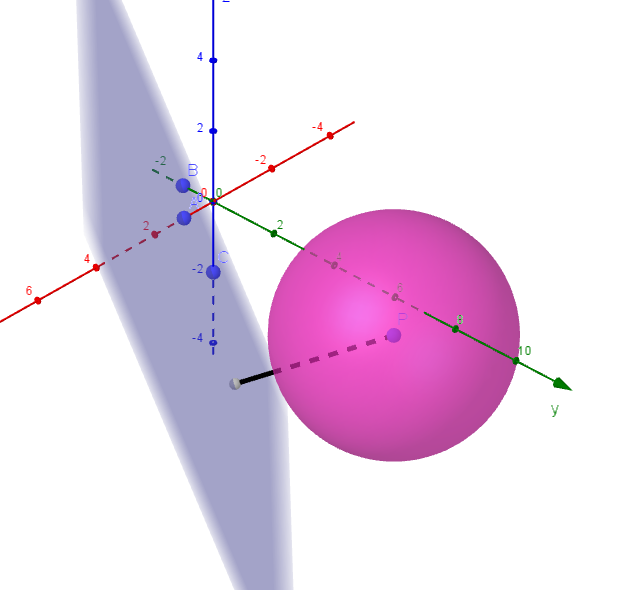
$座標空間において、3\ 点A(1,\ 0,\ 0),\ \ B(0,\ -1,\ 0),\ \ C(0,\ 0,\ -2)\ \ の定める平面を \ \alpha \ とし、方程式$
$x^2+y^2+z^2+2x-10y+4z+21=0 \ \ が表す球面を \ S\ とする。次の問いに答えよ。$
$(1)\ \ 球面 \ S\ の中心 \ P\ の座標と \ S\ の半径を求めよ。$
$(2)\ \ 実数 \ s,\ t\ に対して、点D\ を \ \vec{AD}=s\vec{AB}+t \vec{AC}\ \ を満たすようにとる。このとき、D\ の座標を$
$\quad s,\ t\ を用いて表せ。$
$(3)\ \ 点\ Qが平面 \ \alpha \ 上を動き、点R\ が球面 \ S\ 上を動くとき、Q\ と \ R\ の距離の最小値を求めよ。$
$\quad また、そのときの \ Q\ と \ R\ の座標をそれぞれ求めよ。$

(1)

　
$x^2+y^2+z^2+2x-10y+4z+21=0 $

$(x+1)^2+(y-5)^2+(z+2)^2=9 \quad だから$

$中心 \ \ P(-1,\ 5,\ -2) , \qquad 半径 \ \ r=3$

(2)

(3)

　
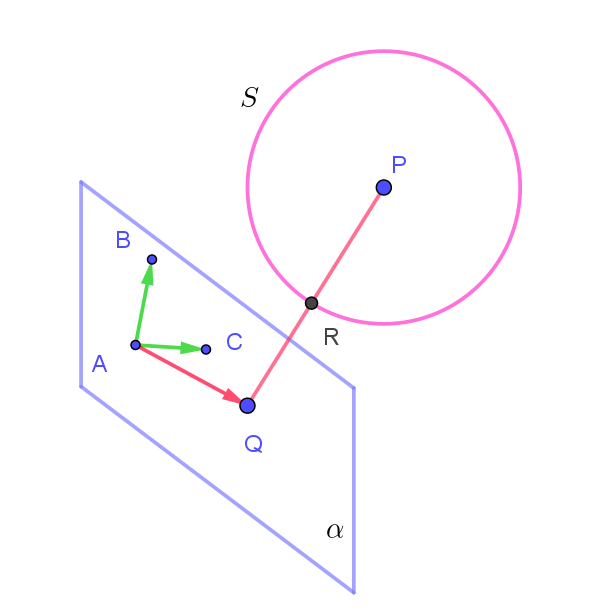
$点P\ と点Q\ の距離が最小になるのは、PQ \perp \alpha \quad のときだから$

$PQ \perp AB,\quad PQ \perp AC$

$\vec{AB}=\vec{OB}-\vec{OA}=(0,\ -1,\ 0)-(1,\ 0,\ 0)=(-1,\ -1,\ 0)$

$\vec{AC}=\vec{OC}-\vec{OA}=(0,\ 0,\ -2)-(1,\ 0,\ 0)=(-1,\ 0,\ -2)$

$点Q\ は平面 \ \alpha \ \ 上にあるから、\vec{AQ}=s\vec{AB}+t \vec{AC}\ \ とおける。(2)より$

$Q(1-s-t,\ -s,\ -2t)$

$\vec{PQ}=\vec{OQ}-\vec{OP}=(1-s-t,\ -s,\ -2t) - (-1,\ 5,\ -2)=(2-s-t,\ -5-s,\ 2-2t)$

$PQ \perp AB \quad より \quad \vec{PQ}\cdot \vec{AB}=0 \qquad -(2-s-t)-(-5-s)=0$

$ \quad 2s+t=-3 \hspace{5em}①$

$PQ \perp AC \quad より \quad \vec{PQ}\cdot \vec{AC}=0 \qquad -(2-s-t)-2(2-2t)=0$

$ \quad s+5t=6 \hspace{5em}②$

$①②を解いて \quad s=-\cfrac{7}{3}, \quad t=\cfrac{5}{3},\qquad 1-s-t=1 +\cfrac{7}{3}-\cfrac{5}{3}=\cfrac{5}{3}$

$ゆえに \quad Q(\cfrac{5}{3},\ \cfrac{7}{3},\ -\cfrac{10}{3})$


$(別解)$

　
$平面 \ \alpha \ を \ \ ax+by+cz=d \quad とおくと$

$点A(1,\ 0,\ 0) \quad を通るから \quad a=d$

$点B(0,\ -1,\ 0) \quad を通るから \quad -b=d \qquad b=-d$

$点C(0,\ 0,\ -2) \quad を通るから \quad -2c=d \qquad c=-\cfrac{d}{2}$

$\alpha \ は \quad dx-dy-\cfrac{d}{2}z=d \quad より \quad 2x-2y-z=2$

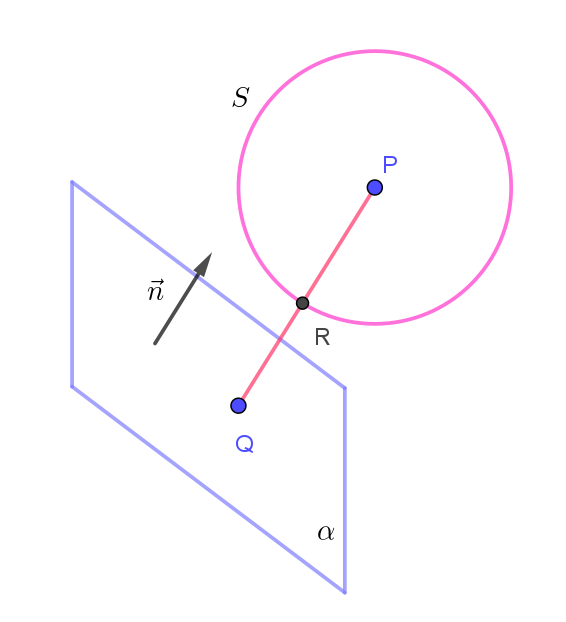
$\alpha \ の法線ベクトルを右図のようにとると \quad \vec{n}=(-2,\ 2,\ 1)$

$Q\ と \ R\ の距離が最小となるのは、3\ 点 \ P,\ R,\ Q\ が一直線上にあるときである。$

$\vec{QP}=k\vec{n}$

$\vec{OP}-\vec{OQ}=k\vec{n}$

$\vec{OQ}=\vec{OP}-k\vec{n}=(-1,\ 5,\ -2)-k(-2,\ 2,\ 1)=(-1+2k,\ 5-2k,\ -2-k)$

$点Q(-1+2k,\ 5-2k,\ -2-k)\ \ は平面 \ \alpha \ \ 上にあるから$

$2(-1+2k)-2(5-2k)-(-2-k)=2$

$9k=12 \qquad k=\cfrac{4}{3}$

$ゆえに \quad Q(\cfrac{5}{3},\ \cfrac{7}{3},\ -\cfrac{10}{3})$

$\vec{QP}=k\vec{n}=\cfrac{4}{3}(-2,\ 2,\ 1)=\big(-\dfrac{8}{3},\ \dfrac{8}{3},\ \dfrac{4}{3}\big) \hspace{5em}( または \quad \vec{QP}=\vec{OP}-\vec{OQ} \quad で求めてもよい)$

$QP^2=\big(-\dfrac{8}{3})^2+\big(\dfrac{8}{3}\big)^2+ \big(\dfrac{4}{3}\big)^2=16$

$よって Q\ と \ R\ の距離の最小値は \quad QR=QP-PR=4-3=1$

$点R\ は線分 \ QP\ を \ \ 1:3\ \ に内分する点だから$

$R\big(\dfrac{3 \times \dfrac{5}{3}+1 \times (-1)}{4},\ \dfrac{3 \times \dfrac{7}{3}+1 \times 5}{4},\ \dfrac{3 \times (-\dfrac{10}{3}) +1 \times (-2)}{4}\big)$

$R(1,\ 3,\ -3)$

ページの先頭へ↑