MY MATH NOTE

新潟大学(理系) 2024年　問題2

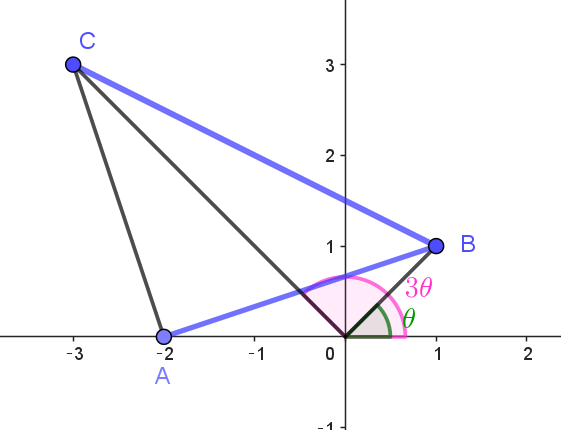
$座標平面上の原点を\ O\ とし、3\ 点A(-2,\ 0),\ \ B(\cos \theta,\ \sin \theta),\ \ C(3\cos 3\theta,\ 3\sin 3\theta)\ \ をとる。$
$ただし、0 \leqq \theta \leqq \cfrac{2\pi}{3} \ \ とする。次の問いに答えよ。$
$(1)\ \ AB^2 \ \ と \ \ BC^2 \ \ を \ \cos \theta \ を用いて表せ。$
$(2)\ \ 0 \leqq \theta \leqq \cfrac{2\pi}{3} \ \ のとき、AB^2+BC^2 \ \ の最大値と最小値を求めよ。また、そのときの点B\ と点C\ の$
$\quad 座標をそれぞれ求めよ。$

(1)

　
\begin{eqnarray*} AB^2 &=&(\cos \theta +2)^2+\sin ^2\theta\\ \\ &=&(\cos ^2 \theta +4\cos \theta + 4) +\sin ^2\theta\\ \\ &=&5+4\cos \theta \end{eqnarray*}
\begin{eqnarray*} BC^2 &=&(3\cos 3\theta - \cos \theta )^2+ (3\sin 3\theta - \sin \theta)^2\\ \\ &=&9(\cos ^2 3\theta + \sin ^2 3\theta) +(\cos ^2 \theta + \sin ^2 \theta) -6(\cos 3\theta \cos \theta + \sin 3\theta \sin \theta)\\ \\ &=&10- 6\cos (3\theta - \theta)\\ \\ &=&10- 6\cos 2\theta \\ \\ &=&10- 6(2\cos ^2\theta -1)\\ \\ &=&16 -12\cos ^2\theta \end{eqnarray*}

(2)

　
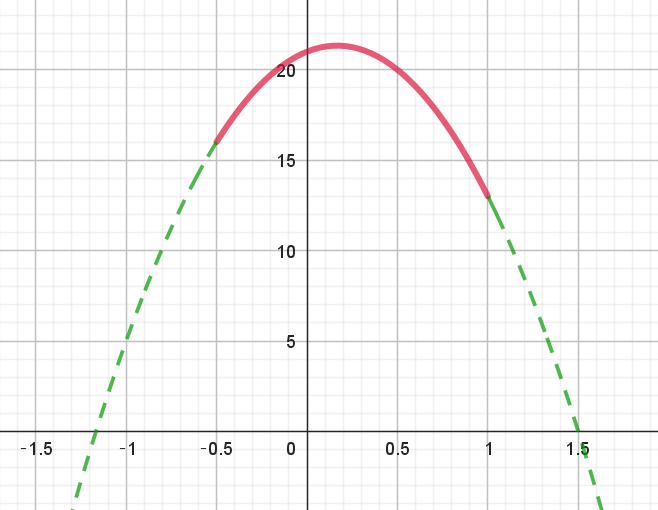
$y=f(t) \ \ のグラフは右図のとおりで$

$最大値は$

$t=\cfrac{1}{6} \quad すなわち \quad \cos \theta=\cfrac{1}{6} \quad のとき \ \ \cfrac{64}{3}\ \ をとる。$

$このとき$

$\sin \theta=\sqrt{1-(\dfrac{1}{6})^2}=\cfrac{\sqrt{35}}{6}$

$\cos 3\theta=4\cos ^3 \theta -3\cos \theta=4 \times \big(\dfrac{1}{6}\big)^3-3 \times \dfrac{1}{6}=-\cfrac{13}{27}$

$\sin 3\theta=3\sin \theta -4\sin ^3\theta=3 \times \cfrac{\sqrt{35}}{6} - 4 \times \big(\dfrac{\sqrt{35}}{6}\big)^3=-\cfrac{4\sqrt{35}}{27}$

$よって \quad B(\cfrac{1}{6},\ \cfrac{\sqrt{35}}{6}),\quad C(-\cfrac{13}{9},\ -\cfrac{4\sqrt{35}}{9})$

$最小値は$

$t=1 \quad すなわち \quad \cos \theta=1 \quad のとき \ \ 13\ \ をとる。$

$このとき \quad \theta=0 \quad だから$

$\sin \theta=0 ,\qquad \cos 3\theta=1, \qquad \sin 3\theta=0$

$よって \quad B(1,\ 0),\quad C(3,\ 0)$

ページの先頭へ↑