新潟大学(理系) 2024年　問題1


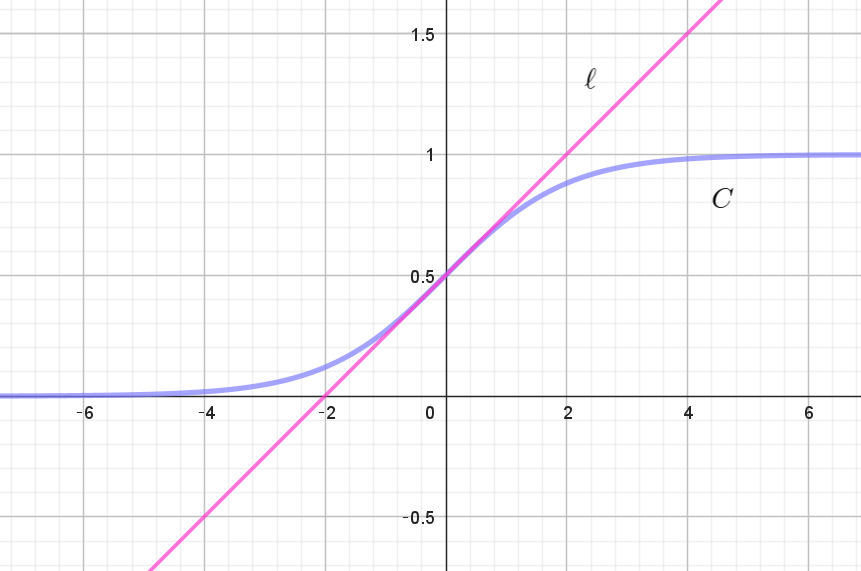
$f(x)=\dfrac{e^x}{e^x+1} \ \ とする。曲線 \ C:y=f(x)\ の点 \big(0,\ \dfrac{1}{2}\big)\ における接線を \ \ell \ とする。次の問いに答えよ。$
\[(1)\ \ \int f(x)dx \ \ を求めよ。\] $(2)\ \ 接線 \ \ell \ の方程式を求めよ。$
$(3)\ \ 曲線 \ C\ と接線 \ \ell \ は点 \big(0,\ \dfrac{1}{2}\big)\ \ 以外に共有点を持たないことを示せ。$
$(4)\ \ 曲線 \ C ,\ 接線 \ \ell \ ,\ y\ 軸および直線 \ x=1 \ で囲まれる図形の面積を求めよ。$


(1)


\[\int f(x)dx =\int \dfrac{e^x}{e^x+1}dx \quad において\]
$e^x+1=t \quad とおくと \quad e^xdx=dt \quad だから$

\[\int \dfrac{e^x}{e^x+1}dx =\int \dfrac{dt}{t} =\log t +C =\log (e^x +1) +C \]

(2)

　

$f'(x)=\cfrac{e^x(e^x+1)-e^x e^x}{(e^x+1)^2}=\cfrac{e^x}{(e^x+1)^2}$

$f'(0)=\cfrac{1}{(1+1)^2}=\cfrac{1}{4}$

$\big(0,\ \dfrac{1}{2}\big)\ における接線 \ \ell \ の方程式は$

$y=\cfrac{1}{4}x + \cfrac{1}{2}$


(3)


$曲線 \ C\ と接線 \ \ell \ の共有点は$

$\dfrac{e^x}{e^x+1}=\cfrac{1}{4}x + \cfrac{1}{2} \quad の解である。$

$4e^x=x(e^x+1)+2(e^x+1)$

$(x-2)e^x+x+2=0$

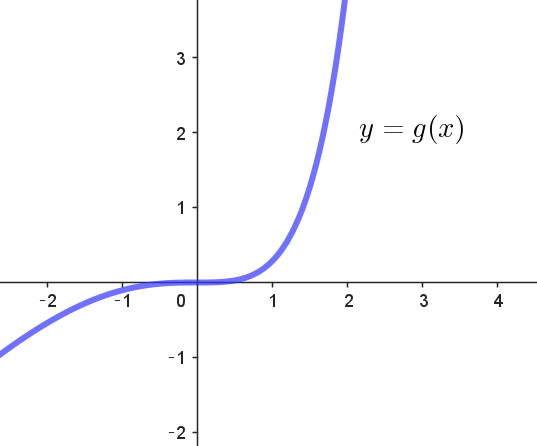
$g(x)=(x-2)e^x+x+2 \quad とおくと$

$g'(x)=e^x+(x-2)e^x+1=(x-1)e^x+1$

$g''(x)=e^x+(x-1)e^x=xe^x$

　

(i)$\ \ x > 0 \ \ のとき \ \ g''(x) > 0 \ \ だから \ g'(x)\ は単調増加 となり$

$ \ \ g'(x) > g'(0)=0$

(ii)$\ \ x < 0 \ \ のとき \ \ g''(x) < 0 \ \ だから \ g'(x)\ は単調減少 となり$

$ \ \ g'(x) > g'(0)=0$

(i),(ii)$\ \ より g'(x)>0 \ \ だから \ \ g(x)\ は単調増加$

$g(0)=-2e^0+2=0 $

$したがって \quad g(x)=0 \ \ の解は \ \ x=0 \ \ のみ$

$よって \ \ 曲線 \ C\ と接線 \ \ell \ は点 \big(0,\ \dfrac{1}{2}\big)\ \ 以外に共有点を持たない。$


(4)

　

$f'(x)=\cfrac{e^x}{(e^x+1)^2} \quad より$

$f''(x)=\cfrac{e^x(e^x+1)^2-2e^x(e^x+1)e^x}{(e^x+1)^4}=\cfrac{e^x(e^x+1)-2e^{2x}}{(e^x+1)^3}=\cfrac{e^x(1-2e^x)}{(e^x+1)^3}$

$x > 0 \ \ のとき \ \ e^x > 1 \ \ だから \ \ 1-2e^x < 0 \ \ よって \ \ f''(x) < 0$

$y=f(x)\ のグラフは \ x > 0\ \ で上に凸となり、y=f(x)\ の接線は$

$y=f(x)\ のグラフの上にある。$

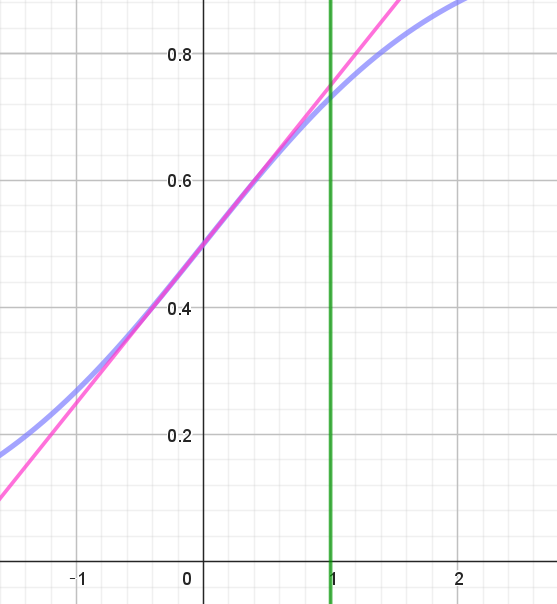
$求める面積 \ S\ は$

\begin{eqnarray*} S &=&\int_0^1 \big(\dfrac{1}{4}x+\dfrac{1}{2}-\dfrac{e^x}{e^x+1}\big)dx\\ \\ &=&\big[\dfrac{x^2}{8}+\dfrac{x}{2}-\log(e^x+1)\big]_0^1\\ \\ &=&\cfrac{1}{8}+\cfrac{1}{2}-\log(e+1)+\log 2\\ \\ &=&\cfrac{5}{8} -\log(e+1)+\log 2\\ \end{eqnarray*}
$なお、このSの値は右のグラフからわかるとおり、0.00489\ \ と非常に小さな値です。$


$(補充)$

$f(x)=\cfrac{e^x}{e^x+1} \ \ のグラフは点 \big(0,\ \dfrac{1}{2}\big)\ に関して点対称である。$

$(証明)$

$曲線\ C\ 上の任意の点P(x,\ y)\ の点 \big(0,\ \dfrac{1}{2}\big)\ に関する対称点をP'(x',\ y')\ とおくと$

$\cfrac{x+x'}{2}=0 ,\qquad \cfrac{y+y'}{2}=\cfrac{1}{2}$

$x=-x',\qquad y=1-y'$

$点P(x,\ y)\ は曲線 \ C\ 上の点だから \quad y=\cfrac{e^x}{e^x+1}$

$1-y'=\cfrac{e^{-x'}}{e^{-x'}+1}$

$y'=1-\cfrac{e^{-x'}}{e^{-x'}+1}=\cfrac{(e^{-x'}+1)-e^{-x'}}{e^{-x'}+1}=\cfrac{1}{e^{-x'}+1}=\cfrac{e^{x'}}{e^{x'}+1}$

$したがって \quad P'(x',\ y')\ も曲線 \ C\ 上の点である。$


ページの先頭へ↑




メインメニュー　に戻る