名古屋大学 2025年 問題4
$コイン \ ①,\ \cdots ,\ ⑥\ が下図のようにマス目の中に置かれている。$
$\hspace{5em}$
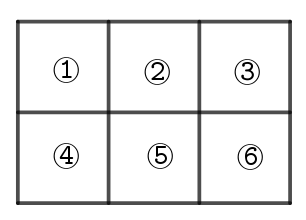
$これらのコインから無作為にひとつを選び、選んだコインはそのままにし、そのコインのあるマス目と辺を$
$共有して隣接するマス目のコインを裏返す操作を考える。例えば、①を選べば、②,④を裏返し、②を選べ$
$ば、①、②、③を裏返す。最初はすべてのコインが表向きに置かれていたとする。正の整数 \ n\ に対し、n\ 回$
$目の操作終了時点ですべてのコインが裏向きである確率を \ p_n \ とするとき、以下の問に答えよ。$
$(1)\ \ p_2 \ を求めよ。$
$(2)\ \ コイン \ ①,\ \cdots ,\ ⑥をグループ \ A,\ B\ に分けることによって、n\ 回目の操作終了時点ですべてのコインが$
$\quad 裏向きであるための必要十分条件を次の形に表すことができる。$
$\qquad n\ 回目の操作終了時点までに \ A\ に属する各コインはそれぞれ奇数回選ばれ、B\ に属する各コインはそれ$
$\qquad ぞれ偶数回選ばれる。$
$\quad どのようにグループ分けすればよいかを答えよ。$
$(3)\ \ p_4 を求めよ。$
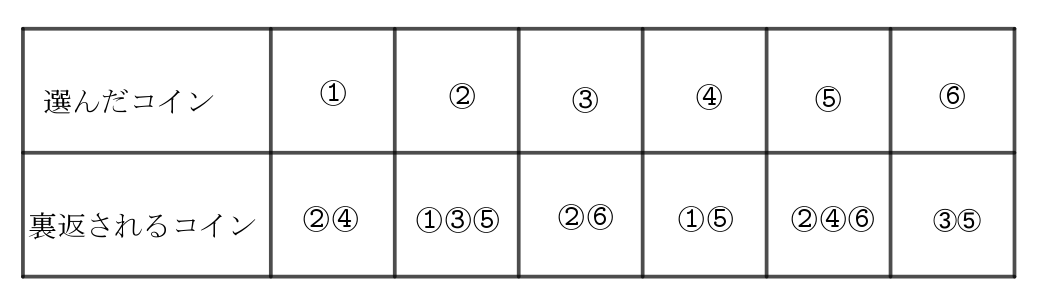
$裏返されるコインをまとめたものである。$
(1)
$2\ 回目の操作終了時点ですべてのコインが裏向きになるのは、②、⑤の順にコインを選んだ場合と$
$⑤、②の順にコインを選んだ場合の \ 2\ 通りがあるから$
$P_2=\dfrac{1}{6} \times \dfrac{1}{6} \times 2=\dfrac{1}{18}$
(2)
$②と⑤をグループA 、①、③、④、⑥をグループB に分ければよい。$
$n\ が偶数のとき、n\ 回の操作のうち、②、⑤のコインをそれぞれ奇数の \ (2k-1)\ 回選べば①~⑥のすべてのコインを$
$裏返すことができる。残り \ n-2(2k-1)\ 回は、①、③、④、⑥のコインをそれぞれ偶数回選べば、すべてのコイン$
$は表は表、裏は裏のままになる。$
$したがって、n\ が奇数のときはすべてのコインを裏返すことはできない。$
(3)
$4\ 回の操作のうち、②、⑤のコインはそれぞれ奇数回選ばれるから$
(i)$\ \ ②、⑤のコインが \ 1\ 回ずつ選ばれる場合$
$\quad その場合の数は \quad {}_4P_2 \ \ 通り$
$\quad 残り \ 2\ 回は、①、③、④、⑥のコインをそれぞれ \ 2\ 回選べばよい。その場合の数は \ \ 4\ \ 通り$
$\quad よって \quad {}_4P_2 \times 4 =48 \ \ 通り$
(ii)$\ \ ②のコインが \ 3\ 回,⑤のコインが \ 1\ 回選ばれる場合$
$\quad {}_4C_3=4 \ \ 通り$
(iii)$\ \ ②のコインが \ 1\ 回,⑤のコインが \ 3\ 回選ばれる場合$
$\quad {}_4C_1=4 \ \ 通り$
(i),(ii),(ii),$\ \ は互いに排反だから合わせて \quad 48+4+4=56 \ \ 通り$
$p_4=\cfrac{56}{6^4}=\cfrac{7}{162}$
メインメニュー に戻る