名古屋大学(理系) 2025年　問題3


$以下の問に答えよ。$
$(1)\ \ 実数 \ r,\ \alpha \ は \ \ 0 < r \leqq 1, \ \ 0 \leqq \alpha < \pi \ \ をみたすとする。xy\ 平面内で、点(1,\ 0)\ を中心にもつ半径 \ r\ の円周$
$\quad およびその内部を \ C\ とする。C\ を原点(0,\ 0)\ を中心に反時計まわりに角度 \ \alpha \ だけ回転させるとき、C\ が$
$\quad 通過する領域の面積を求めよ。$
$(2)\ \ 実数 \ R,\ \alpha \ は \ \ 0 < R \leqq 1, \ \ 0 \leqq \alpha < \pi \ \ をみたすとする。xyz\ 空間内で、点(1,\ 0,\ 0)\ を中心にもつ半径 \ R\ の$
$\quad 球面およびその内部を \ B\ とする。B\ を \ x\ 軸のまわりに角度 \ \alpha \ だけ回転させるとき、B\ が通過する領域の$
$\quad 体積を求めよ。ただし、回転の向きは回転後の \ B\ の中心が \ \ (\cos \alpha,\ \sin \alpha,\ 0)\ になるように選ぶものとする。$


(1)

　

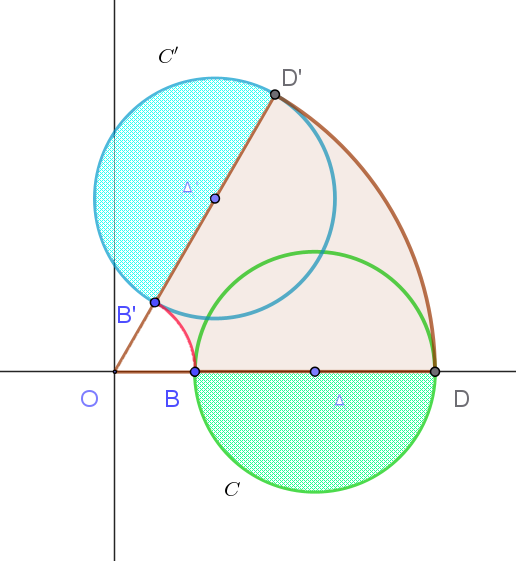
$円 \ C\ の \ x\ 軸上の中心 \ A,\ 直径の両端 \ BD\ を、原点を中心に \ \alpha \ 回転させた$

$とき、それぞれ \ A',\ B'D'\ に移るとすると \ C\ が通過する領域は右図の$

$ように扇型 \ ODD' \ から扇型 \ OBB'\ を除いた薄茶色の部分と、BD\ を直径$

$とする緑色の半円とB'D'\ を直径とする青色の半円であるから$

$求める面積 \ S\ は$
\begin{eqnarray*} S &=&\pi\{(1+r)^2-(1-r)^2\} \times \dfrac{\alpha}{2\pi} +\pi r^2\\ \\ &=&4\pi r \times \dfrac{\alpha}{2\pi} +\pi r^2\\ \\ &=&2r\alpha + \pi r^2\\ \end{eqnarray*}

　

(2)


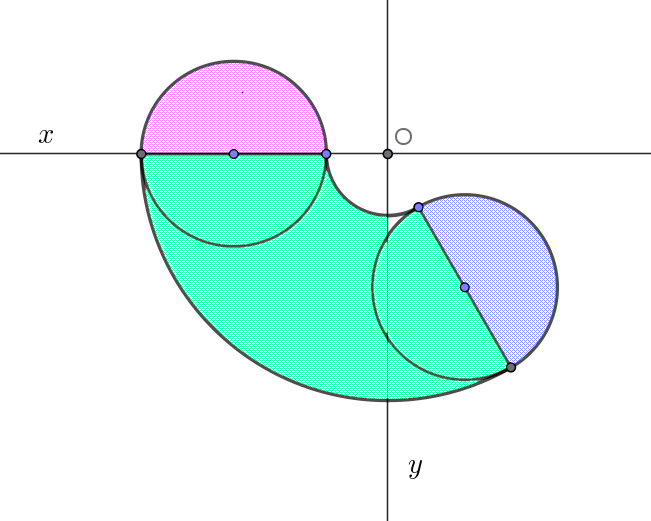
$右図は \ B\ が通過する領域を \ xy\ 平面に射影した図である。$

$ピンク色と青色の半球と緑色の円環体(トーラス)から成っている。$

$円環体は球面 \ \ (x-1)^2+y^2+z^2=R^2 \ \ で \ y=0\ とおいた \ xz\ 平面で$

$考えると、円\ x=1 \pm \sqrt{R^2-z^2} \ を \ z\ 軸のまわりに角度 \ \alpha \ だけ回転$

$させた立体である。$

　

$求める体積 \ V\ は$

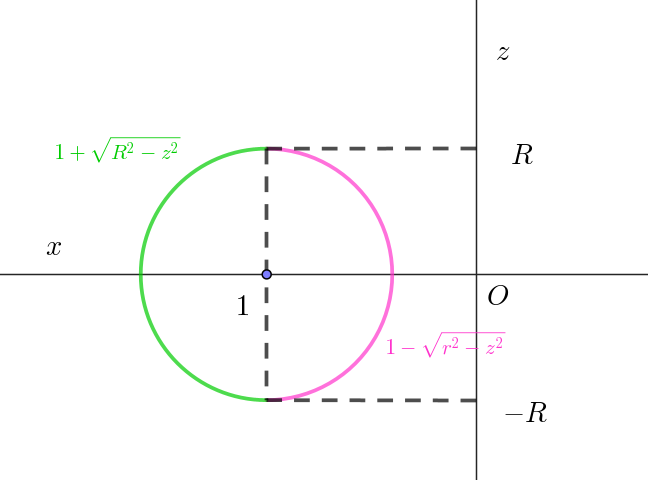
\begin{eqnarray*} V &=&\big\{\pi \int_{-R}^R(1+\sqrt{R^2-z^2})^2dz - \pi \int_{-R}^R(1-\sqrt{R^2-z^2})^2dz\big\} \times \dfrac{\alpha}{2\pi} \\ \\ & &\qquad + \dfrac{4}{3}\pi R^3\\ \\ &=&\alpha \int_0^R \{(1+\sqrt{R^2-z^2})^2 -(1-\sqrt{R^2-z^2})^2 \} dz + \dfrac{4}{3}\pi R^3\\ \\ &=&4\alpha \int_0^R \sqrt{R^2-z^2} dz + \dfrac{4}{3}\pi R^3\\ \\ &=&4\alpha \times \dfrac{1}{4} \times \pi R^2 + \dfrac{4}{3}\pi R^3\\ \\ &=&\pi R^2 \alpha + \dfrac{4}{3}\pi R^3\\ \end{eqnarray*}

ページの先頭へ↑



メインメニュー　に戻る