MY MATH NOTE

名古屋大学（理系）2019年前期　問題1　別解

$(3) \quad xyz空間においてxy平面内の原点を中心とする半径1の円板をDとする。Dを底面とし、点(0,0,1)を$
$\quad 頂点とする円錐をCとする。Cを平面x=\dfrac{1}{2}で2つの部分に切断したとき、小さい方をSとする。$
$\quad$ x軸に垂直な平面による切り口$を考えてSの体積を求めてみましょう。$

　
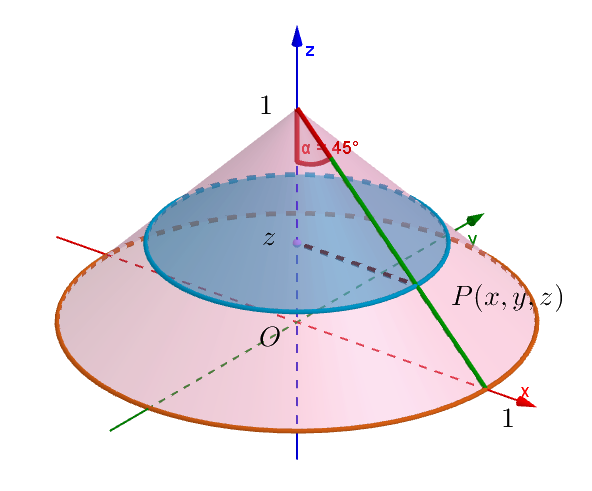
$この直円錐をz軸に垂直な平面で切った切り口はz軸上に中心をもつ円だから、$
$その半径をrとすると$

$\qquad r^2=x^2+y^2$

$z軸と母線のなす角は45°だから　r=1-z$
$よって$
$\qquad (1-z)^2=x^2+y^2$

$\qquad 1-z=\sqrt{x^2+y^2}$

$\qquad \therefore z=1-\sqrt{x^2+y^2}$

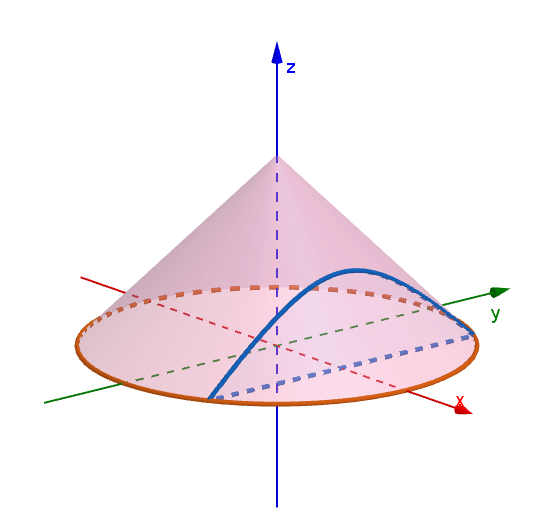
$これが、円錐面の方程式です。$

$この直円錐をx軸に垂直な平面で切った切り口の面積Tは$
\begin{eqnarray*} T &=&2\int _0^{\sqrt{1-x^2}}\bigl(1-\sqrt{x^2+y^2}\bigr)dy\\ \\ &=&2\int _0^{\sqrt{1-x^2}}dy-\underbrace{2\int _0^{\sqrt{1-x^2}}\sqrt{x^2+y^2}dy}_{\substack{\large この積分は後述別記を参照}}\\ \\ &=&2\bigl[\ y\ \bigr]_0^{\sqrt{1-x^2}}-\bigl[y\sqrt{x^2+y^2}+x^2\log(y+\sqrt{x^2+y^2})\bigr]_0^{\sqrt{1-x^2}}\\ \\ &=&2\sqrt{1-x^2}-\sqrt{1-x^2}\sqrt{x^2+(1-x^2)}-x^2\log (\sqrt{1-x^2}+\sqrt{x^2+(1-x^2)}\ )+x^2\log \sqrt{x^2}\\ \\ &=&\sqrt{1-x^2}-x^2\log (1+\sqrt{1-x^2})+x^2\log x\\ \end{eqnarray*} $したがって$
\[V=\int _{\small{\dfrac{1}{2}}}^1 Tdx =\int _{\small{\dfrac{1}{2}}}^1 \bigl\{\sqrt{1-x^2}-x^2\log (1+\sqrt{1-x^2})+x^2\log x\bigr\}dx\] $積分項を順にp_1,p_2.p_3とおくと$

$\qquad V= p_1-p_2+p_3$

$(1)\ \ p_1 の計算$

　
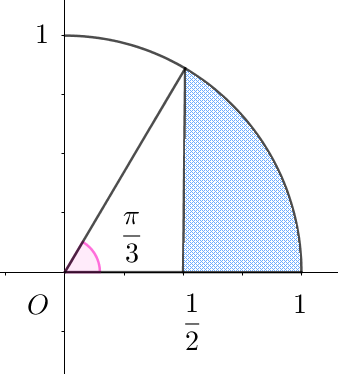
$p_1 は右図の青色の領域の面積だから$
\begin{eqnarray*} p_1 &=&\int _{\small{\dfrac{1}{2}}}^1 \sqrt{1-x^2}dx\\ &=&\pi \times \cfrac{1}{6}-\cfrac{1}{2}\times \cfrac{1}{2}\times 1 \times \sin \cfrac{\pi}{3}\\ &=&\cfrac{\pi}{6}-\cfrac{\sqrt{3}}{8}\\ \end{eqnarray*}
$(2)\ \ p_2の計算$

\[p_2=\int _{\small{\dfrac{1}{2}}}^1 x^2\log (1+\sqrt{1-x^2})dx \ \ は部分積分法で求める\] $\qquad \log (1+\sqrt{1-x^2})が積分項であるが、その積分も部分積分法で求める。$
\begin{eqnarray*} \int \log (1+\sqrt{1-x^2})dx &=&x\log (1+\sqrt{1-x^2})-\int x \times \cfrac{\cfrac{-x}{\sqrt{1-x^2}}}{1+\sqrt{1-x^2}}dx\\ \\ &=&x\log (1+\sqrt{1-x^2})+\int \cfrac{x^2}{\sqrt{1-x^2}(1+\sqrt{1-x^2}) }dx\\ \\ &=&x\log (1+\sqrt{1-x^2})+\int \cfrac{x^2(1-\sqrt{1-x^2})}{\sqrt{1-x^2}(1-(1-x^2))}dx\\ \\ &=&x\log (1+\sqrt{1-x^2})+\int \cfrac{1-\sqrt{1-x^2}}{\sqrt{1-x^2}}dx\\ \\ &=&x\log (1+\sqrt{1-x^2})+\int \cfrac{dx}{\sqrt{1-x^2}}-\int dx\\ \\ &=&x\log (1+\sqrt{1-x^2})+\sin ^{-1}x-x\\ \end{eqnarray*} $よって$
\[p_2=\bigl[x^2(x\log (1+\sqrt{1-x^2})+\sin ^{-1}x-x\bigr]_{\small{\dfrac{1}{2}}}^1 -\int _{\small{\dfrac{1}{2}}}^1 2x\bigl\{x\log (1+\sqrt{1-x^2})+\sin ^{-1}x-x\bigr\}dx\] (i)$定数項をAとおくと$
\begin{eqnarray*} A &=&\sin ^{-1}1-1-\cfrac{1}{4}\bigl\{\cfrac{1}{2}\log(1+\cfrac{\sqrt{3}}{2})+\sin ^{-1}\cfrac{1}{2}-\cfrac{1}{2}\bigr\}\\ &=&\cfrac{\pi}{2}-1-\cfrac{1}{8}\log(1+\cfrac{\sqrt{3}}{2})-\cfrac{1}{4}\times \cfrac{\pi}{6}+\cfrac{1}{8}\\ &=&\cfrac{\pi}{2}-1-\cfrac{1}{8}\log(\cfrac{2+\sqrt{3}}{2})-\cfrac{\pi}{24}+\cfrac{1}{8}\\ &=&-\cfrac{7}{8}+\cfrac{11}{24}\pi-\cfrac{1}{8}\log(2+\sqrt{3})+\cfrac{1}{8}\log 2\\ \end{eqnarray*} (ii)$積分項は$
\[2\int _{\small{\dfrac{1}{2}}}^1 x^2\log (1+\sqrt{1-x^2})dx+ 2\int _{\small{\dfrac{1}{2}}}^1 x\sin ^{-1}xdx -2\int _{\small{\dfrac{1}{2}}}^1 x^2dx\] $\quad 第1項は2p_2である。第2項をq_2とおくと$
\begin{eqnarray*} q_2 &=&\int _{\small{\dfrac{1}{2}}}^1 2x\sin ^{-1}xdx\\ &=&\bigl[x^2\sin ^{-1}x\bigr]_{\small{\dfrac{1}{2}}}^1 -\int _{\small{\dfrac{1}{2}}}^1 x^2\cdot \cfrac{dx}{\sqrt{1-x^2}}\\ &=&\sin ^{-1}1-\cfrac{1}{4}\sin ^{-1}\cfrac{1}{2} -\int _{\small{\dfrac{1}{2}}}^1 \cfrac{x^2}{\sqrt{1-x^2}}dx\\ &=&\cfrac{\pi}{2}-\cfrac{1}{4}\times \cfrac{\pi}{6} +\int _{\small{\dfrac{1}{2}}}^1 \cfrac{-x^2}{\sqrt{1-x^2}}dx\\ &=&\cfrac{11}{24}\pi +\int _{\small{\dfrac{1}{2}}}^1 \cfrac{1-x^2-1}{\sqrt{1-x^2}}dx\\ &=&\cfrac{11}{24}\pi +\int _{\small{\dfrac{1}{2}}}^1 \sqrt{1-x^2}dx -\int _{\small{\dfrac{1}{2}}}^1 \cfrac{1}{\sqrt{1-x^2}}dx\\ &=&\cfrac{11}{24}\pi +p_1 -\bigl[\sin ^{-1}x \bigr] _{\small{\dfrac{1}{2}}}^1 \\ &=&\cfrac{11}{24}\pi +\bigl(\cfrac{\pi}{6}-\cfrac{\sqrt{3}}{8}\bigr)-\bigl(\sin ^{-1}1-\sin ^{-1}\cfrac{1}{2}\bigr)\\ &=&\cfrac{11}{24}\pi +\bigl(\cfrac{\pi}{6}-\cfrac{\sqrt{3}}{8}\bigr)-\bigl(\cfrac{\pi}{2}-\cfrac{\pi}{6}\bigr)\\ &=&\cfrac{7}{24}\pi -\cfrac{\sqrt{3}}{8}\\ \end{eqnarray*}
$第3項は \ \cfrac{7}{12}\ と簡単に求まる$
$\qquad p_2=A-2p_2-q_2+\cfrac{7}{12}\ \ より$
\begin{eqnarray*} 3p_2 &=&\bigl\{-\cfrac{7}{8}+\cfrac{11}{24}\pi-\cfrac{1}{8}\log(2+\sqrt{3})+\cfrac{1}{8}\log 2\bigr\} -\bigl(\cfrac{7}{24}\pi -\cfrac{\sqrt{3}}{8}\bigr)+\cfrac{7}{12}\\ &=&-\cfrac{7}{24}+\cfrac{\sqrt{3}}{8}+\cfrac{\pi}{6}-\cfrac{1}{8}\log(2+\sqrt{3})+\cfrac{1}{8}\log 2\\ \end{eqnarray*}
$(3)\ \ p_3の計算$

$p_3も部分積分法で求めます。$
\begin{eqnarray*} p_3 &=&\int _{\small{\dfrac{1}{2}}}^1 x^2\log xdx\\ &=&\bigl[\cfrac{x^3}{3}\log x\bigr]_{\small{\dfrac{1}{2}}}^1 -\int _{\small{\dfrac{1}{2}}}^1 \cfrac{x^3}{3} \times \cfrac{1}{x}dx\\ &=&-\cfrac{1}{24}\log \cfrac{1}{2} -\cfrac{1}{3}\int _{\small{\dfrac{1}{2}}}^1 x^2dx\\ &=&\cfrac{1}{24}\log 2 -\cfrac{1}{3}\bigl[\cfrac{x^3}{3}\bigr]_{\small{\dfrac{1}{2}}}^1 \\ &=&\cfrac{1}{24}\log 2 -\cfrac{7}{72}\\ \end{eqnarray*}
$以上より$
\begin{eqnarray*} V &=& p_1-p_2+p_3\\ &=&\bigl(\cfrac{\pi}{6}-\cfrac{\sqrt{3}}{8}\bigr)- \cfrac{1}{3}\bigl(-\cfrac{7}{24}+\cfrac{\sqrt{3}}{8}+\cfrac{\pi}{6}-\cfrac{1}{8}\log(2+\sqrt{3})+\cfrac{1}{8}\log 2\bigr) +\bigl(\cfrac{1}{24}\log 2 -\cfrac{7}{72}\bigr)\\ &=&\cfrac{\pi}{9}-\cfrac{\sqrt{3}}{6} +\cfrac{1}{24}\log (2+\sqrt{3})\\ \end{eqnarray*}

(別記)
\[まず、\int \cfrac{dx}{\sqrt{x^2+A}} \ \ を求めます。\] \[\bigl(\log(x+\sqrt{x^2+A})\bigr)'=\cfrac{1+\cfrac{x}{\sqrt{x^2+A}}}{x+\sqrt{x^2+A}}=\cfrac{\sqrt{x^2+A}+x}{\sqrt{x^2+A}(x+\sqrt{x^2+A})} =\cfrac{1}{\sqrt{x^2+A}} \] $だから$
\[\int \cfrac{dx}{\sqrt{x^2+A}}=\log(x+\sqrt{x^2+A})\]
\begin{eqnarray*} I &=&\int \sqrt{x^2+A}dx\\ &=&x\sqrt{x^2+A}-\int x \cdot \cfrac{x}{\sqrt{x^2+A}}dx\\ &=&x\sqrt{x^2+A}-\int \cfrac{x^2+A-A}{\sqrt{x^2+A}}dx\\ &=&x\sqrt{x^2+A}-\int \bigl(\sqrt{x^2+A}-\cfrac{A}{\sqrt{x^2+A}}\bigr)dx\\ &=&x\sqrt{x^2+A}-I+A\int \cfrac{dx}{\sqrt{x^2+A}}\\ \end{eqnarray*} \begin{eqnarray*} 2I &=&x\sqrt{x^2+A}+A\int \cfrac{dx}{\sqrt{x^2+A}}\\ &=&x\sqrt{x^2+A}+A\log(x+\sqrt{x^2+A})\\ \end{eqnarray*} $\qquad \therefore I=\cfrac{1}{2}\bigl(x\sqrt{x^2+A}+A\log(x+\sqrt{x^2+A})\bigr)$

ページの先頭へ↑