九州大学(理系) 2025年　問題4


$半径 \ 1\ の円周上に反時計回りに点A,\ B,\ C,\ D\ を順にとり、線分AD\ は直径で、AC=CD,\ \ AB=BC\ \ が$
$成り立つとする。$
$(1)\ \ \angle ACB \ \ を求めよ。$
$(2)\ \ BC\ \ を求めよ。 $
$(3)\ \ 線分 \ AC\ と線分 \ BD\ の交点を \ E\ とするとき、三角形 \ BCE\ の面積を求めよ。 $


(1)

　

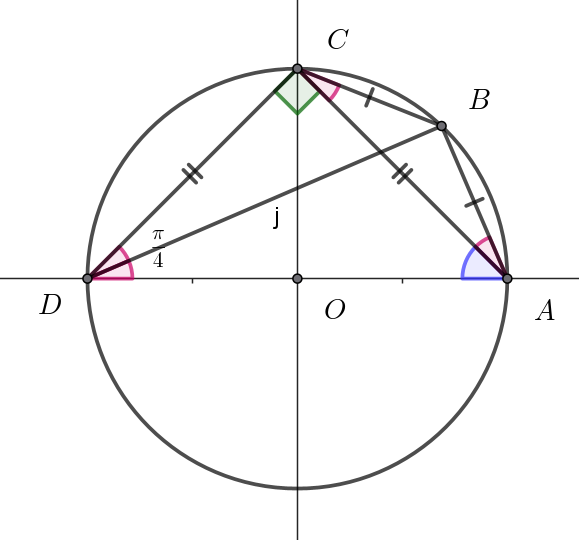
$線分AD\ は直径だから \quad \angle ACD=\dfrac{\pi}{2}$

$\triangle ACD \ において \quad AC=CD \ \ だから \quad \angle ADC=\angle DAC=\dfrac{1}{2} \times (\pi- \dfrac{\pi}{2})=\dfrac{\pi}{4}$

$\triangle ABC \ において \quad AB=BC \ \ だから \quad \angle CAB=\angle ACB,\quad 弧AB=弧BC$

$円周角の定理より \quad \angle CAB=\angle CDB, \quad \angle ACB=\angle ADB$

$よって \quad \angle CDB=\angle ADB$

$\angle CDB + \angle ADB= \angle ADC=\dfrac{\pi}{4} \quad だから \quad \angle ADB=\dfrac{\pi}{8}$

$\angle ACB=\angle ADB=\dfrac{\pi}{8}$


(2)

　

$中心角と円周角の関係より$

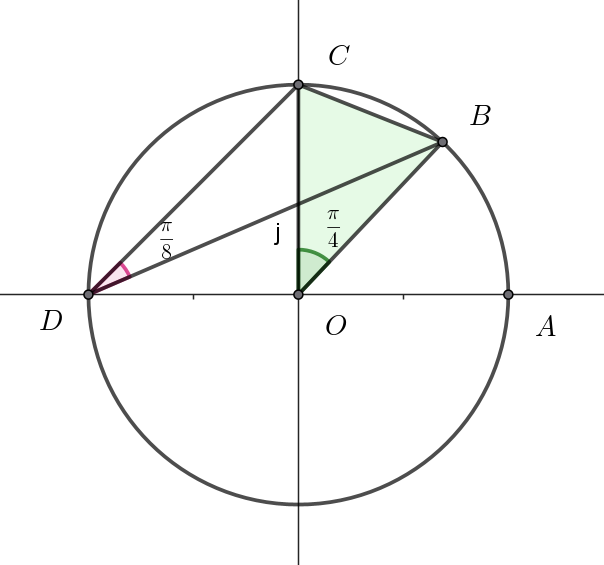
$\angle BOC=2 \times \angle BDC=2 \times \dfrac{\pi}{8}=\dfrac{\pi}{4}$

$\triangle OBC \ \ に余弦定理を用いて$
\begin{eqnarray*} BC^2 &=&OB^2+OC^2-2OB \cdot OC \cdot \cos \angle BOC\\ \\ &=&1^2+1^2-2 \times 1 \times 1 \times \cos \dfrac{\pi}{4}\\ \\ &=&2-2 \times \dfrac{\sqrt{2}}{2}\\ \\ &=&2-\sqrt{2} \end{eqnarray*} $\therefore \ \ BC=\sqrt{2-\sqrt{2}}$


(3)

　

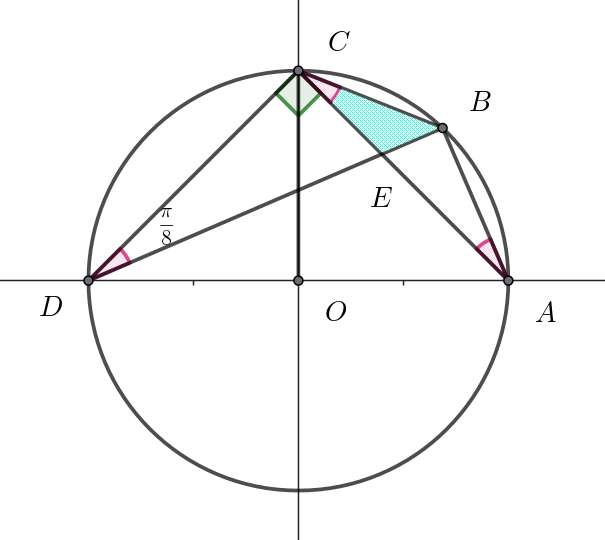
$\triangle CDE \ \ において \quad \angle ACD=\dfrac{\pi}{2},\quad \angle CDE=\dfrac{\pi}{8},\quad CD=\sqrt{2} \quad だから$

$CE=CD\tan \dfrac{\pi}{8}=\sqrt{2}\tan \dfrac{\pi}{8}$
\begin{eqnarray*} \triangle BCE &=&\dfrac{1}{2} \times BC \times CE \times \sin \angle BCE\\ \\ &=&\dfrac{1}{2} \times \sqrt{2-\sqrt{2}} \times \sqrt{2}\tan \dfrac{\pi}{8} \times \sin \dfrac{\pi}{8}\\ \\ &=&\dfrac{\sqrt{2}}{2} \sqrt{2-\sqrt{2}} \times \dfrac{\sin ^2 \dfrac{\pi}{8} }{\cos \dfrac{\pi}{8}}\\ \end{eqnarray*} $ここで$

$\sin ^2 \dfrac{\pi}{8}=\dfrac{1}{2}(1-\cos \dfrac{\pi}{4})=\dfrac{1}{2}(1-\dfrac{\sqrt{2}}{2})=\dfrac{2-\sqrt{2}}{4}$

$\cos ^2 \dfrac{\pi}{8}=\dfrac{1}{2}(1+\cos \dfrac{\pi}{4})=\dfrac{1}{2}(1+\dfrac{\sqrt{2}}{2})=\dfrac{2+\sqrt{2}}{4}$

\begin{eqnarray*} \triangle BCE &=&\dfrac{\sqrt{2}}{2} \sqrt{2-\sqrt{2}} \times \dfrac{\dfrac{2-\sqrt{2}}{4}}{\dfrac{\sqrt{2+\sqrt{2}}}{2}}\\ \\ &=&\dfrac{\sqrt{2}}{4} \sqrt{2-\sqrt{2}} \times \dfrac{(2-\sqrt{2})\sqrt{2+\sqrt{2}}}{2+\sqrt{2}}\\ \\ &=&\dfrac{\sqrt{2}}{4} \times \dfrac{2-\sqrt{2}}{2+\sqrt{2}} \times \sqrt{(2-\sqrt{2})(2+\sqrt{2})}\\ \\ &=&\dfrac{\sqrt{2}}{4} \times \dfrac{(2-\sqrt{2})^2}{4-2} \times \sqrt{4-2}\\ \\ &=&\dfrac{1}{4} \times (6-4\sqrt{2})\\ \\ &=&\dfrac{3-2\sqrt{2}}{2} \end{eqnarray*}

ページの先頭へ↑



メインメニュー　に戻る