九州大学(理系) 2025年 問題1
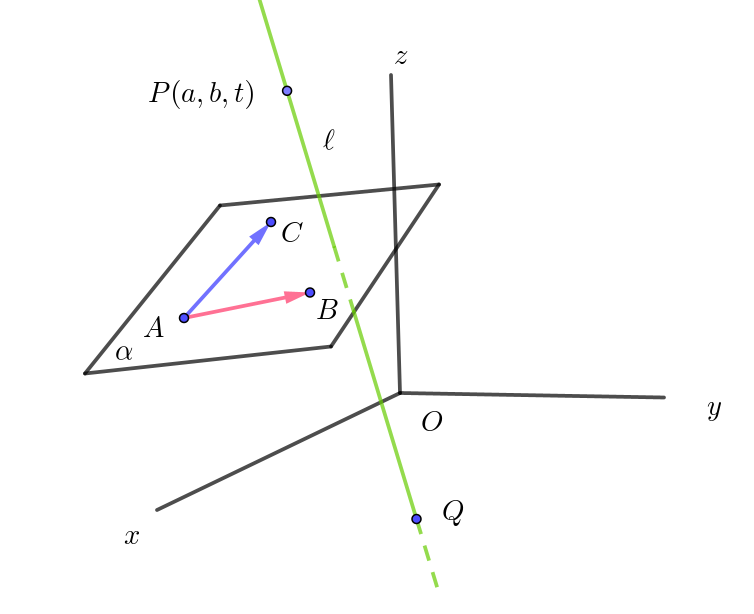
$座標空間内の \ 3\ 点A(1,\ 1,\ -5),\ \ B(-1,\ -1,\ 7),\ \ C(1,\ -1,\ 3)\ を通る平面を \ \alpha \ とする。点P(a,\ b,\ t)\ を$
$通り \ \alpha \ に垂直な直線と \ xy\ 平面との交点を \ Q\ とする。$
$(1)\ \ 点Q\ の座標を求めよ。$
$(2)\ \ t\ がすべての実数値をとって変化するときの \ OQ\ の最小値が \ 1\ 以下となるような \ a,\ b\ の条件を求めよ。$
$\quad ただし、O\ は原点である。$
(1)
$\vec{AC}=\vec{OC}-\vec{OA}=(1,\ -1,\ 3)-(1,\ 1,\ -5)=(0,\ -2,\ 8)$
$点P(a,\ b,\ t)\ を通り \ \alpha \ に垂直な直線を \ \ell \ とし、Q(x,\ y,\ 0)\quad とおくと$
$\vec{PQ}=\vec{OQ}-\vec{OP}=(x,\ y,\ 0) - (a,\ b,\ t)=(x-a,\ y-b,\ -t)$
$\ell \perp \alpha \quad だから \quad \ell \perp \vec{AB},\quad \ell \perp \vec{AC}$
(i)$\ \ \ell \perp \vec{AB}\quad より \quad \vec{PQ} \cdot \vec{AB}=0$
$\quad -2(x-a)-2(y-b)+12(-t)=0$
$\quad (x-a) + (y-b)+6t=0 \hspace{5em}①$
(ii)$\ \ \ell \perp \vec{AC} \quad より \quad \vec{PQ} \cdot \vec{AC}=0$
$\quad -2(y-b)+8(-t)=0$
$\quad y=b-4t $
$①に代入して$
$x=a + b -6t-(b-4t)=a-2t$
$よって \quad Q(a-2t,\ b-4t,\ 0)$
(2)
\begin{eqnarray*} OQ^2 &=&(a-2t)^2+(b-4t)^2\\ \\ &=&20t^2-4(a+2b)t+a^2+b^2\\ \\ &=&20\big(t^2-\dfrac{a+2b}{5}t\big)+a^2+b^2\\ \\ &=&20\big(t-\dfrac{a+2b}{10}\big)^2+a^2+b^2 - \dfrac{20(a+2b)^2}{100}\\ \\ &=&20\big(t-\dfrac{a+2b}{10}\big)^2+\dfrac{1}{5}(4a^2+b^2-4ab)\\ \\ &=&20\big(t-\dfrac{a+2b}{10}\big)^2+\dfrac{1}{5}(2a-b)^2\\ \end{eqnarray*}
$OQ^2 \ \ は \ \ t=\dfrac{a+2b}{10} \ \ のとき最小値 \ \ \dfrac{1}{5}(2a-b)^2 \ \ をもつから$
$OQ\ の最小値が \ 1\ 以下となるような \ a,\ b\ の条件は$
$\dfrac{1}{5}(2a-b)^2 \leqq 1$
$(2a-b)^2 \leqq 5$
$-\sqrt{5} \leqq 2a-b \leqq \sqrt{5}$
メインメニュー に戻る