京都大学(理系) 2024年 問題5
$a\ は\ \ a \geqq 1\ \ を満たす定数とする。座標平面上で、次の \ 4\ つの不等式が表す領域を \ D_a \ とする。$
$\hspace{3em} x \geqq 0,\quad \cfrac{e^x-e^{-x}}{2} \leqq y , \quad y \leqq \cfrac{e^x+e^{-x}}{2} , \quad y \leqq a$
$次の問いに答えよ。$
$(1)\ \ D_a \ の面積 \ S_a\ を求めよ。$
\[(2)\ \ \lim_{a \rightarrow \infty} S_a \ \ を求めよ。\]
(1)
(i)$\ \ y=\cfrac{e^x+e^{-x}}{2}\ \ について$
$\quad y'=\cfrac{e^x-e^{-x}}{2} \ \ より \ \ x > 0\ \ のとき \ \ y' > 0 \ \ だから単調増加で、x=0 \ のとき \ y=1$
(ii)$\ \ y=\cfrac{e^x-e^{-x}}{2}\ \ について$
$\quad y'=\cfrac{e^x+e^{-x}}{2} > 0 \ \ だから単調増加、 x=0 \ \ のとき \ \ y=0$
(iii)$\ \ \cfrac{e^x+e^{-x}}{2} > \cfrac{e^x-e^{-x}}{2} \quad だからグラフの位置関係は右図のとおり$
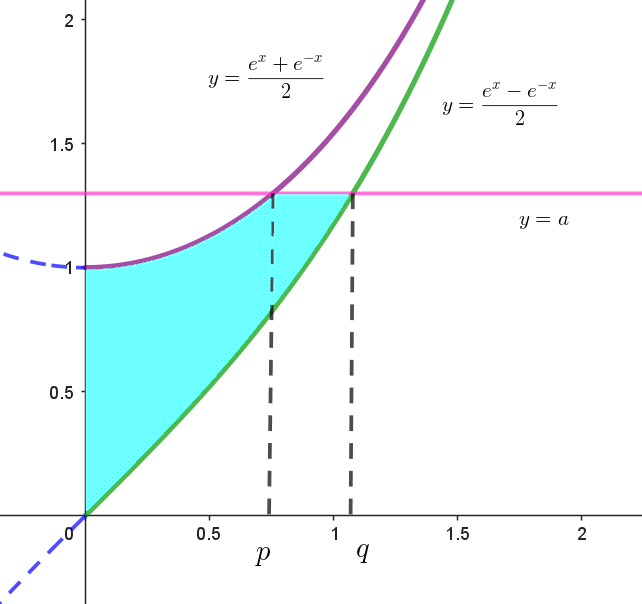
(iv)$\ \ y=\cfrac{e^x+e^{-x}}{2} \ \ と \ \ y=a \ \ の交点は$
$\quad \cfrac{e^x+e^{-x}}{2}=a$
$\quad e^x-2a+e^{-x}=0$
$\quad e^{2x}-2ae^x+1=0$
$\quad e^x=a \pm \sqrt{a^2-1}$
$\quad e^x=a + \sqrt{a^2-1} \ \ を満たす \ x\ を \ p\ とおくと \quad p=\log(a+\sqrt{a^2-1})$
$\qquad e^p=a+\sqrt{a^2-1},\qquad e^{-p}=\cfrac{1}{a+\sqrt{a^2-1}}=a-\sqrt{a^2-1}$
$\quad e^x=a-\sqrt{a^2-1} \ \ は$
$\qquad x=\log(a-\sqrt{a^2-1})=\log \dfrac{a^2-(a^2-1)}{a+\sqrt{a^2-1}}=\log \dfrac{1}{a+\sqrt{a^2-1}}=-\log(a+\sqrt{a^2-1})< 0$
(v)$\ \ y=\cfrac{e^x -e^{-x}}{2}\ \ と \ y=a\ の交点は$
$\quad \cfrac{e^x -e^{-x}}{2}=a$
$\quad e^x-2a-e^{-x}=0$
$\quad e^{2x}-2ae^x-1=0$
$\quad e^x=a \pm \sqrt{a^2+1}$
$\quad e^x=a + \sqrt{a^2+1}\ \ を満たす \ x\ を \ q\ とおくと \quad q=\log(a+\sqrt{a^2+1})$
$\qquad e^q=a+\sqrt{a^2+1},\qquad e^{-q}=\cfrac{1}{a+\sqrt{a^2+1}}=-a+\sqrt{a^2+1}$
$\quad e^x=a-\sqrt{a^2+1} \ \ については、右辺は明らかに負だから満たす \ x\ はない$
$したがって$
\begin{eqnarray*}
S_a
&=&\int_0^q(a-\dfrac{e^x-e^{-x}}{2})dx- \int_0^p(a-\dfrac{e^x+e^{-x}}{2})dx\\
\\
&=&\big[ax-\dfrac{e^x+e^{-x}}{2}\big]_0^q- \big[ax-\dfrac{e^x-e^{-x}}{2}\big]_0^p\\
\\
&=&aq-\dfrac{e^q+e^{-q}}{2}+1-(ap-\dfrac{e^p-e^{-p}}{2})\\
\\
&=&a(q-p)-\dfrac{e^q+e^{-q}}{2}+\dfrac{e^p-e^{-p}}{2}+1\\
\\
&=&a(\log(a+\sqrt{a^2+1})-\log(a+\sqrt{a^2-1}))-\dfrac{a+\sqrt{a^2+1}+(-a+\sqrt{a^2+1})}{2}+\dfrac{a+\sqrt{a^2-1}-(a-\sqrt{a^2-1})}{2}+1\\
\\
&=&a(\log(a+\sqrt{a^2+1})-\log(a+\sqrt{a^2-1}))-\sqrt{a^2+1}+\sqrt{a^2-1} +1\\
\end{eqnarray*}
(2)
(i)$\ \ T_a=a\{\log(a+\sqrt{a^2+1})-\log(a+\sqrt{a^2-1})\} \quad とおくと$
\begin{eqnarray*} \quad T_a &=&a\big\{\log a(1+\dfrac{\sqrt{a^2+1}}{a})-\log a(1+\dfrac{\sqrt{a^2-1}}{a})\big\}\\ \\ &=&a\big\{\log (1+\dfrac{\sqrt{a^2+1}}{a})-\log (1+\dfrac{\sqrt{a^2-1}}{a})\big\}\\ \\ &=&a\big\{\log (1+\sqrt{1+\dfrac{1}{a^2}})-\log (1+\sqrt{1-\dfrac{1}{a^2}})\big\}\\ \end{eqnarray*} $\quad \cfrac{1}{a^2}=b \quad とおくと$
$\quad T_a=\cfrac{1}{\sqrt{b}} \big\{\log (1+\sqrt{1+b})-\log (1+\sqrt{1-b})\big\}$
$\quad f(x)=\log (1+\sqrt{1+x}) \quad とおくと \quad f'(x)=\cfrac{1}{1+\sqrt{1+x}} \times \cfrac{1}{2\sqrt{1+x}}$
\begin{eqnarray*} \quad T_a &=&\cfrac{1}{\sqrt{b}} \big\{f(b)-f(-b)\big\}\\ \\ &=&\cfrac{1}{\sqrt{b}} \times \cfrac{f(b)-f(-b)}{b-(-b)} \times 2b\\ \\ &=&2\sqrt{b} \times \cfrac{f(b)-f(-b)}{b-(-b)}\\ \end{eqnarray*}
$\quad 平均値の定理より \quad \cfrac{f(b)-f(-b)}{b-(-b)}=f'(c) \ \ (-b < c < b )\ \ を満たす \ c\ が存在する。$
$\quad a \longrightarrow \infty \ \ のとき \ \ b \longrightarrow 0 \quad したがって、はさみうちの原理より \quad c \longrightarrow 0 \quad だから$
$\quad T_a=2\sqrt{b} f'(c) =2\sqrt{b} \times \cfrac{1}{1+\sqrt{1+c}} \times \cfrac{1}{2\sqrt{1+c}} \longrightarrow 0$
(ii)$\ \ U_a=\sqrt{a^2-1}-\sqrt{a^2+1} \quad とおくと$
$\quad U_a=\cfrac{(a^2-1)-(a^2+1)}{\sqrt{a^2-1}+\sqrt{a^2+1}}=\cfrac{-2}{\sqrt{a^2-1}+\sqrt{a^2+1}}$
$\quad a \longrightarrow \infty \quad のとき \quad U_a \longrightarrow 0$
\[以上より\quad \lim_{a \rightarrow \infty} S_a=1\]
$(研究)$
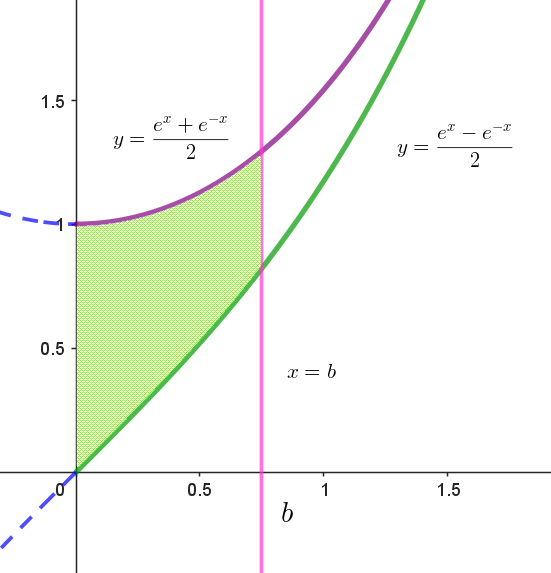
$y=a \ \ の代わりに \ \ x=b\ \ (>0)\ \ とすると$
\begin{eqnarray*}
S_b
&=&\int_0^b\big(\dfrac{e^x+e^{-x}}{2} - \dfrac{e^x-e^{-x}}{2}\big)dx\\
\\
&=&\int_0^b e^{-x} dx\\
\\
&=&\big[-e^{-x}\big]_0^b\\
\\
&=&1-e^{-b}
\end{eqnarray*}
\[したがって \quad \ \lim_{b \rightarrow \infty} S_b=1\]
$これでは簡単すぎるから \ \ y=a\ \ としたのでしょうか$
メインメニュー に戻る