MY MATH NOTE

京都大学(理系) 2018年　問題3

$\alpha \ は \ \ 0 < \alpha \leqq \cfrac{\pi}{2}\ \ を満たす定数とし、四角形 \ ABCD\ に関する次の \ 2\ つの条件を考える。$
(i)$\ \ 四角形 \ ABCD\ は半径 \ 1\ の円に内接する。$
(ii)$\ \ \angle ABC =\angle DAB=\alpha　$
$条件$(i)$と$(ii)$を満たす四角形のなかで、4\ 辺の長さの積 \ \ k=AB\cdot BC\cdot CD\cdot DA \ \ が最大となるもの$
$についてk\ の値を求めよ。$

　
$(1)$

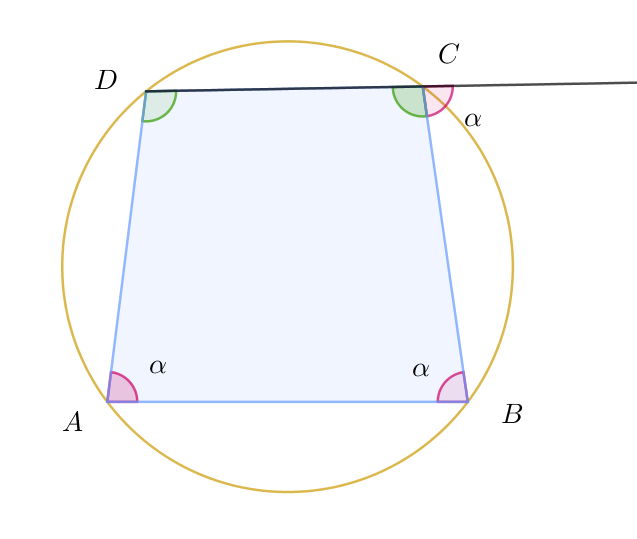
$四角形 \ ABCD\ は円に内接するから、向かい合う内角の和は \ 180°$
$よって \quad \angle BCD = 180°-\angle A=180°-\alpha $
$\angle Cの外角=180°-\angle BCD=\alpha $
$よって \quad \angle ABC=\angle C の外角=\alpha $
$錯角が等しいので \quad AB /\!/DC$

　
$(2)$

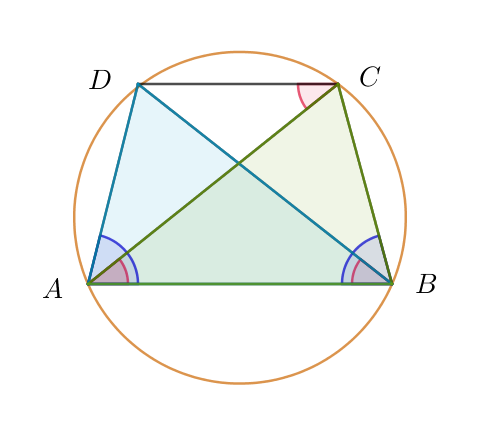
$\triangle ABC \ \ と \ \ \triangle BAD \ \ において$

$仮定より \quad \angle ABC=\angle BAD=\alpha \hspace{9em}①$

$円周角の定理より \quad \angle ABD=\angle ACD $
$(1)より \quad AB /\!/DC だから \quad \angle ACD=\angle BAC$
$よって \quad \angle ABD =\angle BAC \hspace{12em}②$

$ABは共通　\hspace{18em}③$

$①、②、③より \ 1\ 辺と両端角が等しいので \quad \triangle ABC \equiv \triangle BAD$
$よって \quad BC=AD$

$したがって、四角形 \ ABCD\ は等脚台形である。$


$(3)$

　
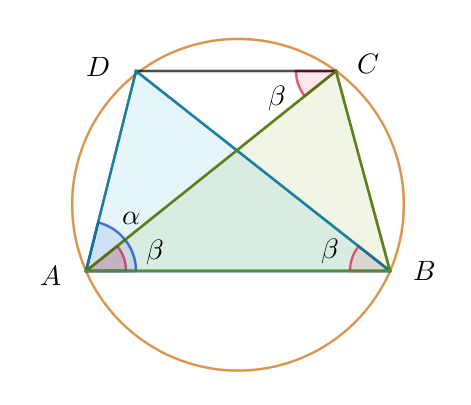
$\angle ABD=\beta \quad とおくと$

$\triangle ABD に正弦定理を用いて \quad \cfrac{AB}{\sin (180°-\alpha -\beta )}=\cfrac{DA}{\sin \beta }=2$

$\triangle ACD に正弦定理を用いて \quad \cfrac{CD}{\sin (\alpha -\beta )}=2$

$よって$

$\qquad AB=2\sin (180°-\alpha -\beta)=2\sin(\alpha +\beta)$

$\qquad BC=DA=2\sin \beta$

$\qquad CD=2\sin(\alpha -\beta)$

\begin{eqnarray*} k &=&AB\cdot BC\cdot CD\cdot DA\\ \\ &=&2\sin(\alpha +\beta) \times 2\sin \beta \times 2\sin(\alpha -\beta) \times 2\sin \beta\\ \\ &=&16\sin ^2 \beta \sin(\alpha +\beta) \sin(\alpha -\beta)\\ \\ &=&-8\sin ^2 \beta (\cos 2\alpha - \cos 2\beta)\\ \\ &=&-4(1-\cos 2\beta )(\cos 2\alpha - \cos 2\beta)\\ \\ &=&-4\{\cos ^2 2\beta -(1+\cos 2\alpha )\cos 2\beta +\cos 2\alpha \}\\ \\ &=&-4\{\cos ^2 2\beta -2\cos ^2\alpha \ \cos 2\beta +2\cos ^2\alpha -1\}\\ \\ &=&-4\{(\cos 2\beta -\cos ^2\alpha )^2 -\cos ^4\alpha +2\cos ^2\alpha -1\}\\ \\ &=&-4\{(\cos 2\beta -\cos ^2\alpha )^2 -(1-\cos ^2\alpha )^2\}\\ \\ &=&-4(\cos 2\beta -\cos ^2\alpha )^2 +4\sin ^4\alpha\\ \end{eqnarray*}
$\quad \alpha \ は定数だから \quad \cos 2\beta =\cos ^2 \alpha \quad のとき \ k\ は最大となり、最大値は \quad 4\sin ^4 \alpha $



$(研究)$

$\alpha \ が定数でなく、変数の場合$

$\quad \sin \alpha =1 \quad すなわち \quad \alpha =\cfrac{\pi}{2}=90°\quad のとき \ k\ は最大となる。$
$このとき$
$\quad \cos 2\beta =\cos ^2 \cfrac{\pi}{2}=0 \quad より \quad 2\beta=\cfrac{\pi}{2} \qquad \therefore \ \ \beta=\cfrac{\pi}{4}$

$よって$

$\quad AB=2\sin (\alpha +\beta)=2\sin(\cfrac{\pi}{2}+\cfrac{\pi}{4})=2 \times \cfrac{\sqrt{2}}{2}=\sqrt{2}$

$\quad BC=2\sin \beta=2\sin \cfrac{\pi}{4}=\sqrt{2}$

$\quad \angle A=90°,\quad AB=BC \quad だから\ \ 四角形 \ ABCD\ は正方形となる。$


$さらに、次のような方法も考えられます。$

$相加平均・相乗平均の不等式をつかって$

$\sqrt[4]{AB\cdot BC\cdot CD\cdot DA} \ \ \leqq \cfrac{AB + BC + CD + DA}{4} \quad より$

$k \leqq \big(\cfrac{AB + BC + CD + DA}{4}\big)^4$

$等号は \quad AB=BC=CD=DA \quad のときだから、四角形 \ ABCD\ は正方形となる。$

$このとき \quad AC=円の直径=2 \quad より \quad 　AB=\cfrac{AC}{\sqrt{2}}=\sqrt{2}$

$kの最大値は \quad AB^4=(\sqrt{2})^4=4$

ページの先頭へ↑