京都府立医科大学 2024年　問題3


$半径 \ 1\ の円に内接する五角形 \ A_1A_2A_3A_4A_5\ を考える。線分 \ A_1A_4\ と \ A_2A_5\ の交点を \ B\ とし、\triangle A_1A_2B\ は$
$正三角形であるとする。また、A_3A_2=A_3A_4 \ とする。a=A_1A_2,\ \ b=A_4A_5\ \ とおく。$
$(1)\ \ 線分 \ A_3B \ の長さを求めよ。$
$(2)\ \ b\ を \ a\ を用いて表せ。$
$(3)\ \ 五角形 \ A_1A_2A_3A_4A_5\ の面積 \ S\ を \ a\ を用いて表し、S\ の最大値を求めよ。$


(1)



$A_3A_2=A_3A_4 =c \ \ とおくと$

(i)$\ \ 弧A_2A_3=弧A_3A_4 \ \ だから円周角の定理より \quad \angle A_2A_1A_3=\angle A_3A_1A_4=\theta \ \ とおく$

$\quad \triangle A_1A_2B\ は正三角形だから \quad \angle A_2A_1A_4=60°$

$ \quad 2\theta =60° \quad より \ \ \theta=30°$

　

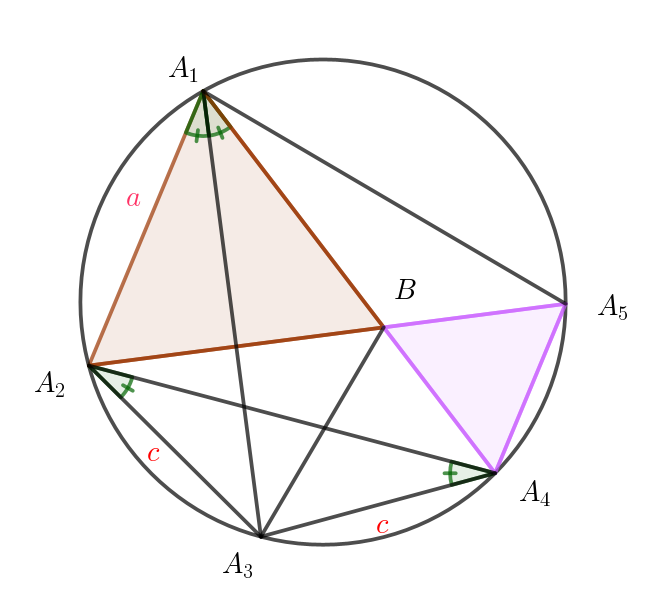
(ii)$ \ \ \triangle A_2A_3A_4 \ は\ A_3A_2=A_3A_4 \ の二等辺三角形だから$

$\quad \angle A_3A_2A_4=\angle A_3A_4A_2$

$\quad 円周角の定理より$

$\quad \angle A_2A_4A_3 =\angle A_2A_1A_3=\theta ,\quad \angle A_3A_2A_4 =\angle A_3A_1A_4=\theta$

$\triangle A_2A_3A_4 において$

$外接円の半径は \ 1\ だから正弦定理を用いて$

$\cfrac{A_2A_3}{\sin 30°}=2 \times 1$

$c=A_2A_3=2 \times \sin 30°=1$

$\triangle A_1A_2A_3 と \triangle A_1BA_3 において$

$A_1A_2=A_1B,\quad A_1A_3 は共通, \quad \angle A_2A_1A_3 =\angle BA_1A_3$

$したがって　\quad \triangle A_1A_2A_3 \equiv \triangle A_1BA_3 $

$よって \quad A_3B=A_3A_2=c=1$


(2)

　

$\angle A_2A_3A_4 =180°- 2\theta=120°$

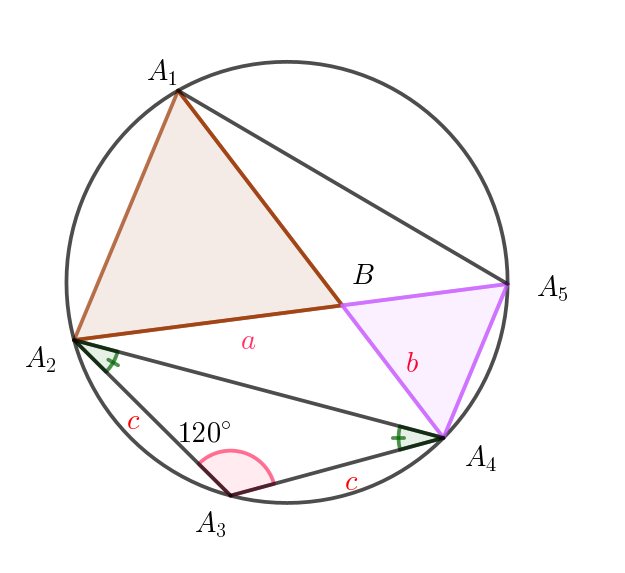
$\triangle A_2A_3A_4 \ \ に余弦定理を用いて$

$A_2A_4^2=c^2+c^2-2c^2\cos 120°=2c^2-2c^2 \times (-\dfrac{1}{2})=3c^2=3$

$また$

$\angle A_2BA_4 =180°- \angle A_1BA_2=180 °- 60°=120°$

$\triangle A_2A_3A_4 \ \ に余弦定理を用いて$

$A_2A_4^2=a^2+b^2-2ab\cos 120°=a^2+b^2-2ab \times (-\dfrac{1}{2})=a^2+b^2+ab$

$\therefore \ \ a^2+b^2+ab=3$

$b^2+ab+a^2-3=0$

$b=\cfrac{-a+\sqrt{a^2-4(a^2-3)}}{2}=\cfrac{\sqrt{12-3a^2}-a}{2}$


(3)

　

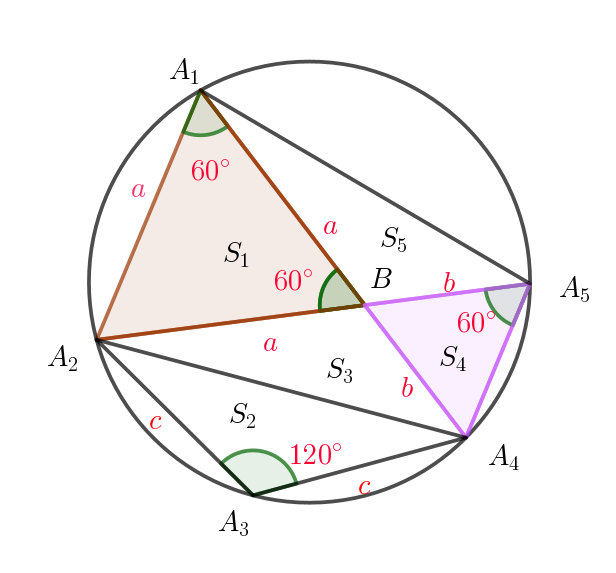
$S_1=\triangle A_1A_2B=\cfrac{1}{2}a^2\sin 60°=\cfrac{\sqrt{3}}{4} a^2 $

$S_2=\triangle A_2A_3A_4=\cfrac{1}{2}c^2\sin 120°=\cfrac{\sqrt{3}}{4}$

$S_3=\triangle A_2A_4B=\cfrac{1}{2}ab\sin 120°=\cfrac{\sqrt{3}}{4}ab$

$\triangle A_4A_5B\ において$

$円周角の定理より \quad \angle A_2A_5A_4=\angle A_2A_1A_4=60°$

$対頂角は等しいから \quad \angle A_4BA_5= \angle A_1BA_2=60°$

$したがって \quad \triangle A_4A_5B\ は正三角形だから$

$S4=\triangle A_4A_5B=\cfrac{1}{2}b^2\sin 60°=\cfrac{\sqrt{3}}{4} b^2 $

$S_5=\triangle A_1A_5AB=\cfrac{1}{2}ab\sin 120°=\cfrac{\sqrt{3}}{4}ab$

$以上より$
\begin{eqnarray*} S &=&S_1+S_2+S_3+S_4+S_5\\ \\ &=&\cfrac{\sqrt{3}}{4} a^2+ \cfrac{\sqrt{3}}{4} + \cfrac{\sqrt{3}}{4} ab + \cfrac{\sqrt{3}}{4} b^2 + \cfrac{\sqrt{3}}{4} ab\\ \\ &=&\cfrac{\sqrt{3}}{4}( a^2+ b^2+2ab+1) \end{eqnarray*} $(2)より \quad a^2+b^2+ab=3 \quad だから$

$S=\cfrac{\sqrt{3}}{4}( (3-ab)+2ab+1)=\cfrac{\sqrt{3}}{4}( 4+ab)$

$ここで \quad a^2+b^2+ab=3 \ \ より \ \ (a+b)^2=3+ab$

$相加相乗平均の不等式 \ \ a+b \geqq 2\sqrt{ab} \ \ を用いて$

$3+ab \geqq 4ab $

$\therefore ab \leqq 1$

$したがって、五角形 \ A_1A_2A_3A_4A_5\ の面積 \ S\ の最大値は$

$S =\cfrac{\sqrt{3}}{4}( 4+ab)\leqq \cfrac{\sqrt{3}}{4} \times ( 4+ 1)=\cfrac{5\sqrt{3}}{4}$

$ただし等号は\ a=b\ のときだから \quad a^2+a^2+a^2=3 \ \ より \ \ a=1$

$このとき \ \ a=b=1\ \ だから点 \ B\ が円の中心のときである。$


ページの先頭へ↑




メインメニュー　に戻る